Matematika 1 - 3.8 Zbrajanje i oduzimanje algebarskih razlomaka

Najmanji zajednički višekratnik algebarskih izraza

Prisjetite se kako smo određivali najmanji zajednički višekratnik dvaju ili više brojeva. Gdje smo upotrebljavali najmanji zajednički višekratnik?

Najprije smo zadane brojeve rastavili na proste faktore. Za svaki prosti broj koji se pojavljuje u rastavima odredili smo najveći broj pojavljivanja. Toliko će se puta taj prosti broj pojaviti u najmanjemu zajedničkom višekratniku. Najmanji zajednički višekratnik upotrebljavali smo pri zbrajanju razlomaka.

Na sličan način možemo odrediti najmanji zajednički višekratnik algebarskih izraza. Pogledajte animaciju.

Primjer 1.

Odredimo najmanji zajednički višekratnik algebarskih izraza $6 x^{8} y$ i $4 x^{6} y^{7} z^{2} .$

Algebarski su izrazi zapisani u faktoriziranom obliku. Promotrimo redom jednake faktore i njihove potencije: $x^{8}, x^{6}$ zatim $y, y^{7}$ i $z^{2} .$ Za jednake faktore uzmimo potenciju s najvećim eksponentom.

Dobivamo: $x^{8}, y^{7}, z^{2} .$ Odredimo $nzv (6, 4) = 12 .$

Pomnožimo dobivene izraze i broj: $nzv (6 x^{8} y, 4 x^{6} y^{7} z^{2}) = 12 x^{8} y^{7} z^{2} .$

Kolekcija zadataka 1

Zadatak 1.

Uparite algebarske izraze s njihovim najmanjim zajedničkim višekratnikom.

$2 x^{2} - 18, x^{2} + 3 x$	$2 x^{2} {(x + 3)}^{2} (x - 3)$
$2 x^{2} + 6 x, x^{3} - 3 x^{2}$	$2 x^{2} (x + 3) (x - 3)$
$x^{4} + 6 x^{3} + 9 x^{2}, 2 x^{3} - 18 x$	$2 x^{2} (x - 3) (x^{2} + 3 x + 9)$
$x^{3} - 27, 2 x^{3} - 6 x^{2}$	$2 x (x + 3) (x - 3)$

null

Zadatak 2.

Odredite najmanji zajednički višekratnik triju algebarskih izraza. Upišite eksponente na odgovarajuća mjesta.

Zatvori

Primjer 2.

Određivali smo najmanji zajednički višekratnik prirodnih brojeva. Možemo li odrediti najmanji zajednički višekratnik u skupu cijelih brojeva? Koji bi broj bio najmanji višekratnik brojeva $4$ i $- 4 ?$ Najmanji cijeli broj koji je višekratnik brojeva $4$ i $- 4$ ne postoji jer su višekratnici $. . . - 20,$ $- 16,$ $- 12,$ $- 8,$ $- 4,$ $4,$ $8,$ $12 . . .$

Zato ćemo reći da je najmanji zajednički višekratnik dvaju cijelih brojeva najmanji prirodni broj koji je višekratnik jednoga i drugoga broja. Tako je $nzv (- 4, 4) = 4 .$

Odredimo $nzv (x, - x)$ i $nzv (1 - x, - 1 + x) .$ Vidimo da se traži najmanji zajednički višekratnik suprotnih izraza. Ne možemo odrediti koji je od tih izraza pozitivan pa možemo reći da je $nzv (x, - x) = x$ ili $nzv (x, - x) = - x,$ odnosno $nzv (1 - x, - 1 + x) = 1 - x$ ili $nzv (1 - x, - 1 + x) = - 1 + x .$

Zadatak 3.

Odredite $nzv (1 - x^{2}, x^{3} - 1) .$

$1 - x^{2} = (1 - x) (1 + x)$

$x^{3} - 1 = (x - 1) (x^{2} + x + 1)$

Vidimo da se u rastavima na faktore pojavljuju suprotni izrazi $1 - x$ i $x - 1$ pa ćemo u zajednički višekratnik kao faktor uzeti jednog od njih, na primjer $x - 1$ . Zato je:

$nzv (1 - x^{2}, x^{3} - 1) = (x - 1) (x + 1) (x^{2} + x + 1) .$

Zaključimo.

Pri određivanju najmanjega zajedničkog višekratnika algebarskih izraza treba provesti nekoliko koraka:

faktorizirati, to jest rastaviti na faktore algebarske izraze
prema potrebi izlučiti odgovarajuće konstante kako bismo dobili identične algebarske izraze
uočiti iste algebarske izraze i njihove potencije
prepisati sve različite algebarske izraze, a za potenciju uzeti najveću koja se pojavljuje
konstante pomnožiti, a ako su cijeli brojevi, uzeti njihov najmanji zajednički višekratnik.

Zbrajanje i oduzimanje algebarskih razlomaka

U osnovnoj ste školi naučili zbrajati i oduzimati brojevne razlomke. Možemo li na sličan način zbrajati i oduzimati algebarske razlomke? Pogledajte videozapis.

Primjer 3.

Zbrojimo algebarske razlomke

$\frac{7}{2 x - x^{2}} + \frac{4}{x^{2} - 4} + \frac{5}{3 x + 6} .$

Odredimo najmanji zajednički nazivnik.

$2 x - x^{2} = x (2 - x)$

$x^{2} - 4 = (x - 2) (x + 2)$

$3 x + 6 = 3 (x + 2)$

Vidimo da se u rastavima na faktore pojavljuju suprotni izrazi $2 - x$ i $x - 2$ pa ćemo u zajednički višekratnik kao faktor uzeti jednog od njih, na primjer $x - 2 .$ Zato je:

$nzv (2 x - x^{2}, x^{2} - 4, 3 x + 6) = 3 x (x - 2) (x + 2) .$ Odredili smo zajednički nazivnik.

Odredimo izraze kojima proširujemo razlomke.

Nazivnik je prvog razlomka bio $x (2 - x),$ a novi je nazivnik $3 x (x - 2) (x + 2)$

pa prvi razlomak treba proširiti izrazom $\frac{3 x (x - 2) (x + 2)}{x (2 - x)} = - 3 (x + 2) .$

Nazivnik je drugog razlomka bio $(x - 2) (x + 2),$ a novi je nazivnik $3 x (x - 2) (x + 2)$

pa drugi razlomak treba proširiti izrazom $\frac{3 x (x - 2) (x + 2)}{(x - 2) (x + 2)} = 3 x .$

Nazivnik je trećeg razlomka bio $3 (x + 2),$ a novi je nazivnik $3 x (x - 2) (x + 2)$

pa treći razlomak treba proširiti izrazom $\frac{3 x (x - 2) (x + 2)}{3 (x + 2)} = x (x - 2) .$

Zbroj je tada:

$\begin{array}{l} \frac{7}{2 x - x^{2}} + \frac{4}{x^{2} - 4} + \frac{5}{3 x + 6} = \\ \frac{- 7 \cdot 3 (x + 2) + 4 \cdot 3 x + 5 \cdot x (x - 2)}{3 x (x - 2) (x + 2)} = \\ \frac{- 21 x - 42 + 12 x + 5 x^{2} - 10 x}{3 x (x - 2) (x + 2)} = \\ \frac{5 x^{2} - 19 x - 42}{3 x (x - 2) (x + 2)} \end{array} .$

Projekt

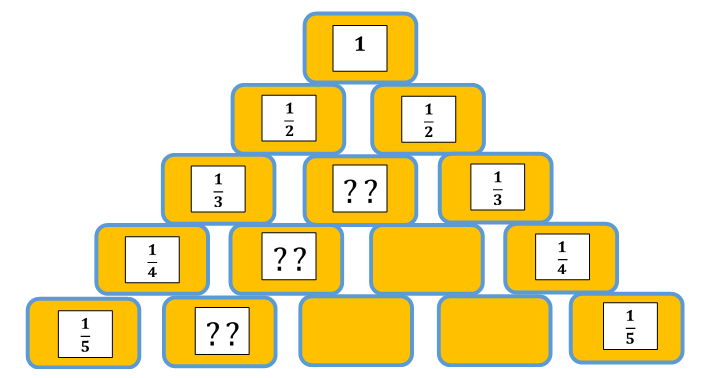
Istražite Leibnizov harmonijski trokut brojeva. Za brojeve $1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4} . . .$ kažemo da se nalaze na prvoj dijagonali Leibnizova trokuta. Svaki je od njih zbroj dvaju brojeva koji se nalaze neposredno ispod njega.

Izračunajte brojeve koji se nalaze u prvih nekoliko redova Leibnizova trokuta.

Druga dijagonala Leibnizova trokuta počinje brojem $\frac{1}{2} .$ Istražite kojeg je oblika broj koji se nalazi u $n$ -tom redu trokuta na drugoj dijagonali.

Treća dijagonala Leibnizova trokuta počinje brojem $\frac{1}{3} .$ Istražite kojeg je oblika broj koji se nalazi u $n$ -tom redu trokuta na trećoj dijagonali. Dokažite da se svi brojevi na trećoj dijagonali mogu zapisati u obliku razlomka s brojnikom 1.

Kutak za znatiželjne

Dokažite jednakosti.

$\frac{16}{1 + a^{16}} + \frac{8}{1 + a^{8}} + \frac{4}{1 + a^{4}} + \frac{2}{1 + a^{2}} + \frac{1}{1 + a} + \frac{1}{1 - a} = \frac{32}{1 - a^{32}}$
$\frac{a^{3}}{(a - b) (a - c)} + \frac{b^{3}}{(b - c) (b - a)} + \frac{c^{3}}{(c - a) (c - b)} = a + b + c$

...i na kraju

Izračunajte i zapišite rješenja u obliku potpuno skraćenog razlomka.

$\frac{1}{3} + \frac{1}{15} = \frac{m}{n},$ $m =$ $n =$ .

null

null
$\frac{2}{5} + \frac{1}{35} = \frac{m}{n},$ $m =$ $n =$ .

null

null
$\frac{3}{7} + \frac{1}{63} = \frac{m}{n},$ $m =$ $n =$ .

null

null

Zadatak 8.

Promotrite niz pribrojnika i rješenja u prethodnom zadatku. Uočavate li pravilnost?

Ako bismo nastavili na isti način, koji bi bio sljedeći zadatak? A rješenje?

Zapišite deseti zadatak i njegovo rješenje pa provjerite jeste li dobro pretpostavili.

Zapišite $n$ -ti zadatak i njegovo rješenje. Provjerite jeste li dobro pretpostavili.

Sljedeći bi zadatak bio $\frac{4}{9} + \frac{1}{99},$ a njegovo je rješenje $\frac{5}{11} .$

Deseti bi zadatak bio $\begin{array}{l} \frac{10}{2 \cdot 10 + 1} + \frac{1}{(2 \cdot 10 + 1) (2 \cdot 10 + 3)} = \frac{10}{21} + \frac{1}{483} \end{array},$ a rješenje $\frac{10 + 1}{2 \cdot 10 + 3} = \frac{11}{23} .$

$n$ -ti zadatak je $\frac{n}{2 n + 1} + \frac{1}{(2 n + 1) (2 n + 3)}$ i njegovo rješenje $\frac{n + 1}{2 n + 3} .$

Provjera:

$\frac{n}{2 n + 1} + \frac{1}{(2 n + 1) (2 n + 3)} = \frac{n (2 n + 3) + 1}{(2 n + 1) (2 n + 3)} = \frac{2 n^{2} + 3 n + 1}{(2 n + 1) (2 n + 3)} = \frac{(2 n + 1) (n + 1)}{(2 n + 1) (2 n + 3)} = \frac{n + 1}{2 n + 3} .$

$\frac{3}{a^{3}} + \frac{1 - 2 a}{a^{2}} =$	$\frac{2 a^{2} - a + 3}{a^{3}}$
$\frac{a - 1}{12} + \frac{a + 1}{10} =$	$\frac{11 a + 1}{60}$
$\frac{a - 1}{12} - \frac{a + 1}{10} =$	$\frac{- 2 a^{2} + a + 3}{a^{3}}$
$\frac{3}{a^{3}} - \frac{1 - 2 a}{a^{2}} =$	$\frac{- a - 11}{60}$

$\frac{3}{a^{2} - 25} + \frac{2}{a^{2} + 5 a} =$	$\frac{a + 4}{6 (a - 3)}$
$\frac{3}{a^{2} - 25} - \frac{2}{a^{2} + 5 a} =$	$\frac{5 a - 4}{6 (a - 3)}$
$\frac{a}{2 a - 6} + \frac{a - 2}{3 a - 9} =$	$\frac{a + 10}{a (a - 5) (a + 5)}$
$\frac{a}{2 a - 6} - \frac{a - 2}{3 a - 9} =$	$\frac{5 a - 10}{a (a - 5) (a + 5)}$

$\frac{1}{1 - 3 a + 9 a^{2}} - \frac{1}{1 + 27 a^{3}} - \frac{1}{1 + 6 a + 9 a^{2}} =$	$\frac{12 x^{2}}{(3 x + 1) {(3 x - 1)}^{2}}$
$\frac{2 x}{9 x^{2} - 1} - \frac{2 x}{9 x^{2} - 6 x + 1} =$	$\frac{- 4 x}{(3 x + 1) {(3 x - 1)}^{2}}$
$\frac{2 x}{9 x^{2} - 1} + \frac{2 x}{9 x^{2} - 6 x + 1} =$	$\frac{6 a - 1}{(1 - 3 a + 9 a^{2}) {(1 + 3 a)}^{2}}$
$\frac{1}{3 a - 1} - \frac{1}{1 + 3 a + 9 a^{2}} + \frac{9 a^{2} + 6 a}{1 - 27 a^{3}} =$	$- \frac{2}{1 + 3 a + 9 a^{2}}$

3.8 Zbrajanje i oduzimanje algebarskih razlomaka

Na početku...

Najmanji zajednički višekratnik algebarskih izraza

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zadatak 3.

Zbrajanje i oduzimanje algebarskih razlomaka

Kolekcija zadataka 2

Zadatak 4.

Zadatak 5.

Kolekcija zadataka 3

Zadatak 6.

Zadatak 7.

Projekt

Kutak za znatiželjne

...i na kraju

Zadatak 8.

3.9 Računanje s algebarskim razlomcima