


Trokut Sierpinskoga jest fraktal koji je opisao Waclaw Franciszek Sierpinski. Sastoji se od jednakostraničnih trokuta.
Pogledajmo korake nastajanja trokuta Sierpinskoga.
Treći korak ponavljamo.
Istražite pravilnosti u trokutu Sierpinskoga. Odgovorite na pitanja:
Povežite slike i pojmove.
Označite točane odgovore.
Ako je onda je
Ako je
onda je
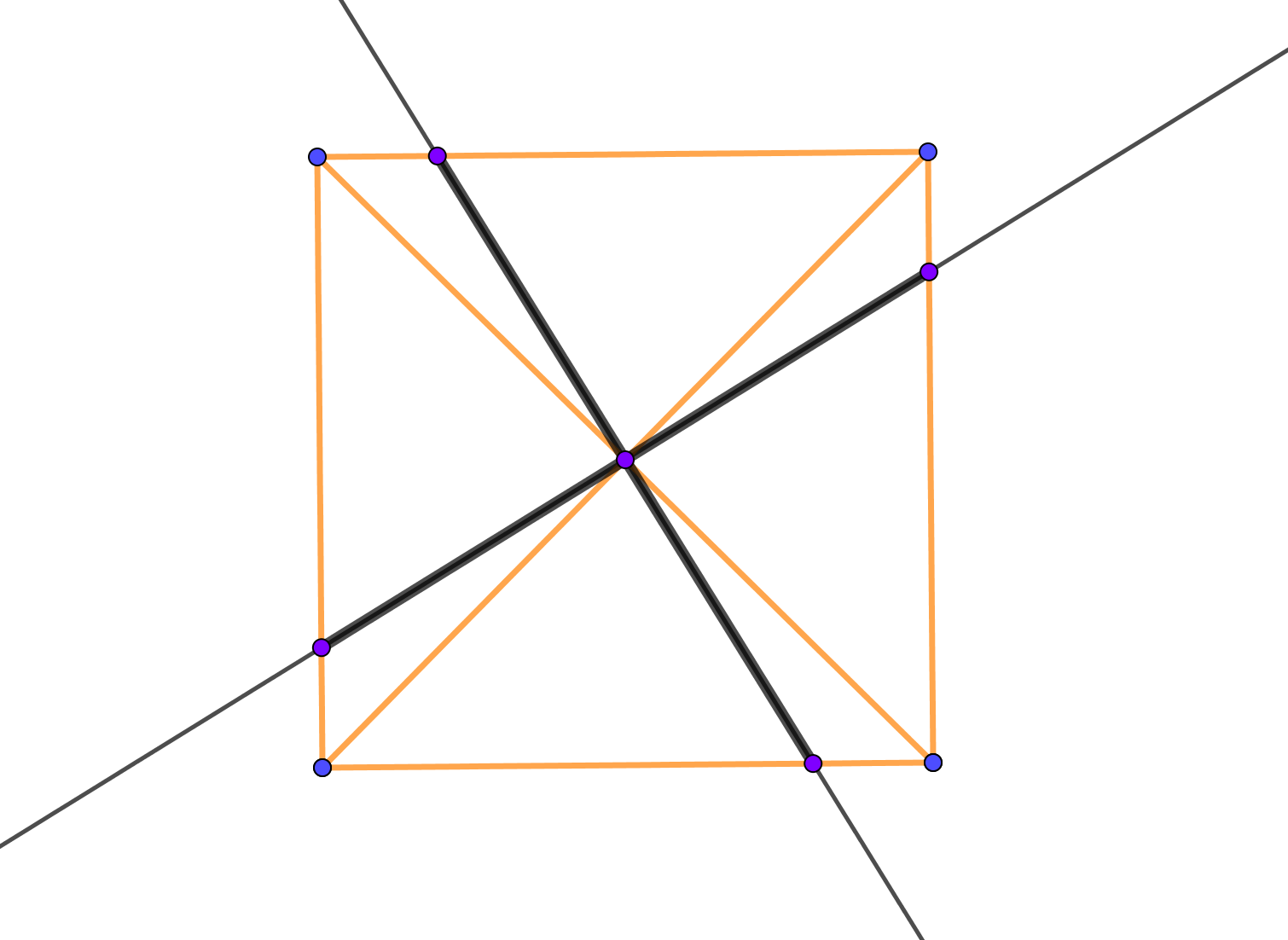
Središtem kvadrata konstruirana su dva okomita pravca. Dokažite da su odsječci tih pravaca unutar kvadrata jednakih duljina.
U pravokutnom trokutu
s pravim kutom u vrhu
konstruirana je srednjica
paralelna sa stranicom
Izračunajte površinu trapeza
ako je
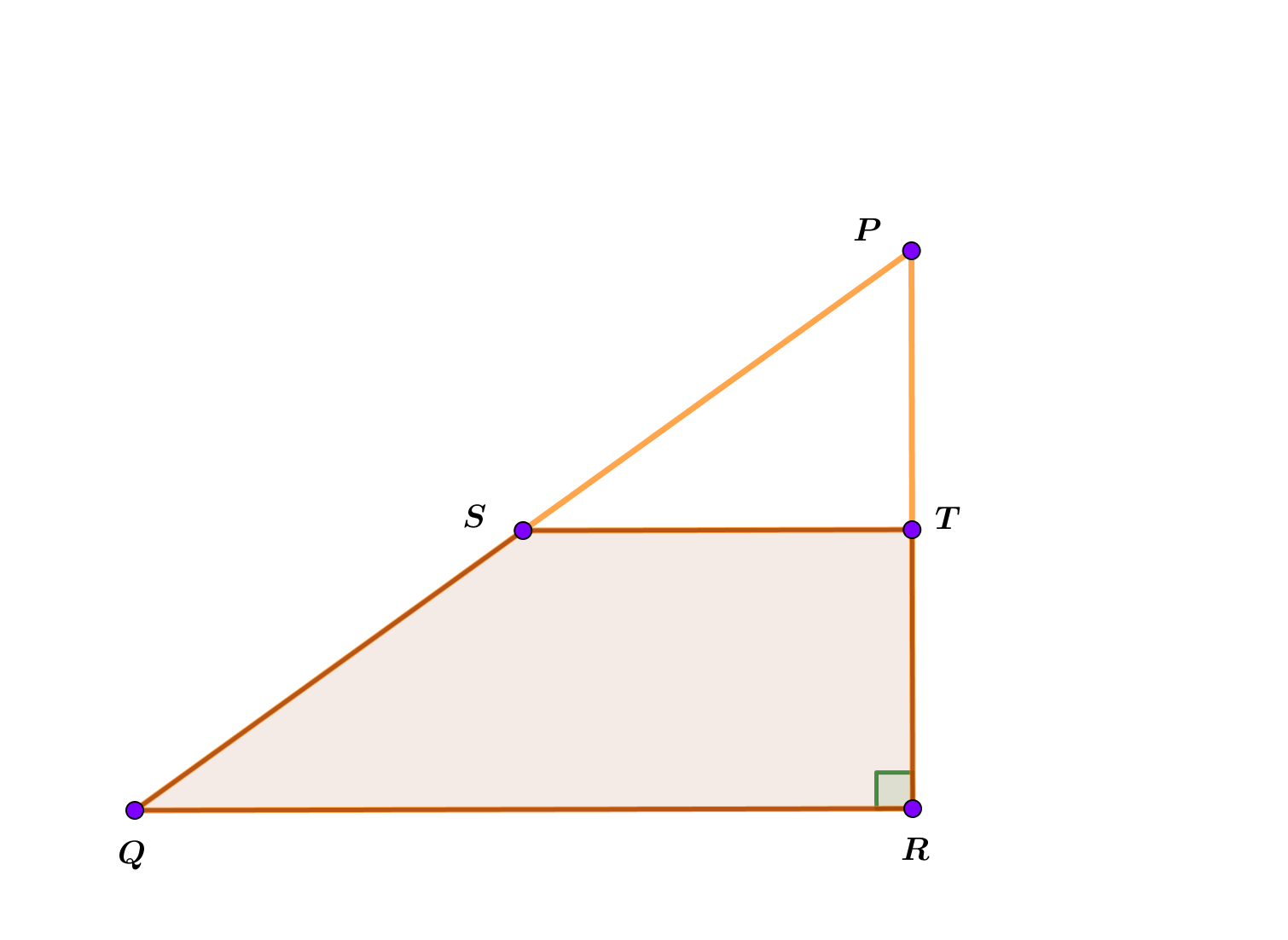
Površina je
Zadatak možemo riješiti na više načina:

Krojačica želi iskoristiti ostatak platna trokutastog oblika kako bi napravila okrugli stolnjak što većeg promjera. Dimenzije platna iznose
i
Promjer okruglog stola za koji želi izraditi stolnjak jest
Hoće li moći izraditi dovoljno velik stolnjak?
Treba izračunati polumjer trokutu upisane kružnice. Površinu trokuta izrazimo na dva načina: Heronovom formulom i formulom za površinu trokuta pomoću polumjera upisane kružnice.
Krojačica će moći izraditi dovoljno velik stolnjak.
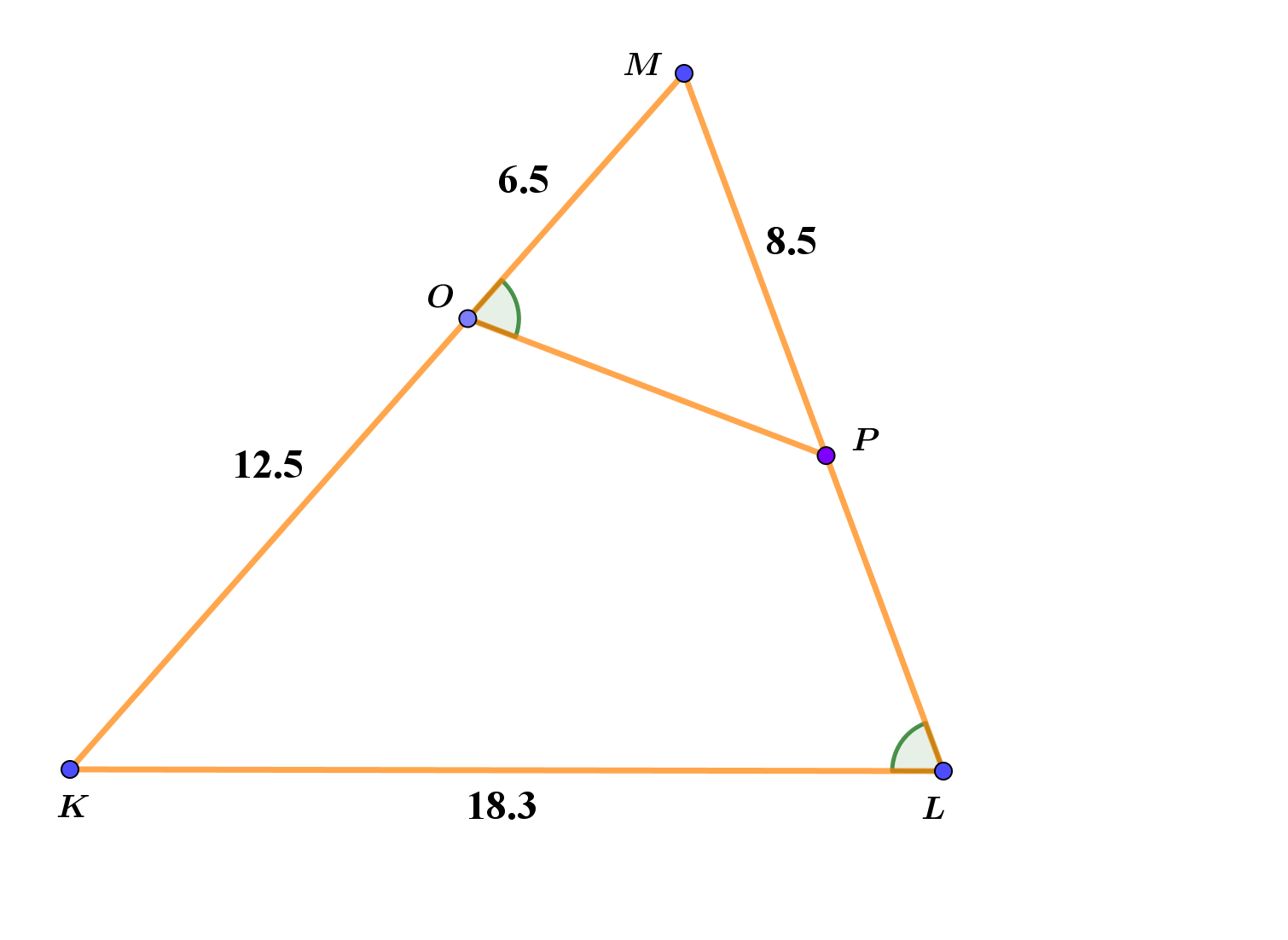
Promotrite sliku pa odgovorite na pitanja.
Trokuti i sukladni su.
Trokuti i slični su.
Odgovarajući elementi trokuta
i
jesu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
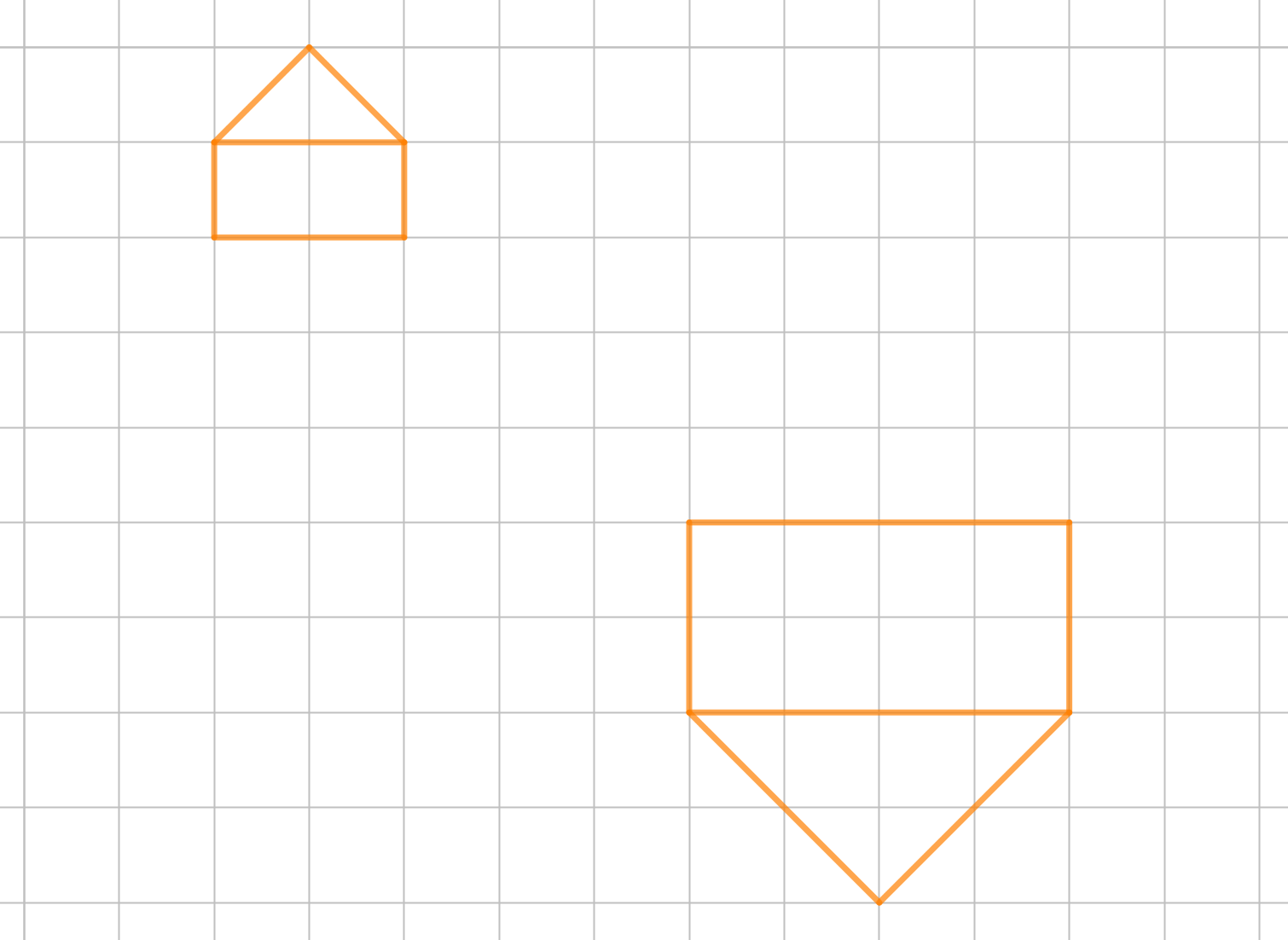
Promotrite likove na slici. Odredite središte i koeficijent homotetije kojom se manji lik preslikava u veći. Postavite središte homotetije na sliku.
Neka su zadane tri dužine i njihove duljine Četvrta geometrijska proporcionala jest dužina duljine Promotrite konstrukciju četvrte geometrijske proporcionale.
Opravdajte ispravnost konstrukcije četvrte geometrijske proporcionale.
Prisjetite se Eulerova pravca pa označite točne odgovore.
Eulerovu pravcu uvijek pripadaju
Eulerov pravac nije jedina zanimljiva veza između točaka trokuta. Istražit ćete još jednu zanimljivu vezu.
U interaktivnom predlošku nacrtan je raznostranični trokut
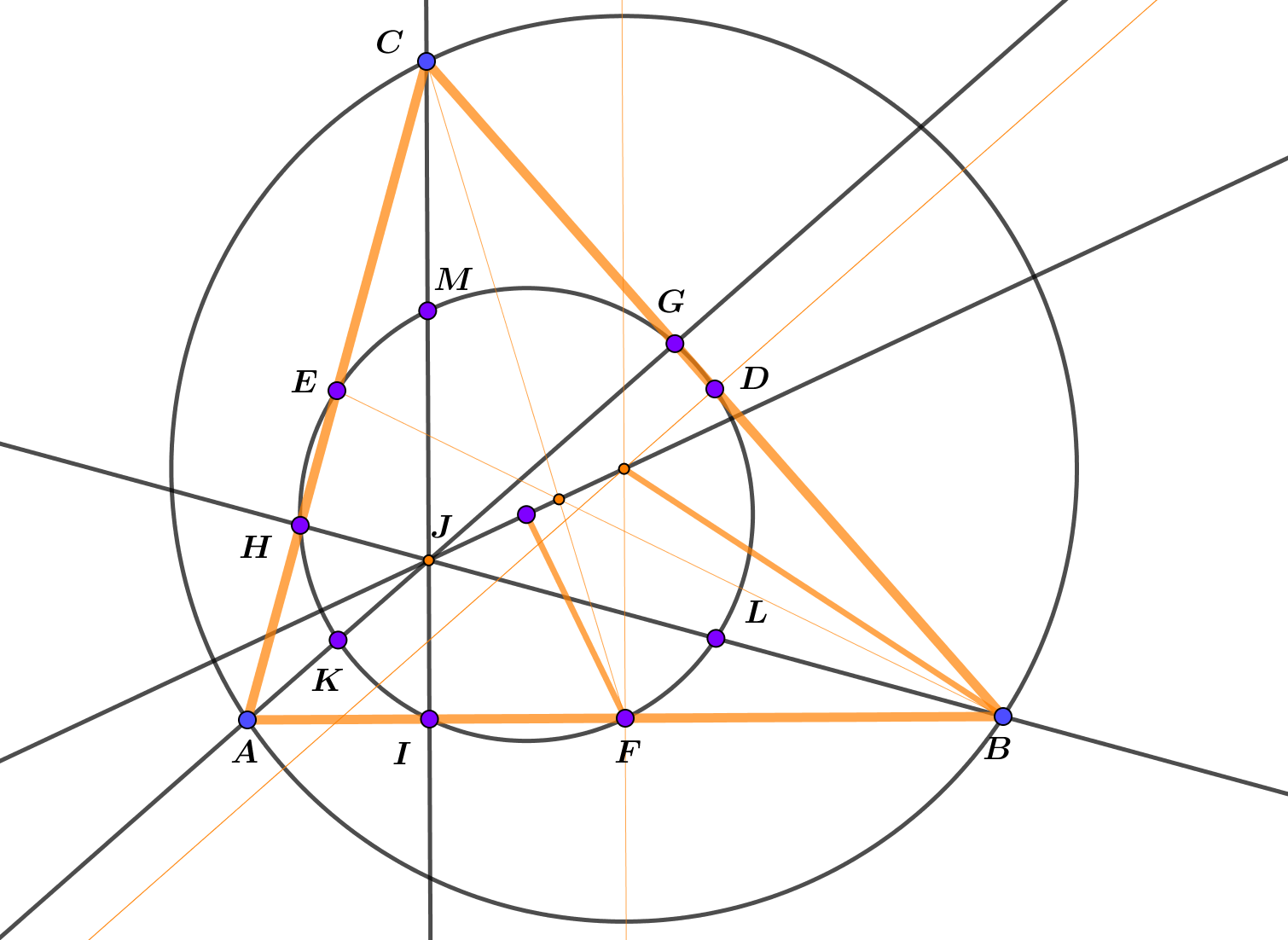
Devet točaka leži na istoj kružnici. Ta se kružnica zove Feuerbachova kružnica devet točaka. Njezino središte leži na Eulerovu pravcu, a polumjer joj je dvostruko manji od polumjera trokutu opisane kružnice.

Kružnica devet točaka ili Feuerbachova kružnica sadrži: polovišta stranica trokuta, nožišta visina i polovišta dužina koje spajaju vrh trokuta s ortocentrom. Ovu su vezu 1802. godine otkrili francuski matematičari Brianchon i Poncelet, a dokazao ju je godinu dana poslije njemački matematičar Karl Wilhelm Feuerbach.
U interakciji smo se uvjerili da bez obzira na to kako mijenjamo položaj vrhova trokuta, devet istaknutih točaka pripada istoj kružnici. Naravno, to nije matematički dokaz, nego provjeravanje velikog broja konkretnih primjera. Kako dokazati da za proizvoljni trokut
polovišta stranica trokuta,
nožišta visina i
polovišta dužina koje spajaju vrh trokuta s ortocentrom pripadaju istoj kružnici? Dokaz se provodi u nekoliko koraka. Možete ga pročitati na linku http://mnm.hr/wp-content/uploads/2016/10/Feuerbachova_kruznica.pdf
.

Mještani triju naselja dogovaraju se o izgradnji zajedničkih sportskih terena. Žele izgraditi terene na prostoru između svojih naselja. Naselja su udaljena
i
a već su izgrađene ravne ceste koje spajaju naselja. Dio projekta izgradnje terena jest i izgradnja prilaznih cesta kako bi sva tri naselja bila povezana s terenima. Predložite moguće položaje za izgradnju terena kao i prilaznih cesta uzimajući u obzir različite kriterije: udaljenost terena do pojedinih naselja, duljine prilaznih cesta, ukupne duljine puta do terena. Predočite prednosti pojedinih položaja, odredite duljine prilaznih cesta, obrazložite jesu li prijedlozi pravedni, je li neki prijedlog povoljniji za neka naselja.