


Zbog jakog vjetra, morskih struja, a najviše zbog ljudskog neiskustva i neopreznosti, ljeti se često događaju nesreće na moru. Organiziraju se traganja i spašavanja brodova i ljudi, a najčešće „hrabrih
” turista.
Lučka kapetanija Split zaprimila je dojavu o nestanku stranog turista u Bračkom kanalu. Krenuli su u potragu trima brodovima, od kojih je jedan bio u Milni, na otoku Braču, jedan u Rogaču, na otoku Šolti, a treći je krenuo iz Splita. Pred njima je težak zadatak. Krenimo u potragu!
Jedinična dužina na karti predstavlja u stvarnosti. Ishodište koordinatnog sustava je Split. Brodove ćemo nazvati prema mjestima iz kojih su krenuli u potragu i označiti s
Odredite kooordinate početnih pozicija brodova.
|
brod Split
|
|
|
brod Milna
|
|
|
brod Rogač
|
Brod Split plovio je
prema zapadu i
prema jugu. Brod Rogač plovio je
ravno prema istoku, a brod Milna plovio je
prema zapadu i
prema sjeveru. Odredite njihove nove pozicije u odnosu prema Splitu.
|
brod Rogač
|
|
|
brod Milna
|
|
|
brod Split
|
Prema signalima i dojavama ribara područje koje trebaju pretražiti proteže se od Duća, preko Splita, Drvenika, Rogača, Milne, pozicije O koja je zapadno i sjeverno od Milne, Postira i nazad do Duća. Ako svaki od brodova može iscrpno pretražiti kvadratna kilometra na sat, mogu li pretražiti cijelo područje u sata?
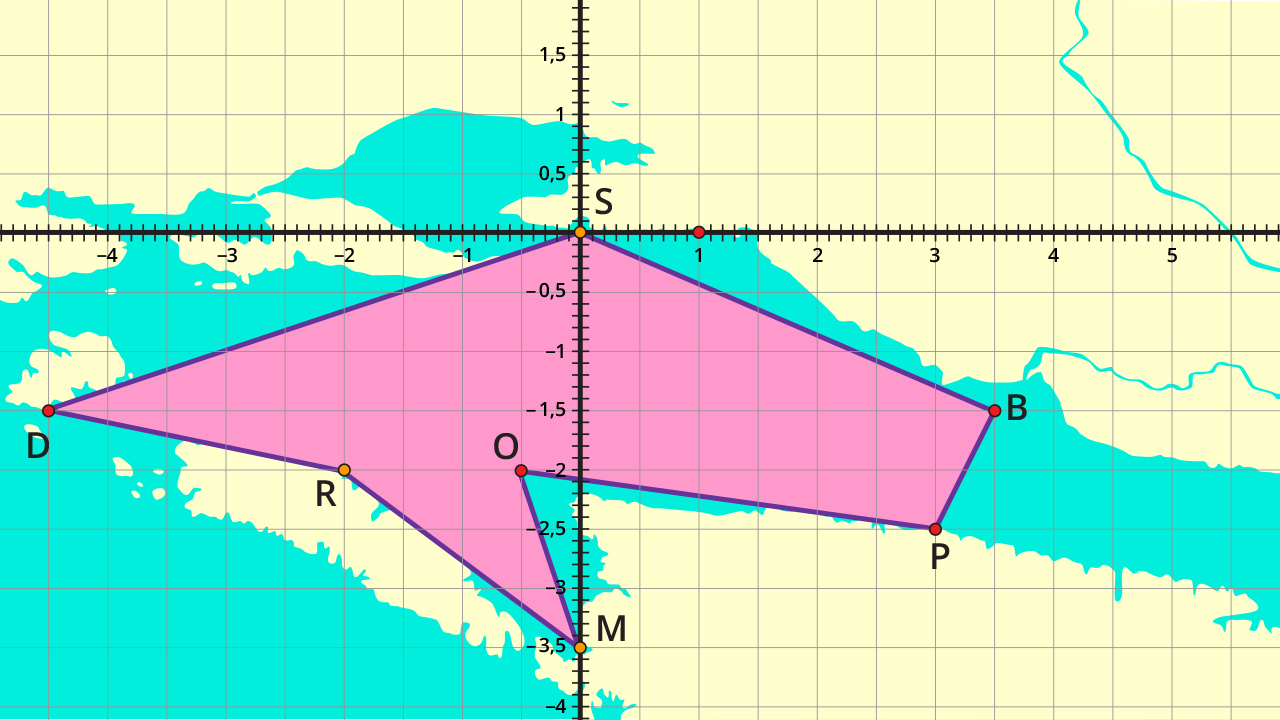
Postupak:
Površina područja pretrage iznosi približno kvadratne jedinice, što je približno
Brodovi mogu pretražiti dano područje jer za
sata mogu ukupno pretražiti
.
Koji je brod sada najbliži toj poziciji?
Pomoć:
Udaljenost je između broda Rogač i turista približno
(
jediničnih dužina).
Sve točke na osi
imaju koordinatu:
Označite sve uređene parove koji predstavljaju koordinate točaka jednako udaljenih od koordinatnih osi.
Točke simetrične su s obzirom na os Označite točne tvrdnje.
Točke
simetrične su s obzirom na ishodište.
Označite točne tvrdnje.
Ako su točke
kolinearne, označite točne tvrdnje.
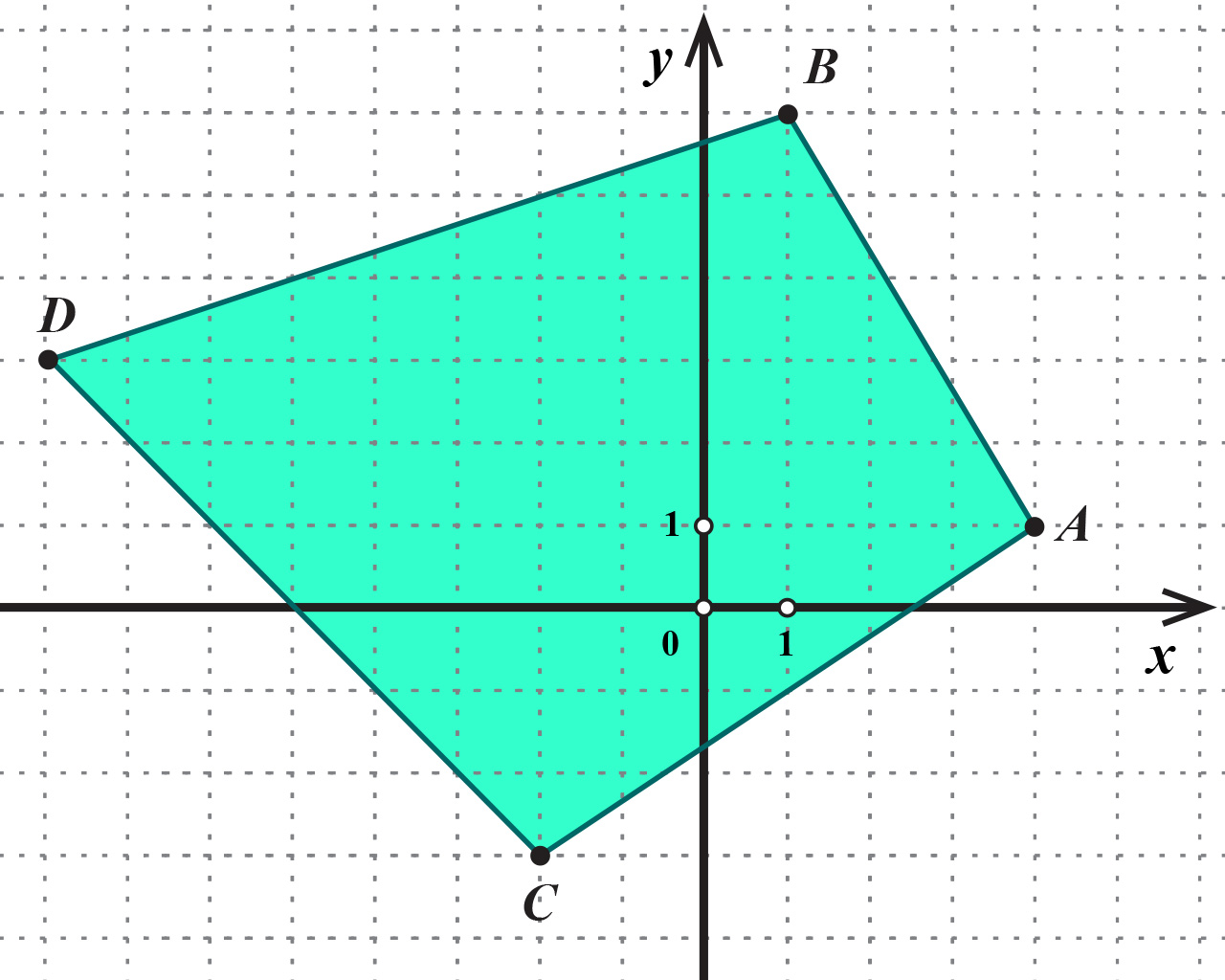
Izračunajte površinu četverokuta sa slike.
Površina je
kvadratnih jedinica.
Točke
su dva susjedna vrha paralelograma
a točka
je sjecište njegovih dijagonala.
Polovišta stranica
trokuta
su redom točke
Izračunajte površinu trokuta
Površina trokuta
je
kvadratnih jedinica.
Analitičku geometriju i koordinatnu metodu možemo, kao što ste vidjeli, primjenjivati za dokazivanje matematičkih tvrdnji i rješavanje zadataka.
No katkad, iako nam izgleda kao „sigurna ” metoda koja nas vodi rješenju, koordinatna metoda može biti znatno složenija i napornija za provođenje u usporedbi s nekom drugom metodom.
Uvjerite se u to u zadatku koji slijedi.
Ako su točke redom polovišta stranica trokuta istražite i objasnite u kakvu su odnosu:
Riješite prvo zadatak koristeći se koordinatama točaka
i rješenjem iz prethodnog zadatka, a zatim i općenito, za proizvoljni trokut.
Dužine srednjice su trokuta pa su njihove duljine jednake redom polovini duljina stranica
Površine su trokuta jednake.
Ako ste primjenjivali koordinatnu metodu za rješavanje zadatka s konkretnim brojevima, jednostavno ste dobili rješenje. U općem je slučaju puno raspisivanja i računanja s algebarskim izrazima pa je praktičnije primjenjivati neke činjenice i geometrijska svojstva u dokazu. Ako ste ih zaboravili, ponovit ćemo ih i proširiti u modulima koji slijede.

Ako u koordinatnom sustavu nacrtamo sve točke čije su koordinate cijeli brojevi, dobit ćemo kvadratnu mrežu, a nacrtane točke nazivamo čvorovi mreže.
Spajamo li redom niz točaka tako da se dobivene linije ne presijecaju i vratimo se u početnu točku, dobit ćemo jednostavan poligon kojemu se u svakom vrhu ili čvoru sastaju samo dvije linije. Spojnice dvaju vrhova ili čvorova još nazivamo bridovi poligona.
Neki će čvorovi mreže pritom biti na nacrtanoj liniji koju ćemo nazvati rub poligona, neki unutar poligona, a neki izvan poligona. Čvorove na rubu (i izvan) ispunit ćemo bojom („pune” točke), a u unutrašnjosti bijelom bojom („prazne” točke).
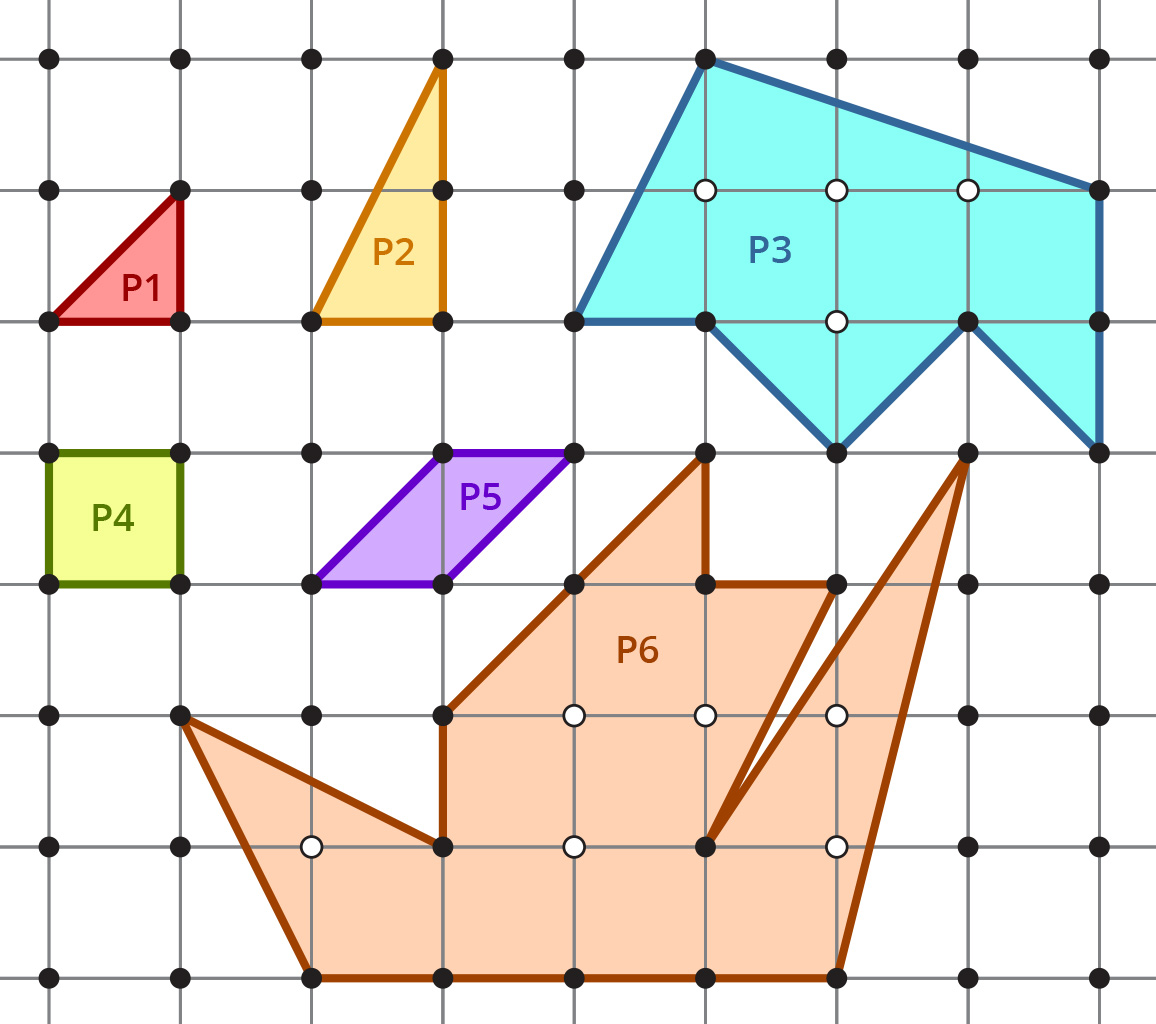
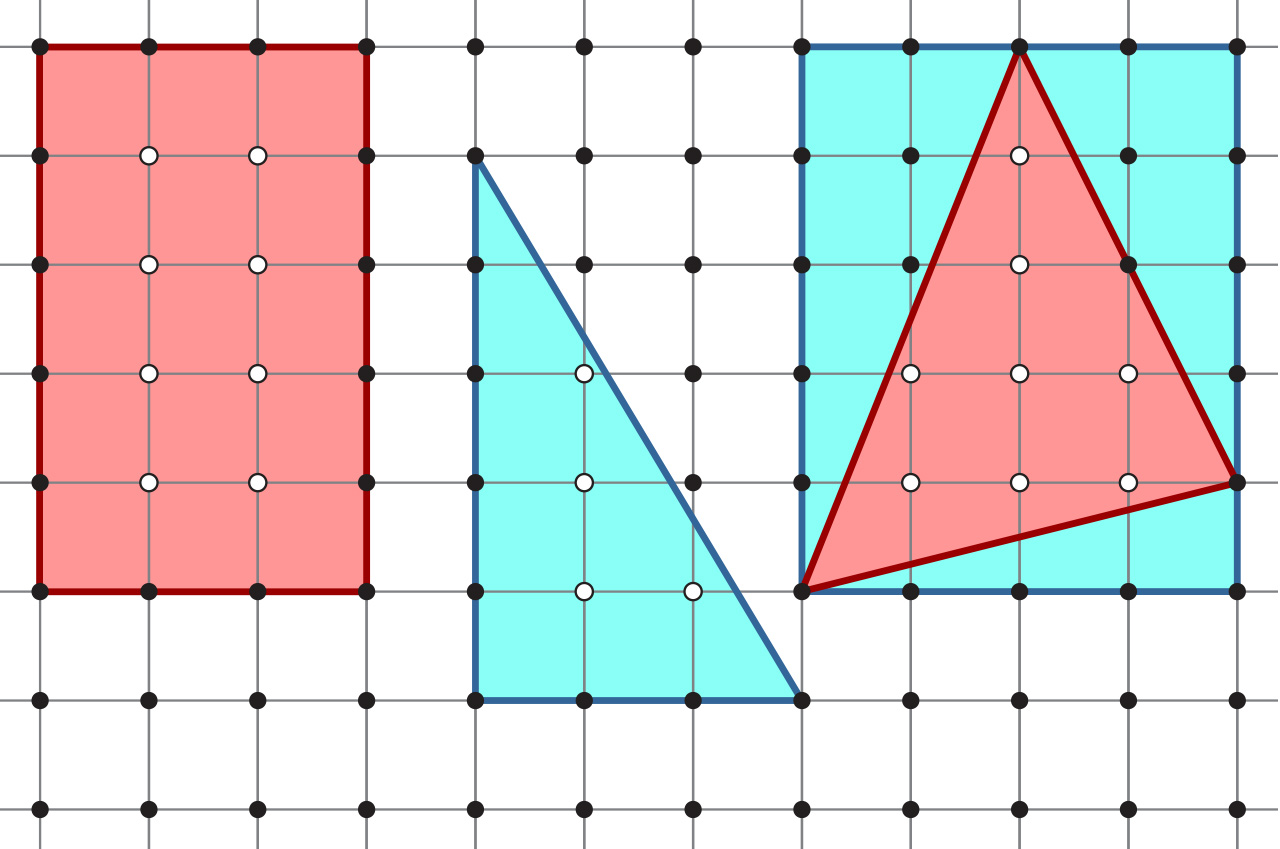
Na slici je prikaz nekoliko poligona u kvadratnoj mreži.
Broj ćemo rubnih čvorova označivati s a broj unutarnjih s
Tada je:
Postoji li neka veza među dobivenim brojevima Nacrtajte još poligona u kvadratnoj mreži i za svaki od njih odredite ta tri broja. Sve podatke zapišite pregledno u tablicu i pokušajte uočiti pravilnost. Počnite od jednostavnijih poligona prema složenijima.
Sljedeća će vam GeoGebrina interakcija u tome pomoći.
Odaberite znak računske radnje tako da dobijete točnu tvrdnju. Za dijeljenje upotrijebite znak /, a za množenje ×.
2
1.
Pickova formula:
Ako svi vrhovi jednostavnoga povezanog poligona imaju cjelobrojne koordinate, tada vrijedi:
gdje je broj vrhova na rubu poligona, broj vrhova unutar poligona, a površina poligona.
Ta se formula naziva Pickova formula.

Georg Alexander Pick (10. kolovoza 1859. – 26. srpnja 1942.) austrijski je matematičar. Poznat je po svojoj jednostavnoj formuli koju je otkrio još davne 1899. godine, ali objavio tek 1969. u knjizi Mathematical Snapshots by Steinhaus.
Manje je poznata, ali zanimljiva činjenica da je Georg Pick imao važnu ulogu u karijeri čuvenog fizičara Alberta Einsteina. Naime, jedan je od najzaslužnijih za njegovo imenovanje na njemačkom sveučilištu u Pragu 1911. godine. Tijekom dvije godine zajedničkog rada bili su nerazdvojni prijatelji, a osim znanosti povezivala ih je i glazba. Pick, koji je svirao u kvartetu, uveo je Einsteina u znanstvene i glazbene praške krugove. Govorilo se da je Pick imao veliku ulogu u razvoju Einsteinove opće teorije relativnosti te da je Pick upoznao Einsteina s dostignućima diferencijalne geometrije toga vremena. Einstein je dobio mjesto na Sveučilištu Princeton u SAD-u, a Georg Pick poslan je u nacistički logor Theresienstadt, u kojemu je umro 1942. godine.
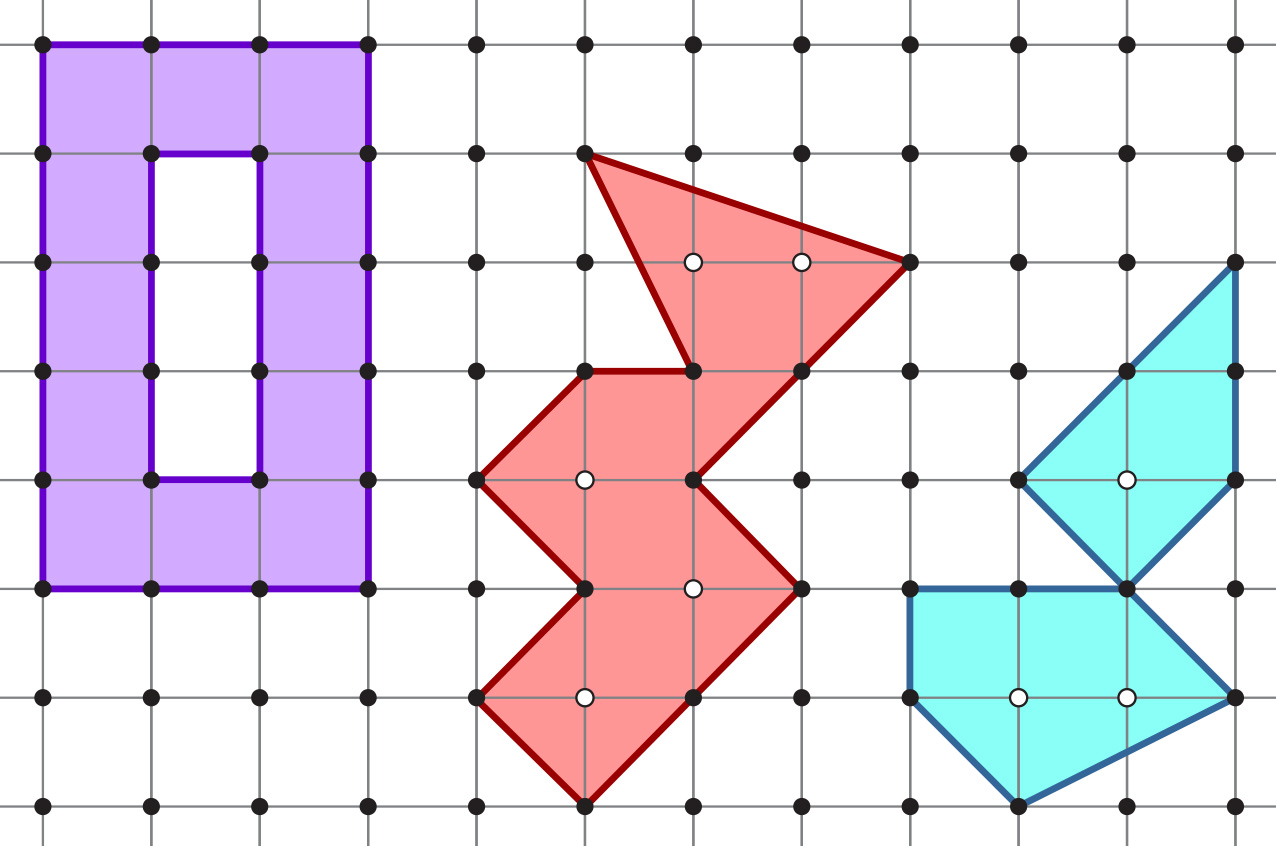
Provjerite vrijedi li Pickova formula za prikazane poligone.
Pickova formula ne vrijedi za posljednji, plavi poligon jer postoji vrh iz kojeg izlazi više od dvaju bridova, odnosno nije jednostavan poligon.
Pickova formula ne vrijedi ni za prvi, ljubičasti poligon jer ima „rupu ” , nije povezan poligon.
Pickova formula vrijedi za srednji, crveni poligon.

U novome hotelskom naselju gradi se veliki park površine i treba postaviti prskalice za vodu kako bi se trava lakše zalijevala i imala lijepu zelenu boju.
Tijekom projektiranja u vrtu su kolcima i špagom napravili kvadratnu mrežu. Posebnom su špagom oko kolaca označili rub područja unutar kojeg će postaviti prskalice. To područje obuhvaća površine cijelog parka, a prskalice će postaviti u čvorove mreže. Kolci su međusobno razmaknuti metra (horizontalno i vertikalno). Koliko prskalica treba postaviti unutar označenog područja?
Pickova je formula vrlo jednostavna formula s kojom ste se možda susreli i u ranijoj dobi. Primjerice, dok ste učili i istraživali na geoploči.
Matematičari vole jednostavne stvari, ali isto tako vole za sve što naslute ili upotrebljavaju znati jasan razlog zašto je to tako. Jeste li se pitali zašto vrijedi Pickova formula? Možemo li je objasniti jednostavnim matematičkim argumentima?
Njezin dokaz nije tako kratak i jednostavan kao sama formula, ali mnoge dijelove možete razumjeti i samostalno napraviti.
Istražite različite pristupe u dokazivanju – od geometrijskoga, algebarskoga do induktivnog pristupa – za one koji žele još malo više.
Možda će vam pritom pomoći sljedeći zadatak i GeoGebrin interaktivni zadatak koji ste upotrebljavali na početku istraživanja.
Neka su stranice pravokutnika
odnosno
jediničnih dužina kvadratne mreže.
Uočite da na svakoj stranici pravokutnika postoji jedan rubni čvor više nego što je njezina duljina. Ukupan broj rubnih čvorova jednak je zbroju čvorova na stranicama umanjenom za
jer smo svaki vrh pravokutnika brojili dva puta (jer se nalazi na dvjema stranicama). Zato je ukupan broj rubnih čvorova jednak opsegu, odnosno
Isto tako
Tada je
Dokaz se svodi na prethodni slučaj, odnosno pravokutnik ako pokažete da broj čvorova na hipotenuzi možemo zanemariti! Zašto?
(Uputa: Pretpostavite da postoji čvorova na hipotenuzi.)
Proizvoljan se trokut može u kvadratnoj mreži promatrati kao dio pravokutnika kojem se oduzme nekoliko pravokutnih trokuta. Tako se taj slučaj svodi na prethodne uz malo računanja s algebarskim izrazima. Provedite računanje.
Zabavimo se...
U kvadratnoj mreži ucrtano je točaka koje su vrhovi kvadrata. Šest je točaka označeno crvenom bojom. To su vrhovi koji su zajednički za dva kvadrata.
Pronađite svih devet kvadrata.
Odaberite u svakom kvadrantu po tri ili četiri nekolinearna vrha kvadrata tako da svi odabrani vrhovi spojeni linijom tvore jednostavan i povezan poligon. Ispišite koordinate njegovih vrhova i izračunajte površinu dobivenog poligona.