1.5 Apsolutna vrijednost realnog broja

Kolika je razlika?

U stvarnome životu vrlo često računamo razliku između dviju veličina. Obično govorimo:

• „Razlika u jutarnjoj i podnevnoj temperaturi zraka je $\mathrm{10\; ℃}.$"

• „Savladali su razliku nadmorske visine od $120$ metara."
  

• „Izgubili smo utakmicu za $1$ koš."
  

• „Moja se računica razlikuje od tvoje u $15$ kuna."
  

Uočimo da je razlika koju smo izračunali nekad pozitivna, a nekad negativna. No u većini je slučajeva prirodnije dobiveni iznos izreći kao pozitivan broj, a predznak razlike izreći u kontekstu ( $3\mathrm{cm}$ previše), a ne eksplicitno ga navesti $\left(-3\mathrm{cm}\right).$ Zašto nam je to prirodnije?

Udaljenost

Za pozitivan broj koji smo upotrijebili u navedenim iskazima kažemo da je apsolutna vrijednost dobivene razlike. ​

Za brojeve $-3$ ili $3$ apsolutna je vrijednost broj $3.$ To zapisujemo $\left|-3\right|=3$ i $\left|3\right|=3.$

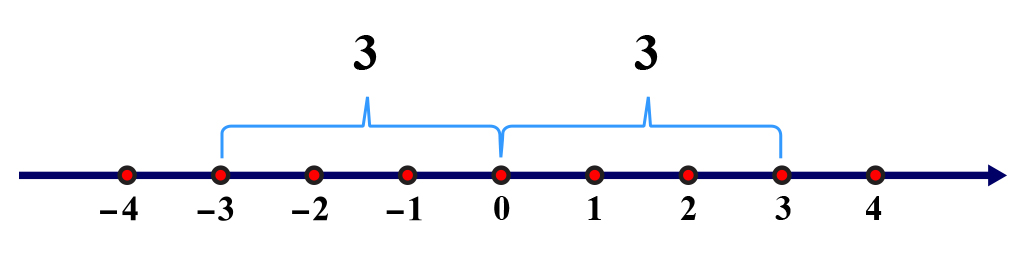
Koliko su brojevi $3$ i $-3$ udaljeni od nule na brojevnom pravcu?

Brojevi $-3$ i $3$ su od broja $0$ udaljeni za tri jedinice na brojevnom pravcu.

Apsolutna vrijednost realnog broja $x$ mjeri njegovu udaljenost od nule na brojevnom pravcu i označavamo je s $\left|x\right|$ $.$

Kolekcija zadataka 1

Zadatak 1.

Ako je $x$ pozitivan realni broj, što je njegova apsolutna vrijednost $\left|x\right|?$ ​

Uparite pozitivne realne brojeve s njihovom apsolutnim vrijednostima.

$\sqrt{3}-1$  ​	$\frac{2}{5}$  ​
$\frac{2}{5}$  ​	$\sqrt{3}$ ​
$3.5$	$\sqrt{3}-1$  ​
$\sqrt{3}$  ​	$a$
$a$  ​	$20$
$20$	$3.5$

null

null

Zadatak 2.

Ako je $x$ negativan realni broj, što je njegova apsolutna vrijednost $\left|x\right|$? ​

Svakome negativnome realnom broju pridružite izraz koji određuje njegovu apsolutnu vrijednost.

$-\frac{2}{5}$  ​	$-(-3.5)=3.5$
$-\sqrt{3}$	$-(1-\sqrt{3})=\sqrt{3}-1$
$-3.5$	$-(-\sqrt{3})=\sqrt{3}$
$-20$	$-(-\frac{2}{5})=\frac{2}{5}$
$1-\sqrt{3}$  ​	$-\left(-20\right)=20$
$-a,a>0$  ​	$-(-a)=a$  ​

null

null

Zadatak 3.

Promotrite dobivene rezultate iz prethodne tablice. Otkrijte koja je od sljedećih tvrdnji netočna.

1. Apsolutna je vrijednost pozitivnoga realnog broja $x$ uvijek pozitivan broj.
   

   Da

   Ne

   

   null

   null

2. Broj $x$ i $-x$ uvijek imaju istu apsolutnu vrijednost.
   

   Da

   Ne

   

   null

   null

3. Pozitivan je realni broj $x$ od nule udaljen za $x$ jedinica na brojevnom pravcu.
   

   Da

   Ne

   

   null

   null

4. Negativan je realni broj $x$ od nule udaljen za $x$ jedinica na brojevnom pravcu.
   

   Da

   Ne

   

   null

   null

5. Negativan je realni broj $x$ od nule udaljen za $-x$ jedinica na brojevnom pravcu.
   

   Da

   Ne

   

   null

   null

6. Apsolutna je vrijednost pozitivnoga realnog broja $x$ taj isti realni broj $x.$
   

   Da

   Ne

   

   null

   null

7. Apsolutna je vrijednost negativnoga realnog broja $x$ jednaka njegovu suprotnom broju.
   

   Da

   Ne

   

   null

   null

Zatvori

Zašto minus ?

Za negativne realne brojeve $\left|x\right|=-x.$ Zašto znak za minus ako je apsolutna vrijednost uvijek pozitivan broj?

Primjer 1.

Kako se definicijom apsolutne vrijednosti koristimo pri računanju?

$\left|54\right|=54$ jer je broj $54$ pozitivan. Broj $54$ od $0$ je udaljen za $54$ jedinice na brojevnom pravcu.

$\left|0\right|\text{=0,}$ jer je broj $0$ udaljen od $0$ za $0$ jedinica na brojevnom pravcu.

$\left|-32\right|=-\left(-32\right)\text{,}$ jer je broj $-32$ negativan te je njegova apsolutna vrijednost njemu suprotan broj. Od $0$ je udaljen za $32$ jedinice na brojevnom pravcu.

$|-\sqrt{2}|=-(-\sqrt{2})=\sqrt{2},$ jer je broj pozitivan i od $0$ je udaljen za $\sqrt{2}$ jedinice na brojevnom pravcu.

Zadatak 4.

Ako znamo apsolutnu vrijednost realnog broja $x,$ možemo li odrediti broj $x?$

Je li taj broj jedinstven?

Objasnite sljedeće svojstvo.  ​

Neka je $a\ge 0.$ Tada iz $\left|x\right|=a$ slijedi $x=a\mathrm{ili}x=-a.$

Kolekcija zadataka 2

Zadatak 5.

Dovucite zadane elemente na pravo mjesto.

U jednu grupu dovucite brojeve koji mogu biti apsolutna vrijednost nekoga broja, a u drugu grupu one koji to ne mogu biti:

$1-\sqrt{2}$

$1+\sqrt{2}$

$\frac{-2}{-13.1}$

$12.6$

$-120$

$-\sqrt{10}$

$\pi -1$

$100$

$0.000012$

$\frac{11}{13}$

$-\left(\frac{-24}{-3}\right)$

$-\frac{1}{0.012}$

$1.002-1.006$

$3·\left(\begin{array}{l}2.3-3.2\end{array}\right)$

$0$​

$-0.23002$

 Apsolutna vrijednost

Nije apsolutna vrijednost

null

null

Zadatak 6.

Zadan je niz apsolutnih vrijednosti. Poredajte ih po veličini od najmanje do najveće.

Poredajte brojeve povlačenjem tako da su u traženom poretku.

• $\left|-21\right|$
• $\left|\begin{array}{l}22\end{array}\right|$
• $\left|-14.2\right|$
• $\left|-43\right|$
• $\left|\begin{array}{l}14.3\end{array}\right|$ ​
• $\left|-42\right|$
• $\left|\begin{array}{l}44\end{array}\right|$
• $\left|\begin{array}{l}-51\end{array}\right|$
• $\left|-14.6\right|$
• $\left|\begin{array}{l}67\end{array}\right|$ ​

null

null

Zatvori

Apsolutna vrijednost i udaljenost na brojevnom pravcu

Kolekcija zadataka 3

Zadatak 7.

Brojevi $a$ i $b$ pridruženi su redom točkama $A$ i $B$ na brojevnom pravcu. Mijenjajte položaj točaka $A$ i $B.$ Pritom promatrajte njihovu međusobnu udaljenost $d(A,B)$ i apsolutnu vrijednost $|a-b|.$

Što zamjećujete?

Što u geometrijskom smislu predstavlja izraz $|a-b|?$

Umetnite odgovarajuću riječ tako da dobijete istinitu tvrdnju.

Apsolutna vrijednost $\left|\begin{array}{l}a-b\end{array}\right|$  predstavlja između brojeva $a$ i $b$ na brojevnom pravcu.

null

null

Zadatak 8.

Svaki od izraza s apsolutnom vrijednošću uparite s njegovim geometrijskim značenjem.

$\left|a+5\right|\ge 3$	broj $\mathrm{<mi>\; a\; </mi>}$ je od $-5$ udaljen za više ili jednako $3$
$\left|a-1.5\right|=2$	broj $\mathrm{<mi>\; a\; </mi>}$ je od $5$ udaljen za manje od $3$
$\left|5.8-a\right|$	broj $\mathrm{<mi>\; a\; </mi>}$ je od $1.5$ udaljen za $2$
$\left|a\right|=2$	broj $a$ je udaljen od $0$ za $2$
$\left|a-3\right|$	udaljenost realnog broja $a$ od $3$
$\left|a-5\right|<3$	udaljenost realnog broja $a$ od $5.8$
$\left|a+3\right|$	udaljenost realnog broja $a$ od $-3$

null

null

Zatvori

Svojstva apsolutne vrijednosti

Kolekcija zadataka 4

Zadatak 9.

Za realne brojeve​ $a$ i $b$ izračunajte apsolutne vrijednosti i usporedite dobivene rezultate (zaokružene na dvije decimale).

Što možete zaključiti o brojevima $\left|\begin{array}{l}a·b\end{array}\right|$ i $\left|\begin{array}{l}a\end{array}\right|·\left|\begin{array}{l}b\end{array}\right|,$ a što o brojevima $\left|\frac{a}{b}\right|$ i $\frac{\left|a\right|}{\left|b\right|}$ na osnovi provedenog istraživanja?

Rješenje

$\left|\begin{array}{l}a·b\end{array}\right|$ = $\left|\begin{array}{l}a\end{array}\right|·\left|\begin{array}{l}b\end{array}\right|$

$\left|\frac{a}{b}\right|=\frac{\left|a\right|}{\left|b\right|}$

---

Zadatak 10.

Za realne brojeve​ $a$ i $b$ izračunajte apsolutne vrijednosti i usporedite dobivene rezultate.   

Zatvori

Kolekcija zadataka 5

Zadatak 11.

Na osnovi provedenog istraživanja riješite zadatak.

Uparite tvrdnje tako da dobijete svojstva apsolutne vrijednosti realnoga broja.

$\left|\begin{array}{l}a+b\end{array}\right|$	$\le \left|\begin{array}{l}a\end{array}\right|+\left|\begin{array}{l}b\end{array}\right|$
$|-b|$	$=\left|\begin{array}{l}b-a\end{array}\right|$
$\left|\begin{array}{l}a·b\end{array}\right|$	$\ge 0$
$\left|a\right|$	$=\left|\begin{array}{l}a\end{array}\right|·\left|\begin{array}{l}b\end{array}\right|$
$\left|a\right|-\left|b\right|$	$\le \left|\begin{array}{l}a-b\end{array}\right|$
$\left|\begin{array}{l}\frac{a}{b}\end{array}\right|$	$=\left|b\right|$
$\left|\begin{array}{l}a-b\end{array}\right|$	$=\frac{\left|a\right|}{\left|b\right|}$

null

null

Primijenite svojstva apsolutne vrijednosti pri računanju u sljedećim zadatcima.

Zadatak 12.

Ako je $a=-4$ $,$ $b=9,$ izračunajte:

1. $|3a+b|$ 
2. $a-|-2b|$ 
3. $\left|\frac{a}{2b}\right|$
4. $|a+b|-5$ 
5. $\left|\begin{array}{l}\frac{\left|\begin{array}{l}2a-b\end{array}\right|}{a}\end{array}\right|.$

Rješenje

1. $3$
2. $-22$
3. $\frac{2}{9}$
4. $0$
5. $\frac{17}{4}$

---

Zatvori

Račun pogreške

Svi ćemo se složiti da je u realnom svijetu teško provesti savršeno mjerenje i odrediti točnu ili stvarnu vrijednost veličine koju mjerimo. Je li beznačajna nastala pogreška? Kako ćemo izmjeriti veličinu i procijeniti kvalitetu pogreške?

Mjere za pogrešku

Neka je $x$ stvarna (točna) vrijednost, a $x_m$ izmjerena vrijednost ili aproksimacija stvarne vrijednosti. ​

Apsolutna pogreška je odstupanje izmjerene vrijednosti $x_m$ od stvarne vrijednosti $x.$ Računa se kao apsolutna vrijednost njihove razlike i označava se s $∆x.$ Pišemo:

$∆x=\left|{x-x}_m\right|.$

Relativna pogreška $\mathit{(}r\mathit{)}$ mjeri relativnu točnost izmjerene vrijednosti $x_m$ u odnosu prema stvarnoj vrijednosti $x.$ Računa se kao omjer apsolutne pogreške i stvarne vrijednosti, a obično se iskazuje u postotku. Pišemo:

$\mathit{\text{r}}\mathit{=}\frac{∆x}{x}\mathrm{=}\frac{\left|x-x_m\right|}{x}.$

Primjer 2.

Što je lošije – izmjeriti $1\mathrm{kg}$ umjesto $0.6\mathrm{kg}$ ili $151\mathrm{kg}$ umjesto $150.6\mathrm{kg}?$

Apsolutna je pogreška u obama slučajevima ista:

$\Delta x=\left|1-0.6\right|=\left|151-150.6\right|=0.4\mathrm{\text{kg}}$ 

Bez obzira na rezultat, osjećamo da to nije ista pogreška. Pogledajmo kako izgleda relativna pogreška. Relativna je pogreška u prvom slučaju:

$r=\frac{∆x}{x}=\frac{0.4}{0.6}=0.666\dots \approx 0.667.$

Relativna je pogreška u drugom slučaju:

$r=\frac{∆x}{x}=\frac{0.4}{150.6}=0.002656\approx \mathrm{0.003.}$

Ako to zapišemo kao postotak, dobivamo redom $66.7\%$ i $0.3\%.$ (Prisjetite se pojma postotka: Matematika 7, Modul 3)

Sada je potpuno jasno da je veća greška izmjeriti $1\mathrm{kg}$ umjesto $0.6\mathrm{kg}$ nego $151\mathrm{kg}$ umjesto $150.6\mathrm{kg}.$

Zadatak 13.

Broj $a\mathrm{=}\mathrm{12.345}$ zaokružite na jednu decimalu i odredite apsolutnu i relativnu pogrešku nastalu pri zaokruživanju.

Uočite:

Ako je $∆x=\left|{x-x}_m\right|,$ tada je $x=x_m\pm ∆x.$

Zadatak 14.

Kako biste dokazali prethodnu tvrdnju?

Sljedeće elemente poredajte tako da dobijete sve korake u dokazu dane tvrdnje.

Izmjerena vrijednost $x_m$ može biti veća ili manja od stvarne vrijednosti $x.$ Tada je

• $x-x_m=\pm △x\Rightarrow$
• $x-x_m\ge 0\mathrm{ili}x-x_m\le 0\Rightarrow$
• $x=x_m\pm △\mathrm{x.}$

null

null

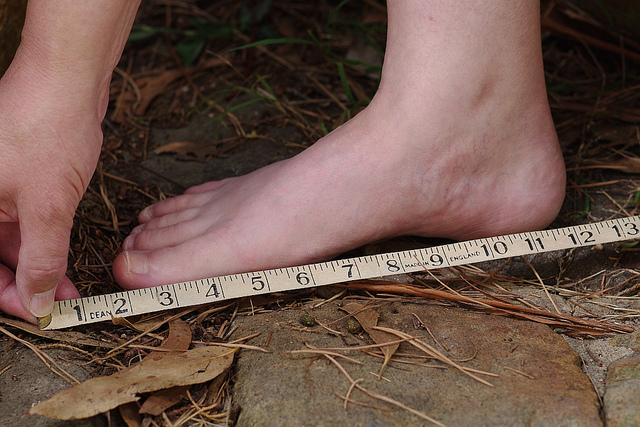
Primjer 3.

Mjereći duljinu svojeg stopala učenik je dobio broj koji se nalazi između dviju oznaka za $\mathrm{cm},$ a u bilježnicu zapisao kao rezultat $28\mathrm{cm}.$ Koliko će najviše njegovo mjerenje biti neprecizno? Smatramo da je mjerenje precizno do $\pm 0.5$ od najmanje podjele na nekoj ljestvici. Koju stvarnu duljinu može imati njegovo stopalo?

Izračunajmo apsolutnu i relativnu pogrešku njegova mjerenja.

Procjena je stvarne duljine učenikova stopala $(28\pm 0.5)\mathrm{cm}$ .

Apsolutna je pogreška $0.5\mathrm{cm},$ a relativna $\frac{∆x}{x}=\frac{0.5}{28}=0.017857\approx 1.8\%.$