

Ponovimo.
Linearna funkcija zadana je pravilom pridruživanja
Kolika je vrijednost funkcije za vrijednost argumenta
Kolika je vrijednost argumenta za vrijednost funkcije
Kako se promijeni vrijednost funkcije ako se vrijednost argumenta poveća za
Koliko je
Popunite sljedeću tablicu koja prikazuje vrijednosti funkcije zadane pravilom pridruživanja


Za linearnu funkciju prikazanu grafom u koordinatom sustavu izračunajte traženu vrijednost argumenta, odnosno vrijednost funkcije.
Kojoj se od navedenih linearnih funkcija vrijednost poveća za
kada se vrijednost argumenta smanji za
Kojoj se od navedenih linearnih funkcija vrijednost smanji za
kada se vrijednost argumenta smanji za
Kojoj se od navedenih linearnih funkcija vrijednost poveća za
kada se vrijednost argumenta poveća za
Kojoj se od navedenih linearnih funkcija vrijednost smanji za
kada se vrijednost argumenta poveća za
Za funkciju apsolutne vrijednosti zadanu pravilom pridruživanja upišite vrijednosti koje nedostaju.
Uparite pravilo pridruživanja i vrijednosti funkcije apsolutne vrijednosti.
|
|
|
|
|
|
|
|
|
|
|
|
Diskutirajte o broju rješenja jednadžbe u ovisnosti o realnom broju
Prvo ćemo nacrtati graf funkcije
Pogledajmo sljedeću animaciju. Pratite koliko zajedničkih točaka imaju dva nacrtana grafa.

Za projekt iz Biologije učenici su bilježili podatke o rastu crvenoga hrasta i tise posađenih u školskom dvorištu. Ustanovili su da crveni hrast raste
centimetara godišnje, a tisa naraste
centimetara za dvije godine. Podatke o visini stabala u ovisnosti o proteklom vremenu od početka promatranja prikazali su u sljedećem koordinatnom sustavu.
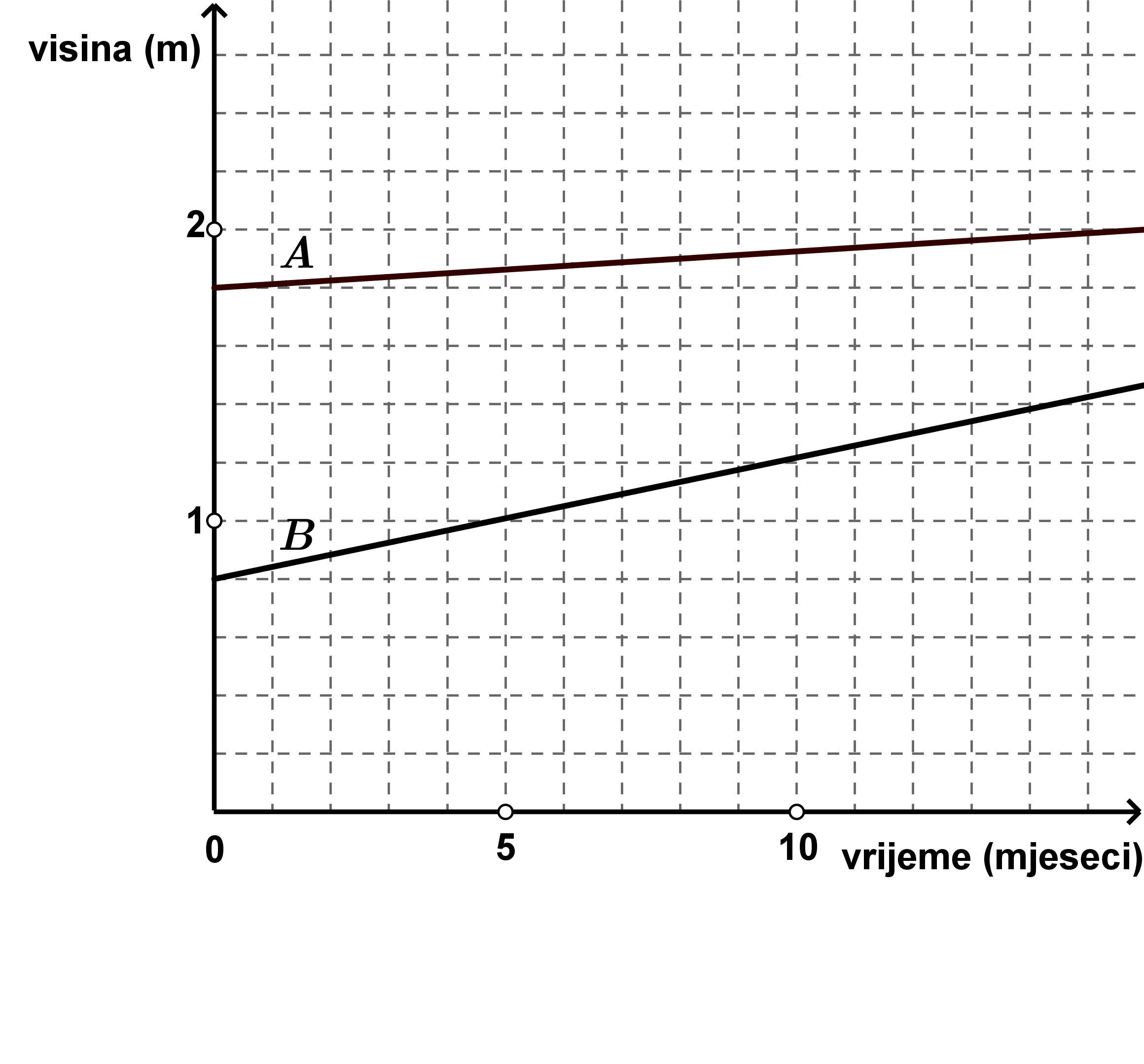
Nakon koliko će vremena tisa biti visoka
metra?
Koliko se svakoga mjeseca promijeni razlika visina tih dvaju stabala?
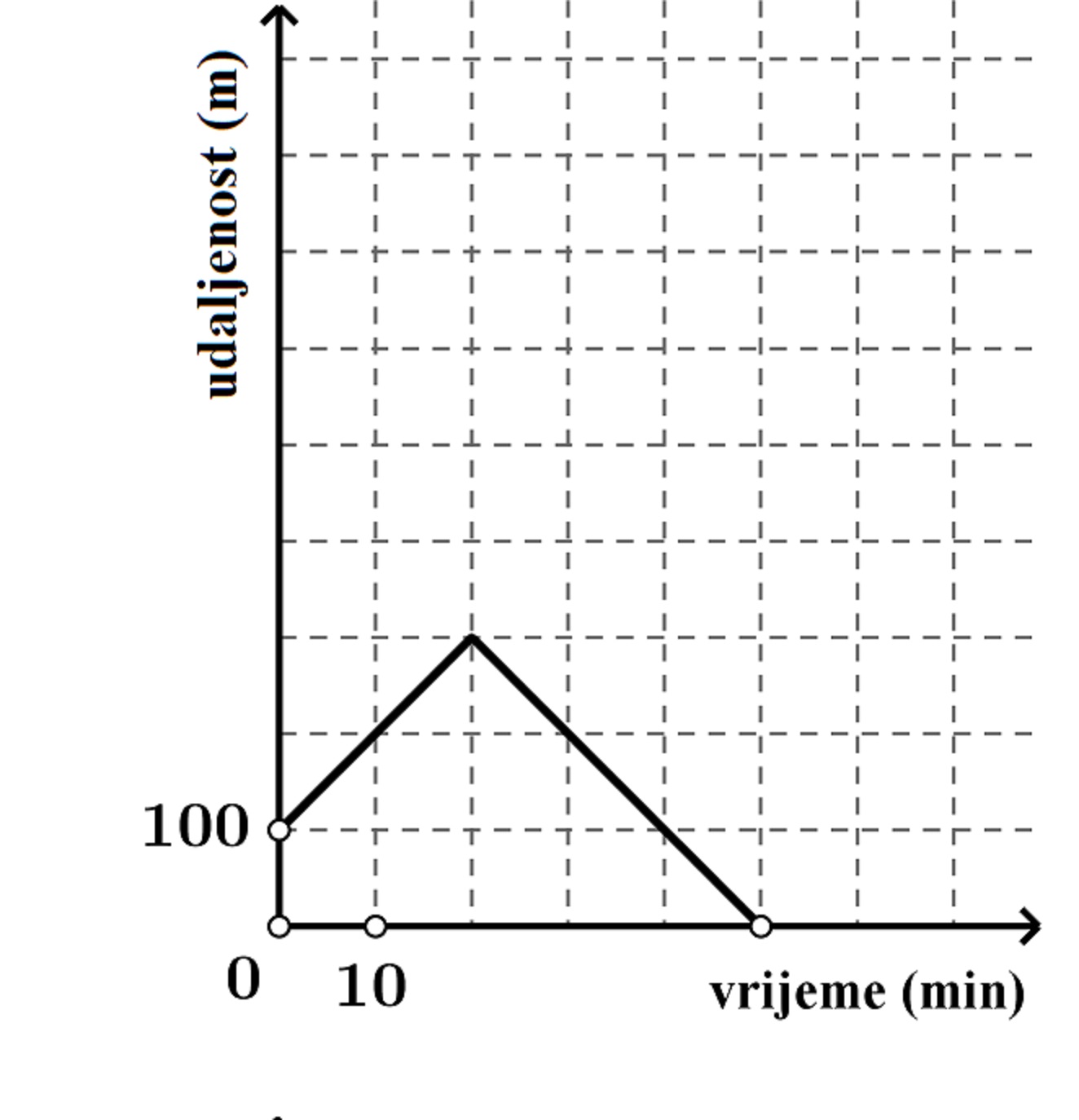
Nela je bila kod prijateljice Vedrane pa su se odlučile prošetati. Nakon nekog su se vremena okrenule i vratile Nelinoj kući.
U koordinatnom je sustavu prikazan graf funkcije koji opisuje kako udaljenost od Neline kuće izražena u metrima ovisi o proteklome vremenu izraženom u minutama.
Matej svaki dan pješači od kuće do škole koja je udaljena kilometar. U sljedećim je interakcijama grafom prikazano njegovo kretanje do škole u tri različita dana. Napišite priču o svakome danu. Provjerite.

Prebrojivi skupovi
Skup koji ima konačan broj elemenata nazivamo konačnim skupom.
Za skup kažemo da je beskonačan ako nije konačan. Beskonačan skup može biti prebrojiv ili neprebrojiv.
Beskonačan skup prebrojiv je ako se njegovi elementi mogu poredati u niz: Očito je skup prirodnih brojeva prebrojiv. Ekvivalentno tomu, skup je prebrojiv ako postoji bijekcija
Definiramo bijekciju

Do grada Motovuna vodi najduže istarsko stubište s više od tisuću stuba. Procjenjuje se da se petstota stuba nalazi otprilike na metara nadmorske visine. Pronađite potrebne podatke kako biste zapisali ovisnost nadmorske visine o rednom broju stube. Prikažite grafički dobivenu funkciju. Na koliko se metara nadmorske visine nalazi početak stubišta? Kolika je prosječna visina jedne stube?
Istražite još neke gradove u Istri do kojih vode dugačka stubišta i modelirajte ih linearnom funkcijom.