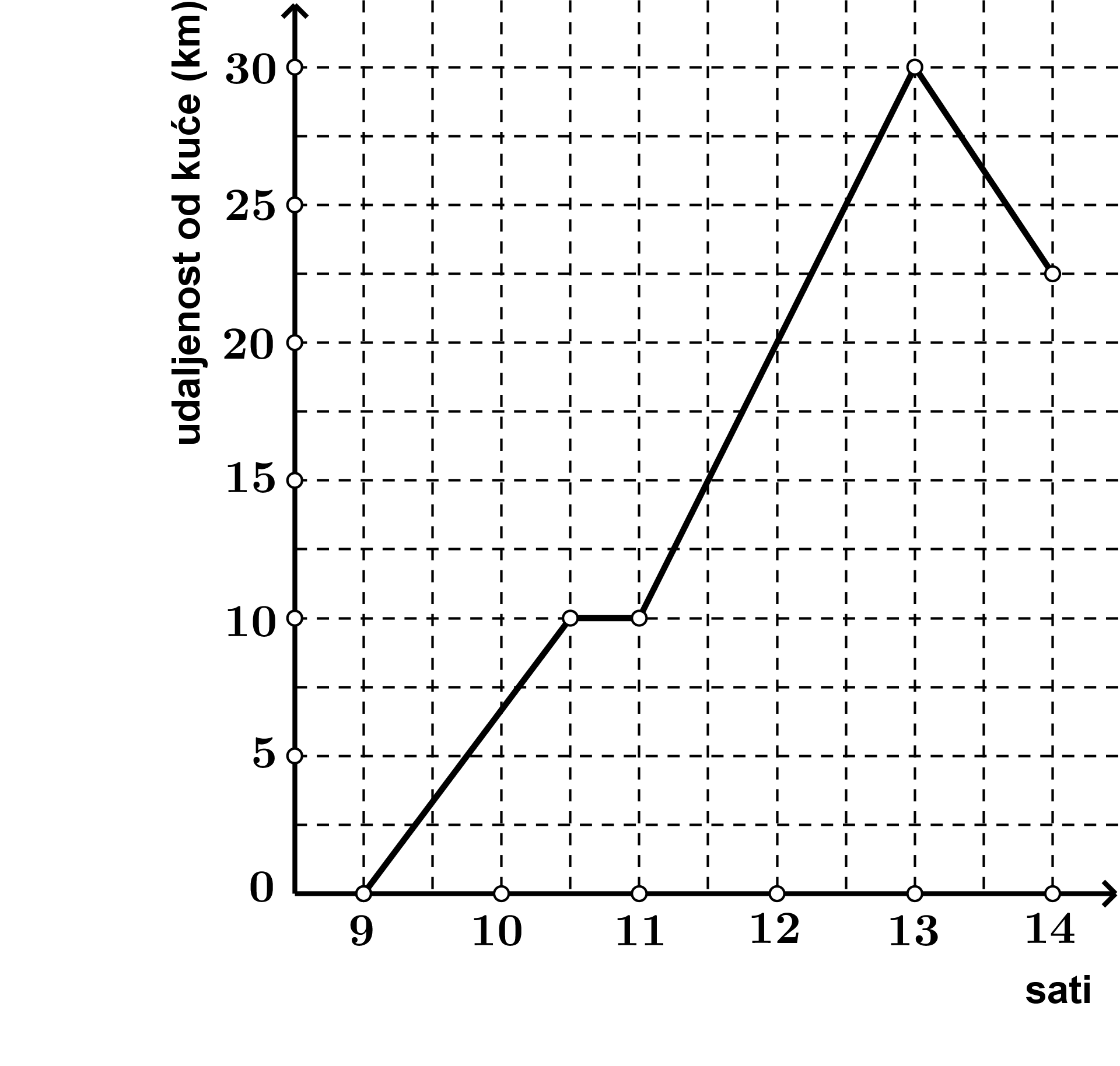
Uparite pravila pridruživanja i njihove domene i slike funkcije.
|
|
|
|
|
|
|
|
|
|
|
|
Linearna funkcija, zadana pravilom pridruživanja bit će rastuća za .
U koordinatnom je sustavu nacrtan graf linearne funkcije Smjestite ponuđene vrijednosti na odgovarajuća mjesta.

4
10
U koordinatnom je sustavu nacrtan graf linearne funkcije
Smjestite ponuđene vrijednosti na odgovarajuća mjesta.

2
0.3
U koordinatnom je sustavu nacrtan graf linearne funkcije
Smjestite ponuđene vrijednosti na odgovarajuća mjesta.
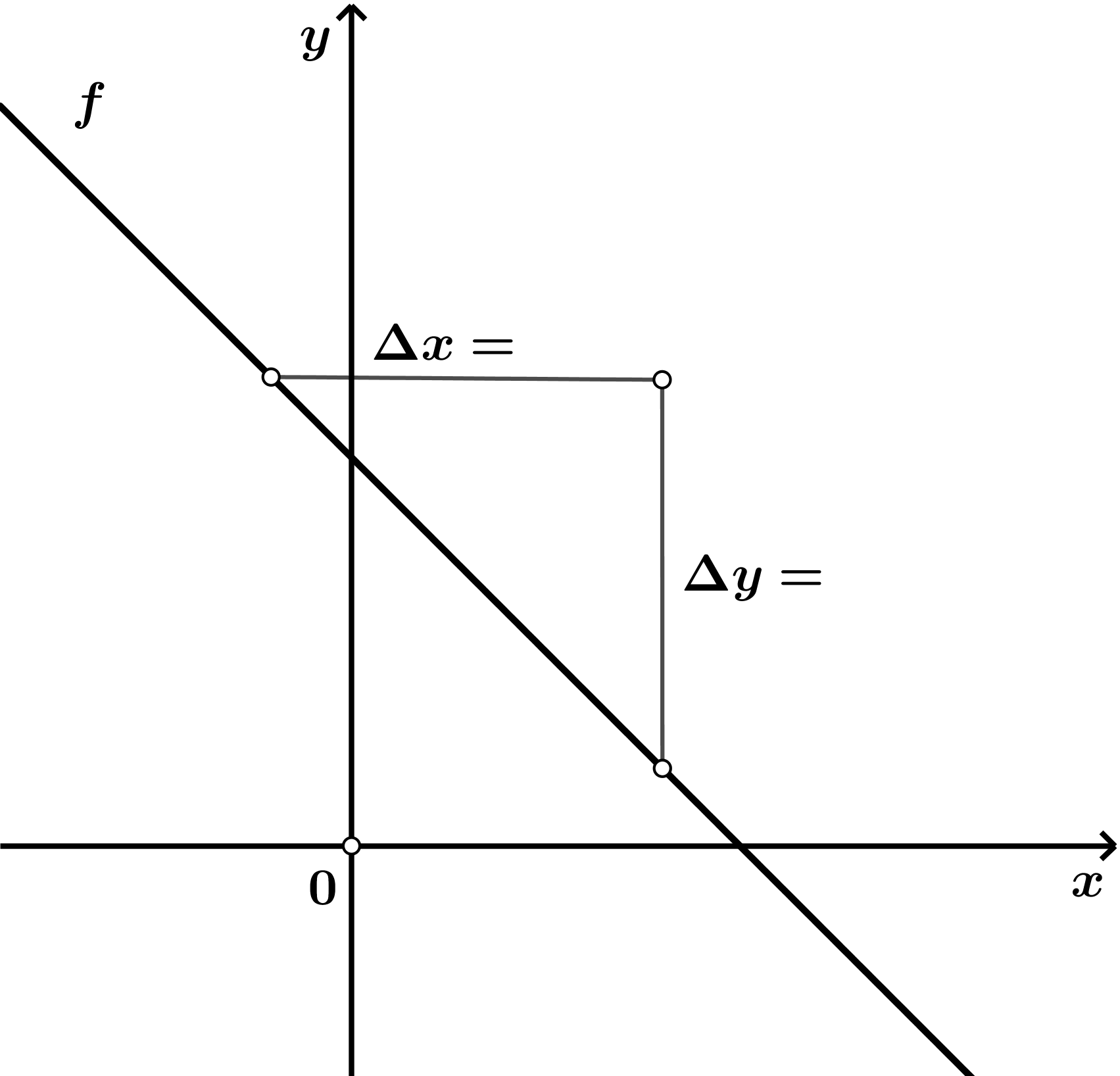
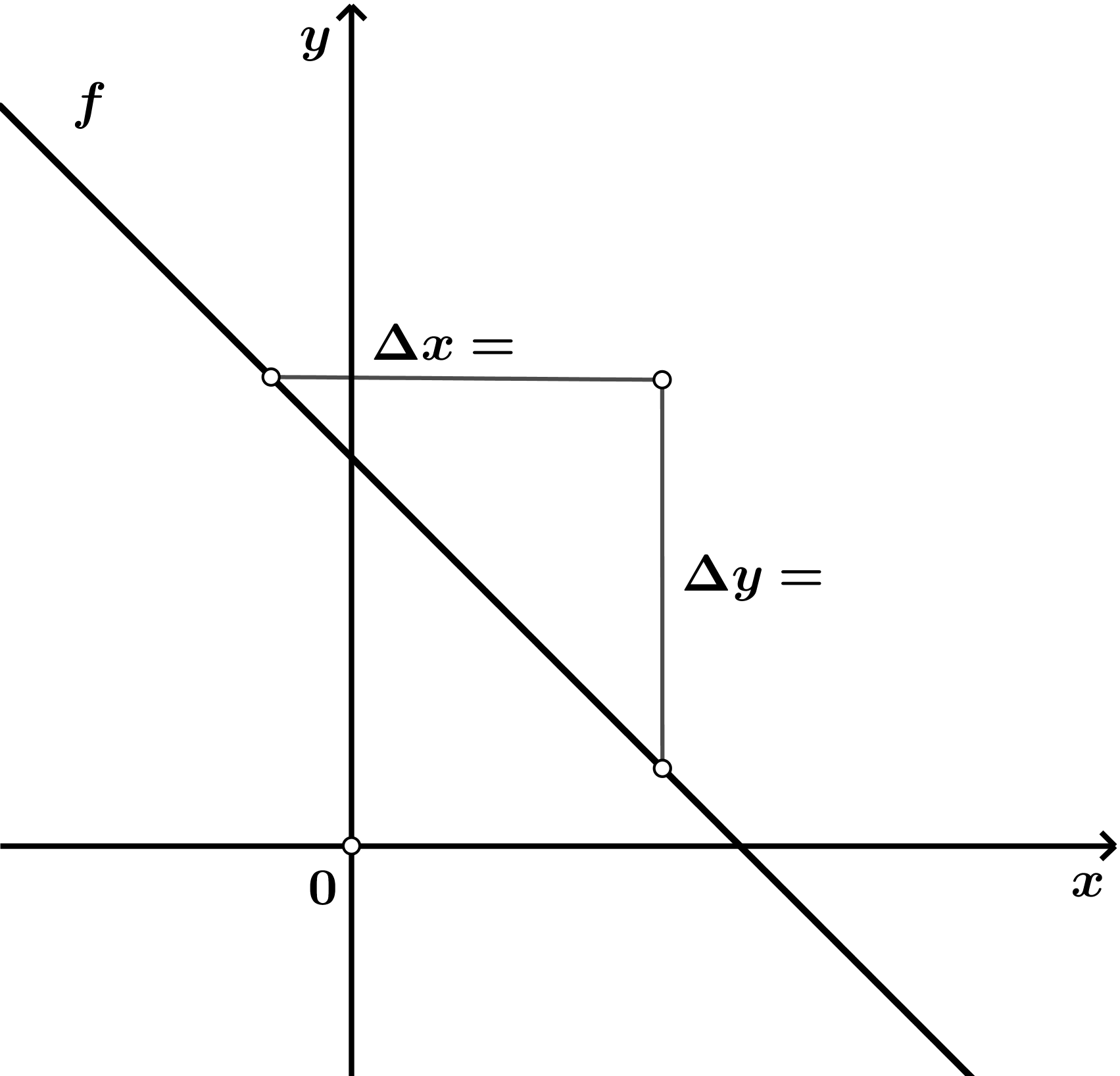
U koordinatnom je sustavu nacrtan graf linearne funkcije
Smjestite ponuđene vrijednosti na odgovarajuća mjesta.
Funkcija apsolutne vrijednosti zadana je pravilom pridruživanja Za koje vrijednosti argumenta je
Ovisnost duljine čeličnog snopa linearno je ovisna o temperaturi. Pri temperaturi od duljina je čelika metara, a pri temperaturi od duljina je istoga snopa metara. Koje od navedenih pravila pridruživanja opisuje ovisnost duljine čeličnog snopa o temperaturi