

U jednoj su trgovini cipela istraživali koja se veličina cipela najviše prodaje pa su dva puta bilježili veličine uzastopno prodanih cipela. Rezultati su prikazani odgovarajućim stupčastim dijagramima.
Prosječna veličina cipela koje su se prodale prijepodne iznosi I prosječna veličina cipela koje su se prodale poslijepodne iznosi To bi moglo značiti da su prodaje skoro jednake. Međutim, iz stupčastih dijagrama vidimo da postoji razlika.
Što možemo zaključiti?
Da bismo dobro opisali skup podataka, nije dovoljno znati njegovu mjeru srednje vrijednosti, već i raspršenost podataka.
Krenimo redom.
Raspon podataka je razlika između najveće i najmanje vrijednosti podataka.
Primjer 1.
Na jednome su testiranju dobiveni sljedeći rezultati:
Uočimo da je najmanji rezultat a najveći Dakle, raspon podataka je
Raspon podataka vrlo je gruba mjera raspršenosti, jer nam ne govori ništa o podatcima koji se nalaze između najmanje i najveće vrijednosti podataka.
Za daljnje proučavanje podataka uvedimo još neke važne pojmove.
Znatno će bolja mjera raspršenosti biti raspon središnjih
podataka.
Već ste upoznali medijan, vrijednost koja skup podataka dijeli na dva jednaka dijela. Ti se dijelovi dalje dijele na dva jednaka dijela, tj. četvrtine pomoću kvartila.
Prvi ili donji kvartil je broj od kojega je podataka manje ili je njemu jednako.
Drugi je kvartil medijan.
Treći ili gornji kvartil je broj od kojega je
podataka manje ili je njemu jednako.
Pogledajmo u animaciji kako ćemo odrediti kvartile za skup podataka
Interkvartilni raspon je razlika između gornjeg i donjeg kvartila, tj.
Za skup podataka interkvartilni raspon je

Udruga potrošača istraživala je trajanje dviju različitih vrsta baterija A i B. Testirano je po komada svake vrste. Dobiveni su sljedeći rezultati:
| Vrsta baterije |
Medijan (u satima) |
Gornji kvartil (u satima) |
Interkvartilni raspon (u satima) |
|---|---|---|---|
| A |
|
||
| B |
|
|
Koja je vrsta baterije pouzdanija?
Baterije vrste B su pouzdanije.
baterija vrste B ima vrijeme trajanja dulje od
sati, dok manji postotak baterija vrste A ima trajanje dulje od
sati (
baterija vrste A ima vrijeme trajanja dulje od
sati).
Pogledajmo kako ove podatke (najmanja vrijednost, najveća vrijednost, medijan, donji i gornji kvartil) možemo prikazati dijagramom.
Za crtanje dijagrama brkata kutija potrebno je odrediti najmanju vrijednost među podatcima donji kvartil medijan gornji kvartil i najveću vrijednost
Tih pet brojeva čini karakterističnu petorku skupa podataka.
Primjer 2.
Matija je u ovoj košarkaškoj sezoni postigao sljedeći broj koševa po utakmici:
Prikažimo podatke brkatom kutijom.
Prvo ćemo podatke poredati po veličini, da bismo odredili karakterističnu petorku.
Vidimo da je najmanja vrijednost a najveća vrijednost
Odredimo medijan te donji i gornji kvartil.
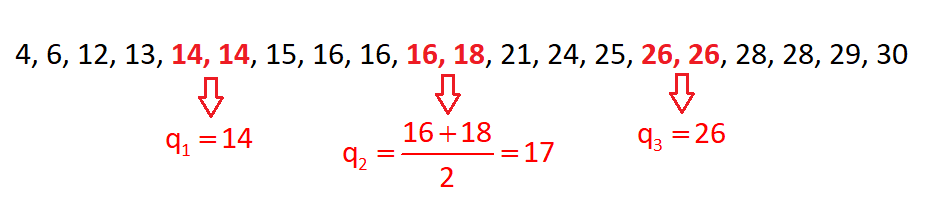
Nacrtajmo brojevni pravac i na njemu označimo točke koje pripadaju karakterističnoj petorki te ucrtajmo odgovarajući pravokutnik s "brkovima".
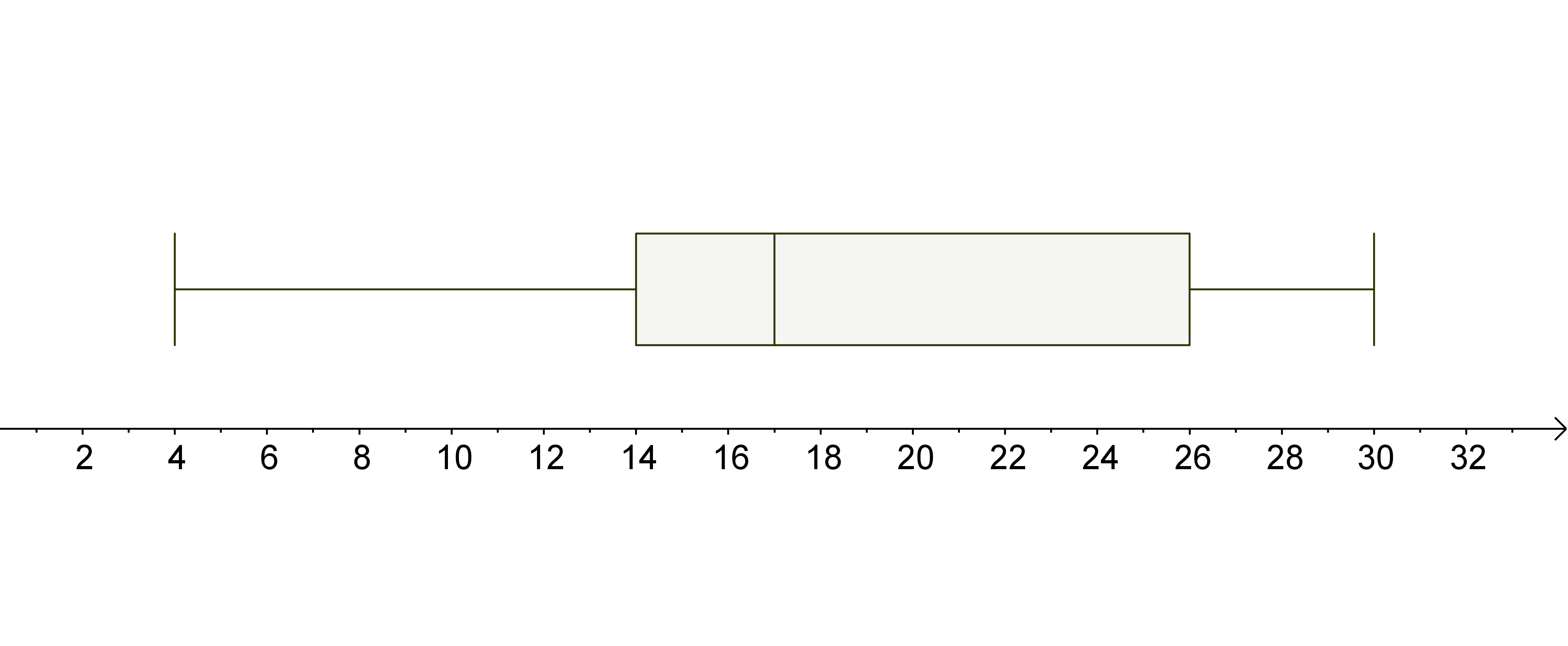
Standardna devijacija najbolja je mjera raspršenosti podataka. Ona se, za razliku od raspona i interkvartilnoga raspona, računa iz svih dobivenih podataka i najčešće se koristi za analizu podataka.
Neka su zadani podatci i neka je aritmetička sredina tih brojeva. Broj nazivamo odstupanje vrijednosti podatka od aritmetičke sredine.
Standardna devijacija za niz podataka
korijen prosječnog kvadratnog odstupanja vrijednosti podataka od aritmetičke sredine, tj.
Primjer 3.
Izračunajmo standardnu devijaciju za skup podataka
Prvo izračunajmo aritmetičku sredinu podataka
Sada je
Standardna devijacija izražava se u istim jedinicama kao i vrijednosti podataka.
Ponekad je lakše i preglednije standardnu devijaciju računati koristeći tablice.
Izračunajmo tako standardnu devijaciju za skup podataka
Prvo ćemo izračunati aritmetičku sredinu
Podatke ćemo smjestiti u tablicu.
| Vrijednosti | Frekvencija
|
|
|
|---|---|---|---|
|
|
|
||
|
|
|||
|
|
|||
| Ukupno |
Vidimo da zbroj u posljednjem stupcu iznosi
Tada je
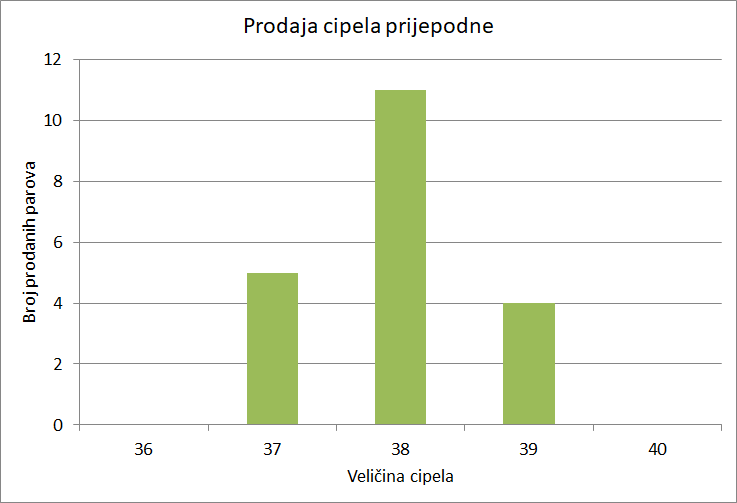
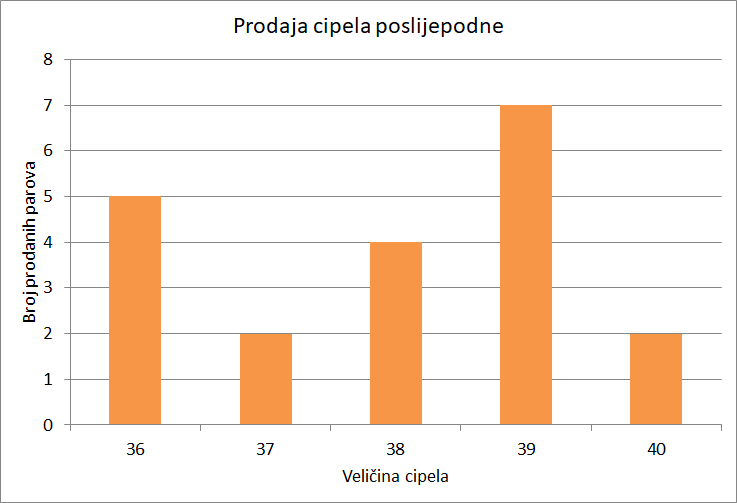
Istraživanje je pokazalo da veličina cipela koje se prodaju prijepodne varira nego veličina cipela koje se prodaju poslijepodne.
Pogledajmo kako za računanje i grafičko prikazivanje podataka možemo rabiti računalni program Excel koji je dio paketa Office 365 te je dostupan učenicima.
Pri računanju mjera srednjih vrijednosti i raspršenosti:
Upišite podatke u tablicu.
Postavite se na praznu ćeliju pa otvorite karticu Formule.
Pri grafičkom prikazu podataka:

Percentili
Percentili dijele skup podataka na dijelova, tj. svaki dio sadrži podataka. Percentil može biti bilo koji cijeli broj između i Percentil je vrijednost ispod koje se nalazi odgovarajući postotak svih podataka. Medijan, kao podatak koji se nalazi točno na sredini, jednak je percentilu.
Percentil nije isto što i postotak. Na primjer, ako se nečiji rezultat nalazi na
percentilu, to znači da
učenika ima lošiji rezultat od njega, a ne da je on točno riješio
testa.
Na školskoj su zadaći iz matematike učenici 1. a razreda postigli sljedeće bodove:
Želimo izračunati percentil.
Prvo bodove poredamo po veličini:
Ukupno ima rezultata.
Da bismo odredili koji se rezultat nalazi na nekom percentilu, trebamo izračunati poziciju tog percentila u nizu podataka prema formuli gdje je pozicija traženog percentila, traženi percentil, a ukupni broj podataka.
U našem je primjeru
Ovaj broj zaokružimo na prvi veći cijeli broj, to je
Zaključimo: Podatak na 9. mjestu, odnosno
bodova odgovara
percentilu, što znači da je
učenika 1. a razreda postiglo
ili manje od
bodova, a
učenika postiglo je
ili više bodova na ovoj školskoj zadaći.
Izračunajte
i
percentil danih bodova.
Pozicija pecentila je što znači da broj bodova odgovara percentilu.
Pozicija
percentila je
što znači da broj bodova
odgovara
percentilu.

Razbijači šifara
Razbijači šifara uvelike koriste statistiku. Poznato je da se neka slova češće pojavljuju nego neka druga.
Koje se slovo hrvatske abecede najčešće pojavljuje? Koji samoglasnik, a koji suglasnik?
Odaberite novinski članak od otprilike
riječi pa odredite frekvencije slova. Odredite raspršenost po raznim kriterijima.
Što je od navedenoga točno za niz podataka
Na slici je prikazana brkata kutija. Označite karakterističnu petorku na osi
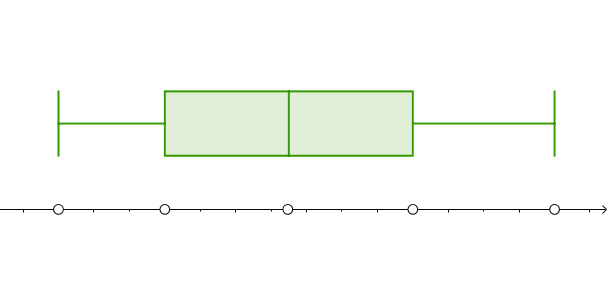
Gornji kvartil
Maksimum
Medijan
Minimum
Donji kvartil
Tri skupine učenika sudjelovale su u ispitivanju u kojemu je bilo moguće skupiti najviše bodova. U sve je tri skupine aritmetička sredina postignutih bodova jednaka ali se razlikuju po raspršenosti podataka. Rezultati su prikazani stupčastim dijagramima.
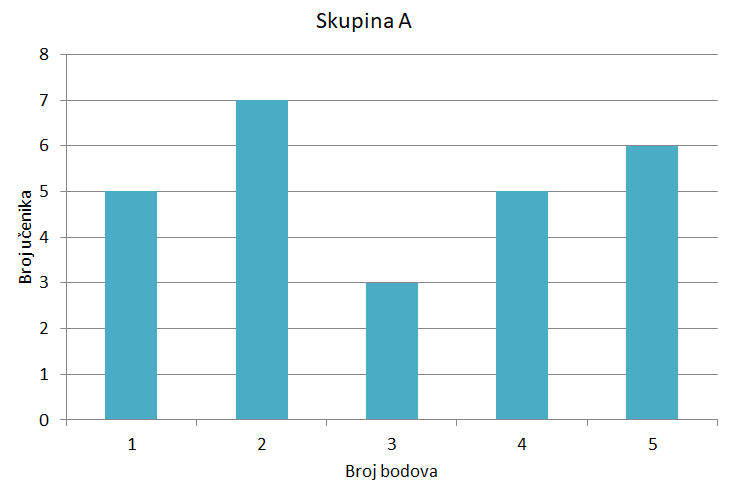
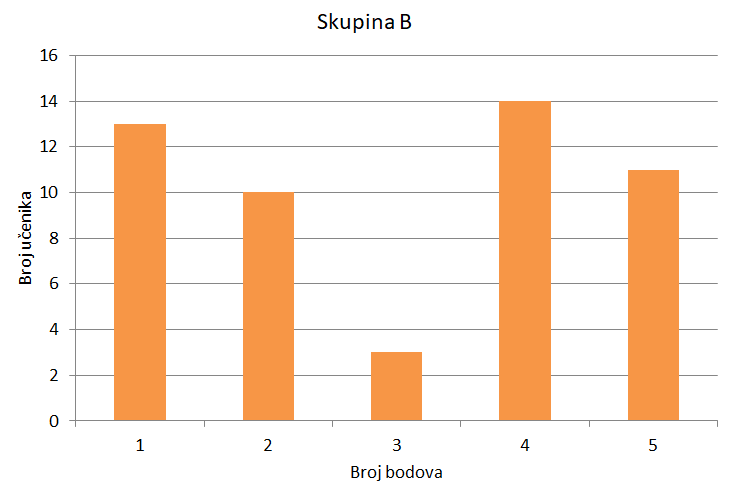
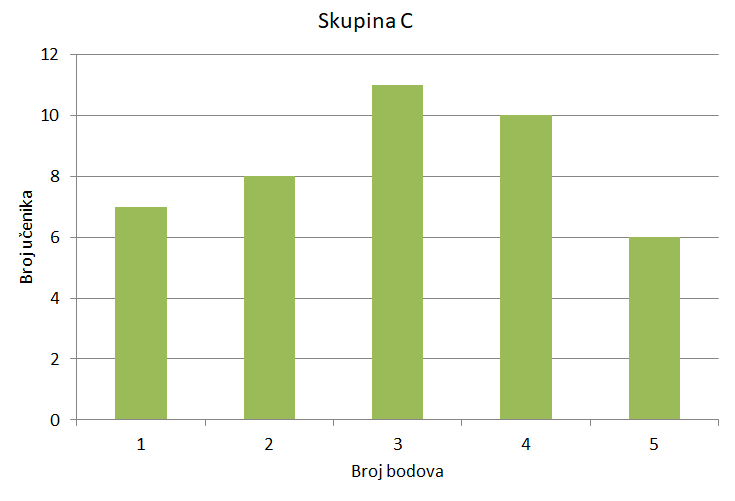
Na Masters teniskom turniru u Madridu 2017. godine Borna Ćorić odigrao je šest mečeva. Postotci dobivenih poena osvojenih na prvome servisu na tome turniru dani su u tablici.
| Broj meča | ||||||
| osvojenih poena na prvome servisu |
Kolika je standardna devijacija?