


Ima li učenik Vedran pravo? Proučimo.
Podsjetimo se što je geometrijska sredina dvaju brojeva.
Neka su pozitivni realni brojevi. Broj jest geometrijska sredina brojeva i ako i samo ako vrijedi
To još drugačije zapisujemo
Pogledajte animaciju.
Ponovite korake iz animacije rezanjem trokuta od papira.
Što zaključujete? Uočavate li sličnost trokuta?
Primjer 1.
Obrazložimo postupak rezanja trokuta matematičkim jezikom.
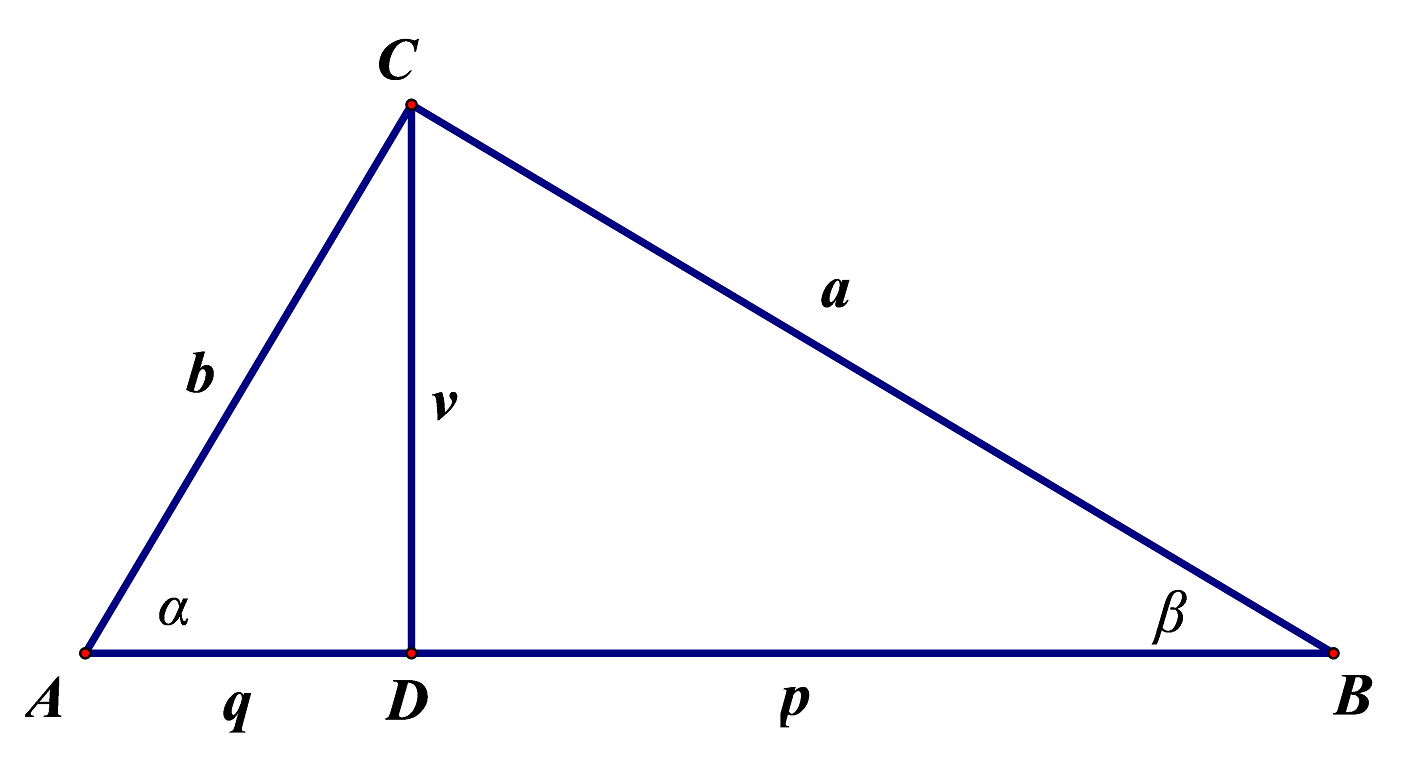
Neka je pravokutni trokut duljine kateta i i duljina hipotenuze
Označimo s
nožište visine spuštene na hipotenuzu trokuta, a s
i
ortogonalne projekcije kateta na hipotenuzu te kutove
i
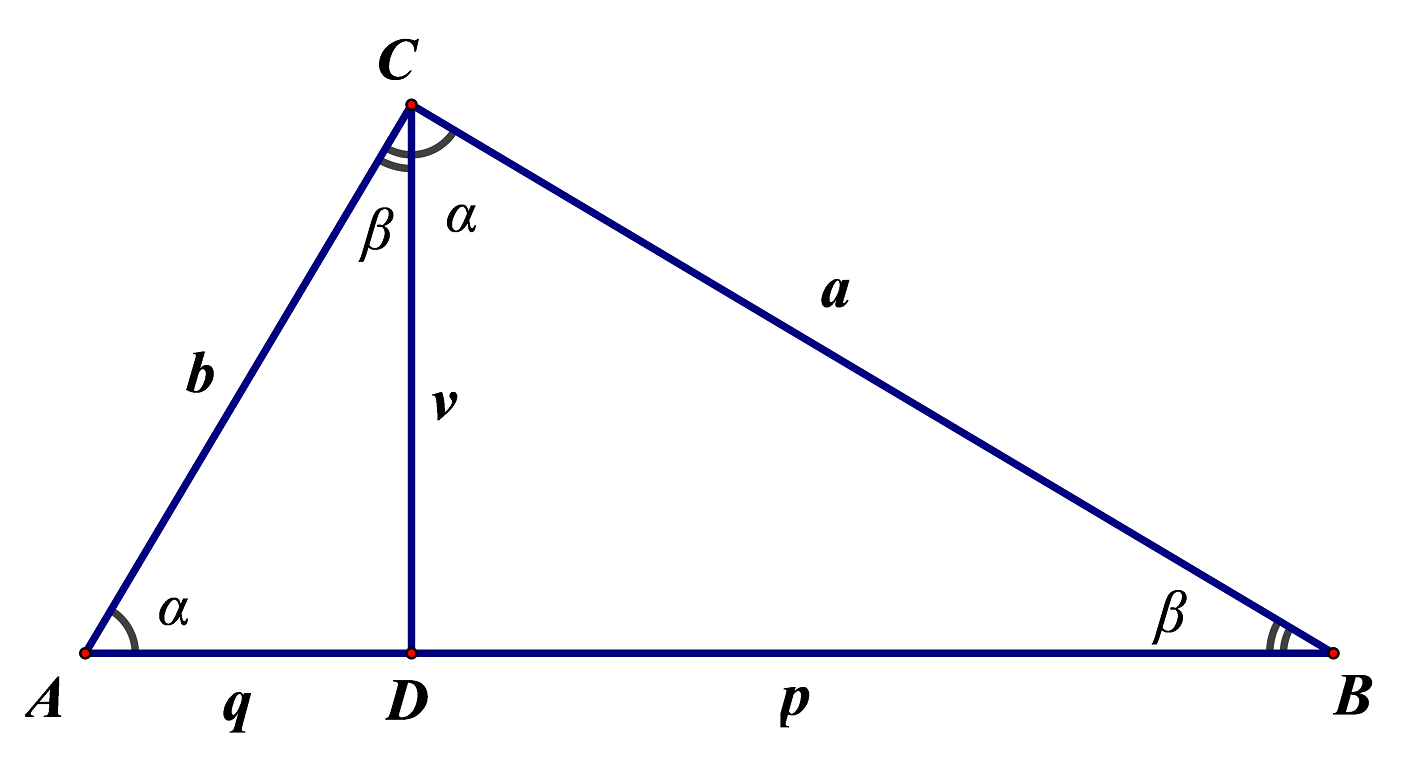
Uočimo sukladne kutove.
Mjera kuta pa je mjera kuta što je jednako Slično je mjera kuta
Na slici su označeni sukladni kutovi. Trokuti i imaju sva tri kuta sukladna. Prema definiciji sličnosti trokuta sva su tri trokuta slična.
Iz slijedi da je odnosno
Usporedimo li ovaj izraz s Vedranovom tvrdnjom na početku, vidimo da je imao pravo.
Neka su i katete, a hipotenuza pravokutnog trokuta i neka je nožište visine spuštene iz vrha na hipotenuzu. Neka su i duljine ortogonalnih projekcija kateta na hipotenuzu. Tada vrijedi:
Na isti način izvedite preostale dvije tvrdnje pomoću sličnih trokuta.
Iz
slijedi da je
odnosno
Iz
slijedi da je
odnosno
Vrijedi li obrat Euklidovog poučka?
Ako je točka nožište visine trokuta spuštene iz vrha i vrijedi da je možemo li zaključiti da je trokut pravokutan?
Provjerite.
Pročitajte više na http://mis.element.hr/fajli/526/04-08.pdf.
U pravokutnom je trokutu
a
Izračunajte duljine kateta toga trokuta i duljinu visine na hipotenuzu.
Odredite površinu pravokutnog trokuta ako je
Odredite duljine stranica pravokutnog trokuta ako je

Tena tvrdi da pomoću bilježnice iz matematike, koristeći Euklidov poučak, može približno izračunati visinu žirafe u zoološkom vrtu. Kako?
Tena je visoka a žirafa je visoka oko metara. Na kojoj udaljenosti od žirafe Tena mora stajati da bi izmjerila njezinu visinu?
Na udaljenosti od oko
metara.
Ako u pravokutnom trokutu na slici vrijedi da je
označite pravilno preostale vrhove trokuta.
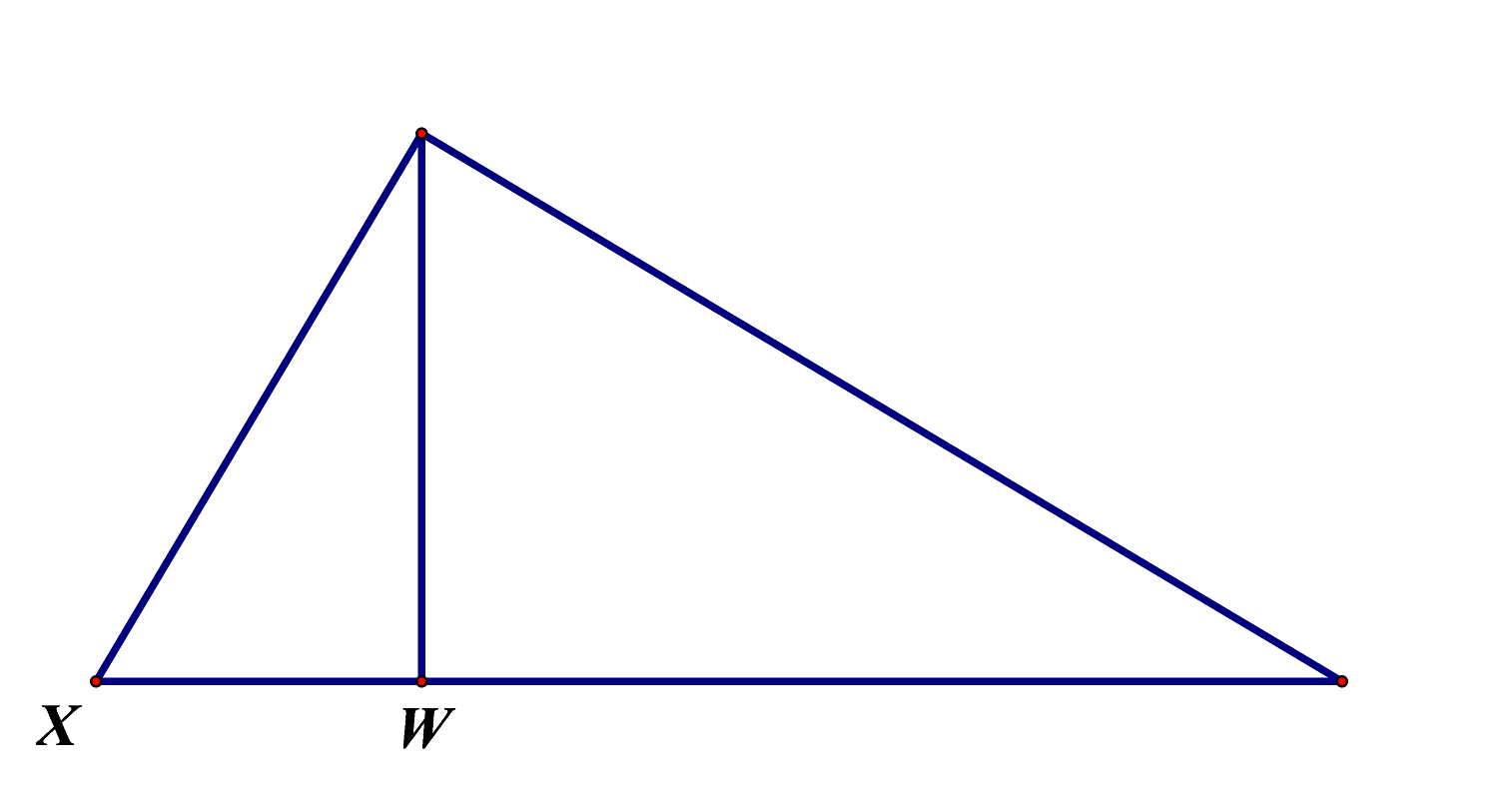
Y
Z
Nožište visine na hipotenuzu pravokutnog trokuta dijeli tu hipotenuzu na dijelove čije su duljine u omjeru
Kolika je duljina hipotenuze trokuta ako je površina trokuta jednaka
Duljina jedne katete pravokutnog trokuta iznosi
a duljina visine na hipotenuzu jest
Opseg toga trokuta jest