Početna veličina slova
Na samom početku prirodno je upitati se kakve veze pojam tok ima s linearnom funkcijom. Rijeka teče, kreće se, ima svoj tok; automobil se kreće, često nailazi na kružni tok... kreće li se na neki način i linearna funkcija?
Kreće li se, dakle, linearna funkcija?
Pogledajmo što o kretanju linearne funkcije kažu Iskra i profesor Bistrić.
Odrediti tok linearne funkcije znači odrediti je li ona rastuća ili padajuća funkcija.
Istražimo o čemu ovisi tok funkcije.
Primjer 1.
Uz sljedeću interakciju istražite o čemu ovisi tok funkcije. Mijenjajte položaj klizača i pokušajte dati odgovor na postavljena pitanja.
Postoji li veza između vrijednosti parametara funkcije i njezina toka?
Mora li funkcija uvijek biti ili rastuća ili padajuća?
Provjerimo kroz kratki kviz izvedene zaključke. Ako niste sigurni u odgovor, vratite se na interakciju i usmjerite pozornost na sadržaj pitanja.
Tok linearne funkcije
Linearna funkcija
je ako je njezin koeficijent smjera
Ako je koeficijent smjera
linearna funkcija je .
Pomoć:
Proučite aplet još jedanput, a pažnju usmjerite na predznak parametra
Postoji li položaj u kojemu funkcija nije niti padajuća niti rastuća?
Pomoć:
Vratite se proučavanju apleta. Polako mijenjajte položaj klizača Posebnu pozornost usmjerite na trenutak kada funkcija iz rastuće prelazi u padajuću, ili obrnuto.
Funkcija je stalna ili konstantna ako je njezin nagib:
Iz padajućeg izbornika odaberite odgovarajući pojam.
Iz padajućeg izbornika odaberite odgovarajući pojam.
Iz padajućeg izbornika odaberite odgovarajući pojam.
Spojite parove tako da tvrdnja bude istinita.
|
Ako je nagib pravca negativan broj,
|
funkcija je rastuća. |
|
Ako je nagib pravca pozitivan broj,
|
funkcija je padajuća. |
|
Ako je nagib pravca jednak nuli,
|
funkcija je konstantna. |
Ako za bilo koji argument funkcija ima uvijek istu vrijednost, ona je funkcija.
Odredite tok zadanih funkcija.
Pomoć:
Pažljivo odredite koeficijente.
Linearna funkcija kojoj je koeficijent smjera pozitivan, rastuća je funkcija.
Linearna funkcija kojoj je koeficijent smjera negativan, padajuća je funkcija.
Primjer 2.
Graf linearne funkcije siječe obje koordinatne osi. Što možemo reći o koordinatama tih sjecišta?
Uz danu interakciju prisjetite se pojmova:
- sjecište pravca s -osi
- nultočka funkcije
- sjecište pravca s -osi i
- odsječak na osi ordinata.
Provjerite svoje znanje očitavanja koordinata sjecišta s koordinatnim osima.
Zadana je linearna funkcija
Da bismo odredili koordinate sjecišta pravca s -osi, dovoljno je poznavati jednadžbu pravca ili formulu linearne funkcije.
Pravac siječe os ordinata u točki koja je zadana koordinatama:
Pomoć:
Svaka točka na osi ordinata ima prvu koordinatu jednaku nuli.
Parametar određuje odsječak na osi ordinata.
Zadana funkcija je
Graf linearne funkcije siječe os apscisu u točki čija je uvijek nula.
Nultočku funkcije određujemo tako da:
Izračunajte ili očitajte tražene vrijednosti i odredite parove.
|
sjecište s
-osi
|
|
|
nultočka
|
|
|
sjecište s
-osi
|
|
|
odsječak na
-osi
|
Primjer 3.
Nacrtajte graf linearne funkcije tako da prvo odredite sjecišta s koordinatnim osima. Crtati možete u bilježnicu ili se koristiti pripremljenim predloškom.
Za određivanje sjecišta grafa funkcije s
-osi potrebno je iz jednadžbe očitati odsječak na osi ordinata i zapisati ga kao ordinatu točke, tj.
jer je apscisa točke uvijek nula.
Za određivanje sjecišta s apscisom treba riješiti jednadžbu jer je ordinata točke uvijek nula.
Rješenje jednadžbe je
pa je sjecište s apscisom točka
Zadanim dvjema točkama možemo nacrtati pravac.
Svoje rješenje možete provjeriti na drugi način: u predlošku za crtanje pravaca u polje za unos upišite jednadžbu pravca, a pri zapisu razlomka umjesto razlomačke crte upotrijebite oznaku Kako u zapisu ne bi ostao u nazivniku, nakon upisivanja nazivnika upotrijebite desnu strjelicu na tipkovnici. Ako ste zadatak riješili točno, zadani pravac podudarat će se s pravcem koji ste nacrtali.
U interakciji je zadana jednadžba pravca. Nacrtajte zadani pravac tako da prvo računski odredite sjecišta pravca s koordinatnim osima.
Točnost svoga rješenja možete provjeriti tako da u predlošku za crtanje pravaca odaberete rješenje. Ako ste zadatak točno riješili, zadani pravac podudarat će se s pravcem koji ste nacrtali. Ako vaše rješenje nije točno, vidjet ćete dva pravca u koordinatnom sustavu.
Zadatak možete ponavljati sve dok ga ne uvježbate.
O nagibu pravca već smo govorili. Sada ćemo, nakon što ponovimo poznate činjenice, istražiti kako pomoću nagiba i odsječka na osi ordinata možemo pravac nacrtati u pravokutnom koordinatnom sustavu.
U zapisu formule linearne funkcije i u zapisu pripadajuće jednadžbe pravca nagib ima oznaku:
Primjer 4.
Proučimo nagibe danih pravaca u koordinatnom sustavu. Pratimo istodobno njihov položaj (međusobni i u samom koordinatnom sustavu) i zapis jednadžbe.
- Možete mijenjati položaj klizača koji su povezani s pravcem ljubičaste boje (zadani pravac).
- Preostali pravci imaju zadan odsječak na osi ordinata, ali imaju isti koeficijent smjera kao i zadani pravac.
- Odaberite nagib i pomoću klizača provjerite imaju li preostali pravci isti nagib (ako je nagib isti, pravci će se podudarati).
- Možete li naći vezu između duljina kateta trokuta koji određuje nagib pravca i koeficijenta
Provjerimo ispravnost zaključaka kroz kratki kviz.
Paralelni su oni pravci koji imaju isti:
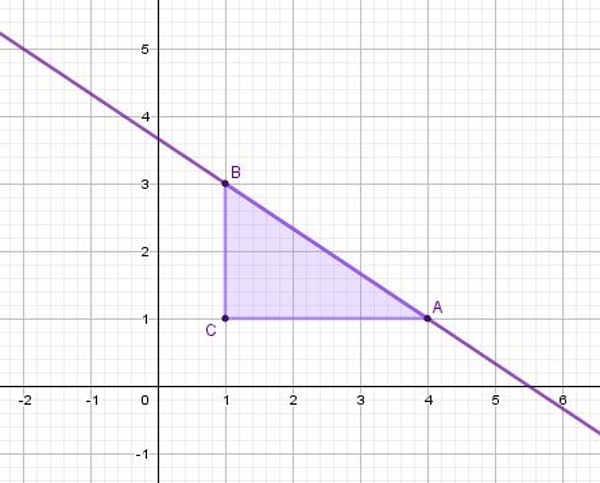
Koeficijent možemo izračunati pomoću pravokutnog trokuta čija hipotenuza pripada pravcu, kao na slici.
Pomoć:
Proučite još jedanput aplet.
Postupak:
Da bismo izračunali nagib, potrebno je duljinu vertikalne katete podijeliti s duljinom horizontalne i pritom naznačiti negativan predznak ako funkcija pada.
Odredite koeficijent smjera zadanoga pravca.
Pomoć:
Pravac je graf rastuće funkcije pa je koeficijent pozitivan.
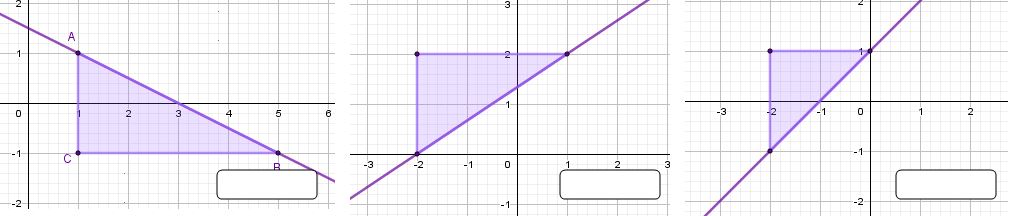
Zadanim pravcima pridružite pripadajuće nagibe.
Pomoć:
Razlomak treba biti neskrativ.
Uz sljedeću interakciju uvježbajte očitavanje nagiba, ali i odsječka na -osi. Ne zaboravite uvijek provjeriti je li funkcija rastuća ili padajuća - zbog predznaka.
Pomoćni pravokutni trokut čije su katete usporedne s koordinatnim osima neka, radi jednostavnosti, ima cjelobrojne koordinate vrhova šiljastih kutova.
Nakon što smo uvježbali očitati koeficijent smjera pravca, istražit ćemo još jedno njegovo svojstvo, povezano s brzinom rasta ili pada. Primijetili smo da su neki pravci iznimno strmi, a neki imaju blagi uspon, odnosno - neke funkcije padaju brže od drugih, neke sporije rastu. Istražimo.
Primjer 5.
Zadana su dva pravca u pravokutnom koordinatnom sustavu u ravnini.
- Mijenjajte položaj klizača nagiba za oba pravca i istražite kako strmina pravca ovisi o vrijednosti koeficijenta smjera.
- Kakav je nagib kada je pravac najstrmiji?
- Ima li razlike ovisno o predznaku nagiba?
Provjerimo zaključke kroz kratki kviz. Uspoređujemo li dvije rastuće linearne funkcije, brže raste ona koja ima koeficijent smjera.
Uspoređujemo li dvije padajuće linearne funkcije, brže pada ona koja ima koeficijent smjera.
Sljedeći pojmovi odnose se na graf linearne funkcije u koordinatnom sustavu u ravnini. Uparite odgovarajuće.
|
Strmiji pravac
|
funkcija sporije raste ili pada |
|
Blaži nagib pravca
|
funkcija brže raste ili pada |
Poredajte zadane jednadžbe pravca tako da na prvom mjestu bude ona koja pripada funkciji koja najbrže raste, a na zadnjem ona koja raste najsporije.
Pomoć:
Zamislite da se penjete po pravcu. Onaj koji je najstrmiji, na kojem biste se najteže kretali, taj najbrže raste.
Ili, prisjetite se zaključka o koeficijentu smjera.
Usporedite brzinu pada danih funkcija i uparite ih tako da tvrdnje budu istinite.
|
Najbrže pada
|
|
|
Najsporije pada
|
|
|
Pada
|
|
Pomoć:
Brže pada ona linearna funkcija koja ima manji koeficijent smjera.
Postupak:
; Najbrže pada funkcija čiji je koeficijent najmanji.
Brže raste ona linearna funkcija koja ima veći koeficijent smjera.
Brže pada ona linearna funkcija koja ima manji koeficijent smjera.
Razmislite na koji biste način mogli pomoću koeficijenata (nagiba i odsječka na osi ordinata) nacrtati pravac kojemu je zadana jednadžba.
Istražujući svojstva koeficijenta smjera linearne funkcije, primijetili smo da u slučaju kada je funkcija niti raste niti pada. Vrijednosti tako zadane funkcije ne mijenjaju se kod promjene argumenta, nego je za svaki argument vrijednost funkcije ista.
Vrijednost funkcije ne ovisi linearno o argumentu i zato više ne možemo govoriti o linearnoj funkciji.
No, i takva funkcija ima graf koji je pravac.
Primjer 6.
Nacrtajte pravac zadan formulom . Kako glasi jednadžba nacrtanog pravca?
Crtati možete u bilježnicu ili se možete koristiti predloškom za crtanje pravaca.
Nakon što ste odredili tražene vrijednosti u tablici, alatom Točka odredite položaj točke u koordinatnom sustavu, a zatim s pomoću alata Pravac nacrtajte pravac.
Jednadžba pravca glasi pri čemu je odsječak na osi ordinata.
Općenito, ako je u formuli funkcije
parametar
jednadžba ima oblik
Jednadžba pravca usporednog s -osi jest pri čemu je odsječak na osi ordinata.
Primjer 7.
Nacrtajmo u koordinatnom sustavu pravac koji je usporedan s osi ordinata i uočimo koordinate točaka koje mu pripadaju.
Ako je zadana linearna funkcija ili pripadna jednadžba pravca, pravac možemo nacrtati pomoću:
Prva dva načina smo dobro usvojili, a oni koji to žele, mogu upoznati i ovaj treći način koji je ujedno i najbrži način za crtanje pravaca u pravokutnom koordinatnom sustavu. Postupak "brzog" crtanja pravca u koordinatnom sustavu, pomoću parametara jednadžbe pravca, možete naučiti uz pomoć interakcije autorice Željke Dijanić.
