

Upoznavanjem linearne funkcije i njezina grafa napravili smo izuzetno važan iskorak u učenju matematike. Ideju o povezivanju geometrije i jednadžbi razvijali su neovisno jedan o drugome francuski matematičari Rene Descartes i Pierre de Fermat.
Pravac, koji je dosad bio samo ravna beskonačna crta, postao je skup svih točaka čije koordinate zadovoljavaju neku jednadžbu. I to ne bilo kakvu jednadžbu, nego baš onu koja opisuje linearnu funkciju. Polako, stupili smo na tlo analitičke geometrije, grane matematike koja će nas pratiti tijekom školovanja.
Saznajte nešto više o životu i radu dvojice spomenutih francuskih matematičara. Istražite čime su se bavili i to prezentirajte (one dijelove koje možete razumijeti) ostalim učenicima u razredu. Koje su poznate osobe iz svijeta znanosti bile njihovi suvremenici?
Kroz početni kviz možete ponoviti osnovne pojmove povezane s linearnom funkcijom i njezinim grafom, a za uvježbavanje vam predlažemo nekoliko zadataka koje možete samostalno riješiti u bilježnici ili u nekom interaktivnom elementu. Zadnjih nekoliko zadataka je za one koji žele znati malo više, ali svi ih možete pokušati riješiti. Nakon što riješite zadatke, usporedite svoja rješenja s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili zamolite za pomoć ako vam je neki od zadataka težak.
Zadana je linearna funkcija pri čemu je Proučite ponuđene pojmove i spojite odgovarajuće.
|
argument
|
|
|
vrijednost funkcije
|
|
|
odsječak na
-osi
|
|
|
koeficijent smjera ili nagib
|
|
Argument linearne funkcije je
Pomoć:
Vrijednost funkcije ovisi o argumentu i pravilu pridruživanja.
Pomoć:
Tok funkcije zamišljamo kao kretanje funkcije. Ako je za svaki sljedeći (veći) argument i vrijednost funkcije veća, funkcija raste. U suprotnom je funkcija padajuća.
Linearna je funkcija
Pomoć:
Tok funkcije određen je koeficijentom smjera. Ako je koeficijent smjera pozitivan broj, funkcija je rastuća.
Postupak:
Rastuća je jer je
Ako dva pravca imaju isti nagib, kažemo da su pravci .
Pomoć:
Proučite još jedanput jedinicu10.5. Tok linearne funkcije i istraživački aplet o nagibu pravca.
Koji je od ponuđenih pravaca usporedan s grafom linearne funkcije
Pomoć:
Usporedni pravci imaju isti koeficijent smjera ili nagib pravca.
Postupak:
Pravac čija je jednadžba jedini ima koeficijent smjera jednak zadanome, tj.
Koja od ponuđenih jednadžbi pripada pravcu koji je usporedan s osi
Pomoć:
Pravac je usporedan s apscisom ako za svaki argument ima istu vrijednost funkcije, tj. vrijednost funkcije ne ovisi o odabiru broja

Istražite temperaturne skale koje se, uz Celzijevu, i danas koriste u svijetu. Prikažite njihovu međusobnu ovisnost grafički, formulom i tablicom.
Računske zadatke riješite u bilježnici, a odgovore na teorijska pitanja pokušajte zapisati pazeći na pravilan matematički izražaj.
Za zagrijavanje riješite ove jednostavne zadatke i zabavite se otkrivanjem slike.
Što zapravo znači odrediti eksplicitnu jednadžbu nekog pravca?
Odrediti eksplicitnu jednadžbu pravca znači zapisati jednadžbu pravca u obliku pri čemu moramo znati vrijednost koeficijenata i Dakle, iz zadanih podataka moramo izračunati vrijednost koeficijenata (parametara).
Odredite eksplicitnu jednadžbu pravca čiji je nagib jednak i koji prolazi točkom
Uvrstimo zadane vrijednosti u opći oblik eksplicitne jednadžbe pravca.
Jednadžba pravca glasi
Pridružite parove usporednih pravaca.
|
|
|
|
|
|
|
|
|
Pomoć:
Pravci su usporedni ako imaju jednake koeficijente smjera.
Što znači da točka pripada nekom pravcu u koordinatnom sustavu?
Točka pripada pravcu ako njezine koordinate zadovoljavaju jednadžbu pravca, tj. ako u jednadžbu pravca umjesto broja uvrstimo prvu koordinatu točke, a umjesto broja drugu koordinatu točke, dobit ćemo istinitu jednakost.
Napišite jednadžbu pravca koji prolazi točkama
i
Rješenje je dobivenog sustava pa jednadžba pravca glasi
Zadane jednadžbe pridružite odgovarajućim pravcima.
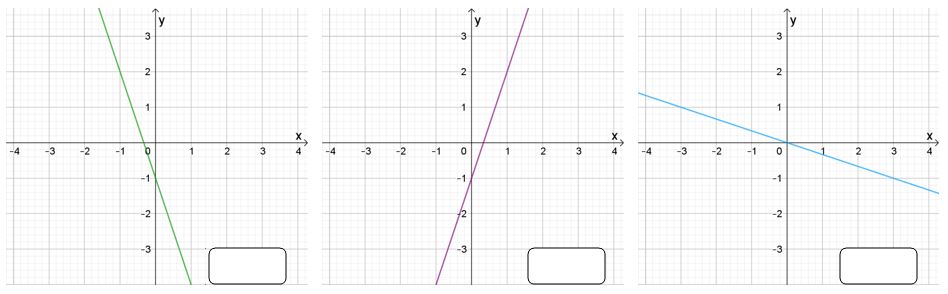
Pomoć:
Osnovni kriteriji su: odsječak na osi tok funkcije kojoj pravac pripada (rast ili pad) te nultočke.
Graf linearne funkcije je pravac čija je jednadžba Skicirajte pravac koji siječe obje koordinatne osi i napišite koordinate sjecišta.
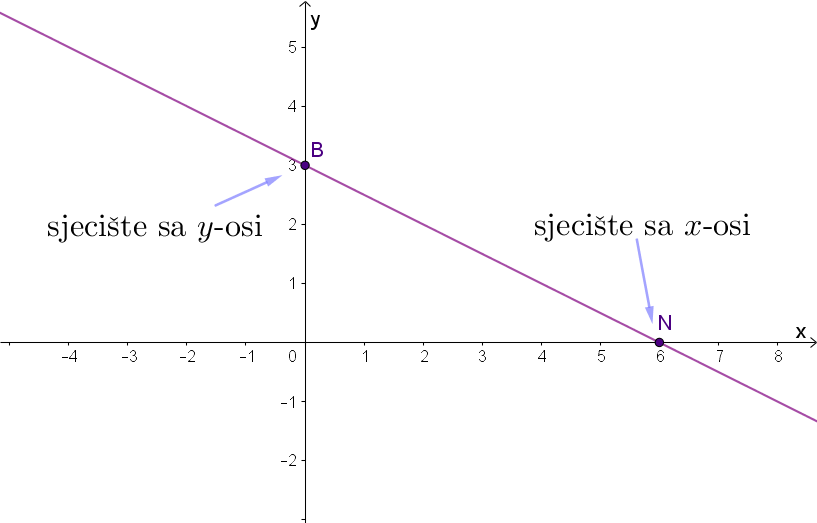
Sjecište s
-osi
dobijemo iz jednadžbe
(jer je za svaku točku na osi apscisa druga koordinata jednaka nuli).
Sjecište s
-osi je
(jer je
odsječak na osi ordinata).
U kojim točkama graf linearne funkcije siječe koordinatne osi? Riješite zadatak grafički i računski.
Crtati možete u bilježnicu ili možete koristiti ponuđeni predložak.
Za vježbu, umjesto zadane linearne funkcije možete sami zadati novu linearnu funkciju.
Dopunite tablicu.
Izračunajte površinu trokuta koji je omeđen koordinatnim osima i pravcem
Predlažemo da rješenje provjerite koristeći se predloškom za crtanje pravaca i algebarskim prozorom prateći sljedeće upute:
Napišite sustav linearnih jednadžbi koji:
Dani predložak može vam poslužiti za rješavanje ovog zadatka grafičkom metodom.
Rješenje ovog zadatka provjerite grafičkom metodom. U danom digitalnom predlošku nacrtajte pravce. Najjednostavnije ćete to učiniti izravnim upisivanjem jednadžbe u polje za unos.
Vaše je rješenje točno ako vrijedi:
Sestre blizanke, Ana i Sonja, željele bi kupiti novo prijenosno računalo koje košta nešto više od Dogovor s roditeljima je takav da će pola iznosa dati oni, a pola njih dvije ravnopravno. Za razliku od Sonje koja nema ništa, Ana ima ušteđevinu od te su procijenile da će biti dovoljno da Sonja štedi tjedno, a Ana
Prikažite grafički ovisnost iznosa ušteđevine o broju proteklih tjedana.

Nakon koliko će tjedana imati ušteđen isti iznos? Hoće li to biti dovoljno za njihovu polovinu cijene računala?
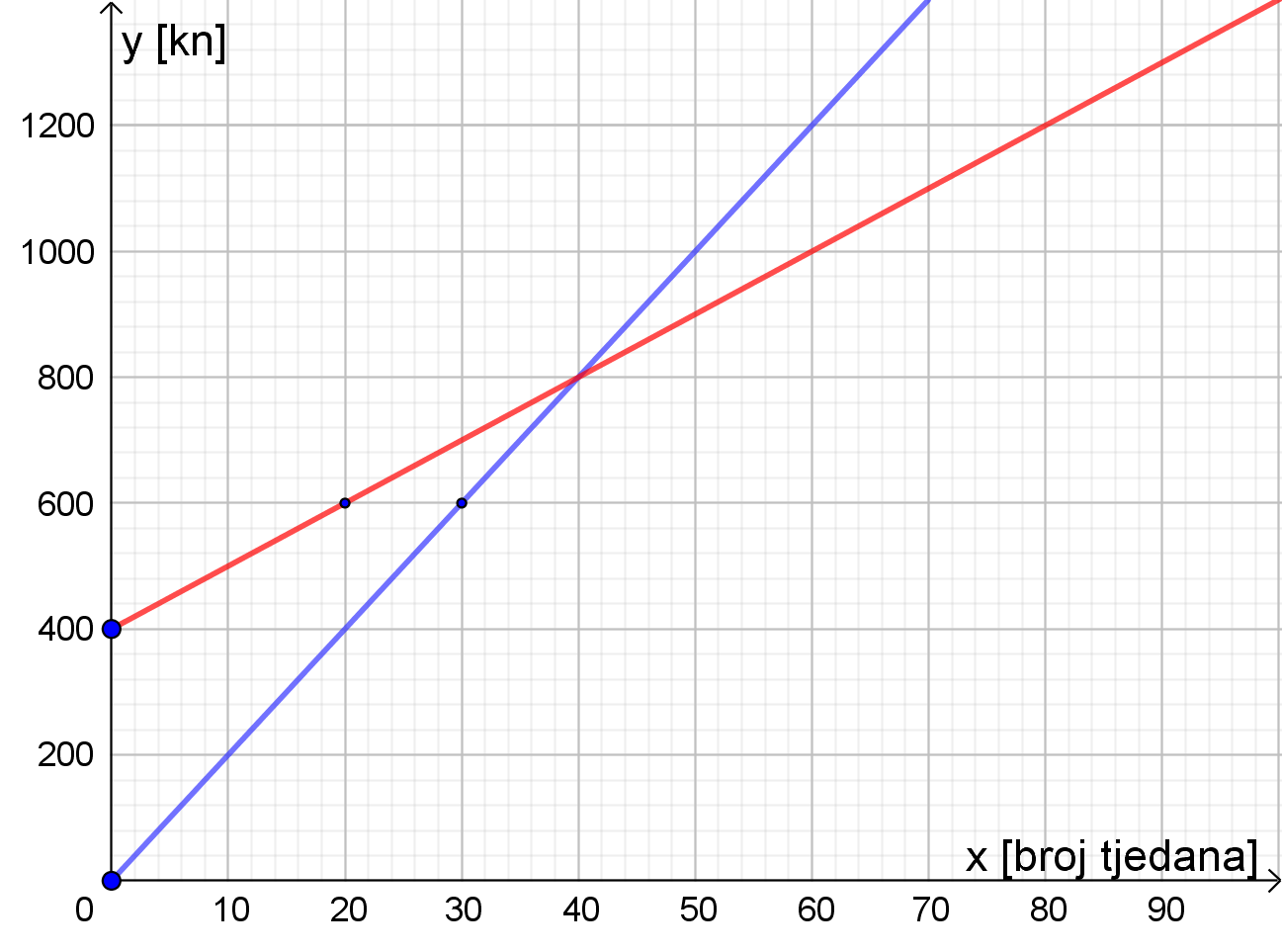
Proučite sliku.
Istražite tarife za mobilne usluge kojima se koristite vi i vaši ukućani. Koje se od njih mogu prikazati linearnom funkcijom? Prikažite grafički ovisnost potrošnje o broju minuta razgovora. Analizirajte isplativost pojedine tarife ovisno o svojim navikama (više/manje minuta razgovora, više/manje SMS-poruka, više/manje mobilnih podataka...).
Istražite vezu između koeficijenata smjera međusobno okomitih pravaca.
Mijenjajte položaj pravaca micanjem istaknutih točaka i pratite zapis njihovih jednadžbi. Što zaključujete?
Provjerite svoj zaključak rješavajući sljedeći zadatak.
Pravac koji je okomit na pravac zadan jednadžbom ima koeficijent smjera:
Koeficijenti smjera međusobno okomitih pravaca su brojevi.
Predlažemo da pokušate riješiti sljedeće zadatke s Državne mature:
Proučavanjem linearne funkcije i njezina grafa zakoračili ste u svijet analitičke geometrije. Vjerujemo i nadamo se da ćete se u njemu dobro snaći jer ste dobro upoznali i usvojili osnovne pojmove koji će vas pratiti pri upoznavanju nekih drugih funkcija. Sretno!
Pred vama je igra nalik na Escape room. Tragovi postoje, ali nisu lako uočljivi. Kako biste spasili Zemlju morate pažljivo čitati upute, točno riješiti zadatke i dobro uočavati ponuđene detalje u interakciji. Sretno!
Mala pomoć: obratite pažnju na pokazivač miša - ruka znači da ste na tragu rješenja problema.