

Da bismo pomiješali vodu i sirup u omjeru
naprema
u čašu moramo uliti deset puta manje sirupa nego vode, tj. jednu desetinu količine vode. U petom razredu ste učili da se jedna desetina može zapisati u obliku dijeljenja
pa tako i izraz
naprema
zapisujemo u obliku dijeljenja
Kada govorimo o tome koliko je puta neka veličina manja od druge veličine ili koliko je puta neka veličina veća od druge, govorimo o njihovu omjeru.
Kvocijent dviju mjera ili veličina
i
nazivamo omjer tih veličina. Omjer veličina
i
pišemo u obliku
Izraz
čitamo
naprema
.
Primjer 1.
Košarkaški klub iz Vukovara u jednoj je utakmici postigao koša, a primio koševa. Koliki je omjer postignutih i primljenih koševa, a koliki je omjer primljenih i postignutih koševa?
Kada neke veličine stavljamo u omjer, moramo paziti na redoslijed veličina, tako je omjer postignutih i primljenih koševa
a omjer primljenih i postignutih koševa na toj utakmici
U omjer možemo stavljati istovrsne veličine. Možemo računati omjere duljina, površina, obujma, mase, godina, brzine, brojeva. Primjerice, godišnja stopa nataliteta jest broj rođenih stanovnika naprema ukupnog broja stanovnika u jednoj godini. Maseni udio omjer je mase određene tvari i ukupne mase svih tvari u nekoj smjesi. Pri pisanju omjera moramo paziti da mjerne jedinice istovrsnih veličina budu jednake.
Na ispitu znanja iz matematike u jednom sedmom razredu
učenika ocijenjeno je ocjenom odličan,
učenika ocijenjeno je ocjenom vrlo dobar,
učenika ocjenom dobar,
učenika ocjenom dovoljan i jedan učenik ocijenjen je ocjenom nedovoljan.
Omjer broja učenika s ocjenom nedovoljan i ukupnog broja svih učenika tog razreda koji su pisali ispit znanja jest
U posudu ulijemo četiri litre boje za zidove i litara vode. U kojem su omjeru pomiješane boja i voda?
U omjer možemo stavljati i raznovrsne veličine. Primjerice, omjer prijeđenih kilometara i vremena potrebnog za taj put zove se brzina i piše se
što čitamo kilometar na sat. Omjer mase i obujma zovemo gustoća neke tvari, pišemo
a čitamo kilogram po kubnom metru.
Kada kupujemo neki proizvod, zanima nas kolika je cijena po kilogramu ili po komadu. Omjer cijene i količine nekog proizvoda pišemo u obliku i čitamo kuna po kilogramu, ili što čitamo kuna po komadu.
Kada u omjer stavljamo raznovrsne veličine, moramo pisati mjerne jedinice.
Primjer 2.
Izračunajmo brzinu automobila ako je put od prešao za sata.
Kako se brzina mjeri u
ona je zapravo omjer prijeđenih kilometara u jednom satu. Vidimo da je
Ako automobilu treba sata da prijeđe put od kojom brzinom vozi?
Izračunajte gustoću maslinova ulja ako je masa ulja a obujam Rješenje zaokružite na dvije decimale.
Izračunajte gustoću kockice leda mase grama i obujma u i preračunajte rješenje u Odaberite obje vrijednosti.
Pomoć:
Preračunajte u i u podijelite i rezultat pomnožite s
Primjer 3.
Ako u posudu ulijemo litara vode i litre boje, omjer količine vode i boje iznosi Izračunajmo koliko je puta u posudi više vode nego boje.
Podijelimo s i dobijemo količnik U posudi ima puta više vode nego boje.
Taj količnik zove se vrijednost omjera
U omjeru broj je prvi član omjera, broj je drugi član omjera, a broj je vrijednost omjera.
Omjer dvaju brojeva jednak je količniku tih dvaju brojeva.
Drugi član omjera ne smije biti jednak nuli jer se s nulom ne može dijeliti.
Zlatni rez, zlatni omjer ili božanski omjer zasigurno je jedan od najpoznatijih omjera. Predstavlja odnos u kojem se manji dio odnosi prema većem kao veći prema cjelini. Približna vrijednost tog omjera jest a točna vrijednost dobije se konstrukcijom dužine iracionalne duljine, o čemu ćete više učiti u osmom razredu i na satovima likovne kulture. Možemo ga naći gotovo na svakom dijelu ljudskog tijela i gotovo svuda u prirodi. Primjerice, omjer glave prema duljini tijela ili omjer zadnjeg zgloba prsta i cijelog prsta predstavlja zlatni omjer. Savršeno lijepim licem smatramo lice kojem su određeni dijelovi u skladu sa zlatnim omjerom. Javlja se kod biljaka (građa češera ili cvijet ruže) i kod životinja (spirala kućice puža Nautilus ili indijske lađice). Još od antike pojavljuje se u umjetnosti, a predstavlja omjer najugodniji ljudskom oku. Koristi se u arhitekturi, slikarstvu, glazbi, dizajnu, matematici, tehnici, astronomiji i mnogim drugim područjima.
Proučite zlatni omjer, istražite gdje se nalazi oko vas i napravite radionicu o zlatnom rezu.
Ako je omjer kuna i eura takav da se dobije
za
eura, kolika je vrijednost tog omjera?
Odredite vrijednost omjera
Primjer 4.
Izračunajmo prvi član omjera
Prvi član omjera dobijemo tako da pomnožimo drugi član omjera s vrijednosti omjera:
Prema tome prvi član omjera jest
Primjer 5.
Koliki je drugi član omjera
Drugi član omjera dobijemo tako da podijelimo prvi član omjera s vrijednosti omjera:
Drugi član omjera jest
Odredite nepoznate članove omjera.
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Vrijednost omjera dobijemo tako da podijelimo prvi član s drugim.
Prvi član omjera dobijemo tako da pomnožimo vrijednost omjera s drugim članom.
Drugi član omjera dobijemo tako da podijelimo prvi član omjera s vrijednosti omjera.
Izračunajte vrijednost omjera
Vrijednost omjera iznosi
Baka je mrkve platila Kolika je cijena mrkve?
Cijena jednog kilograma mrkve iznosi
Izračunajte gustoću komada plastike ako je njegova masa
a obujam
Gustoća plastike iznosi
Izračunajte nepoznati član sljedećih omjera:
Primjer 6.
Na pakiranju omekšivača za rublje piše da ga trebamo razrijediti u omjeru To znači da na šalicu omekšivača trebamo dodati šalice vode. Koliko vode treba dodati ako stavimo šalice omekšivača?
Količinu omekšivača za rublje uvećali smo puta pa količinu vode također moramo uvećati tri puta. Znači, dodat ćemo šalica vode. Pri tome se vrijednost omjera nije promijenila: i
Vrijednost omjera neće se promijeniti ako oba člana pomnožimo ili podijelimo istim brojem, različitim od nule. Ovo nam svojstvo omjera pomaže da omjere možemo zapisati u jednostavnijem obliku.
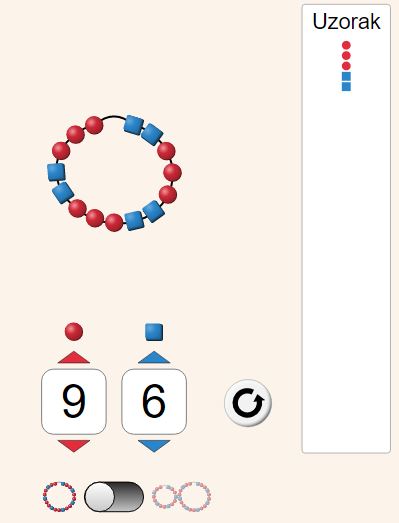
Istražite još malo omjere. Uočite da se u stupcu pojavljuje pojednostavnjeni omjer u obliku uzorka, određene nijanse boje ili jedinične cijene. Pokušajte dobiti određenu nijansu boje, uzorak ili cijenu.
PhET "Igralište proporcija" može se preuzeti na ovoj poveznici.

Slitina ili legura smjesa je nekih metala. Neke od poznatih slitina jesu čelik, bronca, bijelo zlato i mjed. Mjed je slitina cinka, bakra i još nekih metala, u raznim omjerima. Postoje razne vrste mjedi, najpoznatija je zlatna mjed. Koristi se za izradu nakita, kovanica, čahura metaka, zupčanika satova, dijelova strojeva, dijelova muzičkih instrumenata, raznih cijevi i još mnogočega. Korisno je znati da na mjedenim kvakama nema bakterija. Više o slitinama, metalima i mjedi učit ćete iz kemije, a infomacije o mjedi možete naći i na stranicama Hrvatske enciklopedije.
Kada otvorite stranicu, upišite riječ mjed. Istražite gdje su ljevaonice mjedi u Hrvatskoj te koliko ih ima.
Zlatna mjed je slitina u kojoj su cink i bakar pomiješani u omjeru
Ako imamo
cinka, trebamo dodati
bakra želimo li dobiti slitinu jednake kvalitete.
Pomoć:
Ako smo količinu cinka povećali
puta, onda moramo i količinu bakra povećati
puta želimo li sačuvati istu kvalitetu mjedi.
Primjer 7.
U oporuci piše da dva rođaka dijele nasljedstvo u omjeru
Mnogo će lakše podijeliti svoje nasljedstvo ako pojednostavne taj omjer. Pogledajmo kako će to učiniti.
Vrijednost omjera neće se promijeniti ako oba člana pomnožimo ili podijelimo istim brojem. Ovdje ćemo pomnožiti oba člana najmanjim zajedničkim nazivnikom:
Zatim uočimo da možemo oba člana podijeliti istim djeliteljem:
Rođaci će podijeliti nasljedstvo u omjeru Takav zapis mnogo je jednostavniji od onog s razlomcima, a postupak se zove pojednostavnjivanje omjera.
Omjer pojednostavnjujemo tako da ga svodimo na omjer dvaju relativno prostih brojeva.
Prisjetimo se: Relativno prosti brojevi su brojevi koji nemaju zajedničkog djelitelja većeg od
Jednostavne omjere od dvaju članova možemo pojednostavniti i običnim dijeljenjem razlomaka, ali složenije omjere od više članova uvijek pojednostavnjujemo tako da članove podijelimo zajedničkim djeliteljem.
Kada pojednostavnite omjer , dobijete
Pomoć:
Oba člana omjera pomnožite s
i podijelite s
Koje je od ponuđenih rješenja pojednostavnjen omjer
Pomoć:
Pomnožite sa zajedničkim nazivnikom
i podijelite sa zajedničkim djeliteljem
Primjer 8.
Geografska je karta nacrtana u mjerilu Ako je stvarna udaljenost između dvaju mjesta kolika je udaljenost između njihovih oznaka na karti?
Karta je nacrtana u mjerilu (omjeru) . To znači da na karti označava u prirodi, odnosno da je udaljenost između dvaju gradova u stvarnosti puta veća od udaljenosti između oznaka tih gradova na karti.
Prisjetimo se još kako je
Najprije pretvaramo kilometre u centimetre, kako bi nam bilo lakše dijeliti.
Oznake gradova na karti udaljene su .
Karta svijeta napravljena je u omjeru Zračna udaljenost između Zagreba i New Yorka iznosi oko Udaljenost između njihovih oznaka na karti bit će približno
Pomoć:
Podijelite s
Pomoć:
Odgovor upišite u obliku cijelog broja na za to predviđeno mjesto.

Karta je napravljena u mjerilu Obitelj Jukić iz Splita ide na putovanje i gleda na karti koliko su gradovi koje će posjetiti udaljeni od Splita. S obzirom na to da mjere ravnalom, dobit će zračne udaljenosti između gradova. Izmjerili su udaljenosti na karti približno ovako: Savona (Italija) Marseille (Francuska) Barcelona (Španjolska) Valencia (Španjolska) Cagliari (Italija) Rim (Italija) Izračunajte približne stvarne udaljenosti između navedenih gradova od Splita.
|
Barcelona
|
|
|
Cagliari
|
|
|
Rim
|
|
|
Marseille
|
|
|
Savona
|
|
|
Valencia
|
Pomoć:
Proširite omjer tako da pomnožite s duljinom u
Centimetre preračunajte u kilometre.
Postupak:
Primjerice za Savonu:
Istražite udaljenosti između svog mjesta i nekog grada u koji želite otputovati. Točne udaljenosti između gradova možete vidjeti na mrežnoj stranici Udaljenosti.
Primjer 9.
U oporuci piše da dva rođaka dijele nasljedstvo koje iznosi u omjeru Koliko će novca dobiti svaki rođak?
Rođaci dijele svotu od u omjeru . Da bi to pravedno podijelili, trebaju odrediti neki broj, koji se može označiti slovom koji će odrediti na koliko jednakih dijelova će se podijeliti ukupna svota novca. Taj se broj naziva koeficijent. Jedan će rođak dobiti takva dijela, a drugi takva dijela. Matematički to zapisujemo ovako:
Dobili smo linearnu jednadžbu s jednom nepoznanicom koju znamo riješiti. Dalje rješavamo:
Prvi će rođak dobiti , a drugi
Pomoć:
Pojednostavnite omjer
u
Iz jednadžbe
dobije se
Upišite rezultat u brojčanom obliku na za to predviđeno mjesto.
Omjer bijele boje prema crnoj za određenu nijansu sive boje jest Trebate li te nijanse sive boje, koliko ćete staviti bijele boje, a koliko crne u tu mješavinu?
Pomoć:
Izračunajte vrijednost omjera
Vrijednost omjera jest
Izračunajte nepoznati član omjera
Izračunajte nepoznati član omjera
Pojednostavnite omjer
Pojednostavnite omjer
Broj
rastavite na dva pribrojnika koji su u omjeru
pribrojnici su i
Izračunajte omjer učenika i učenica u svom razredu te ga pojednostavnite (ako je moguće).
Izračunajte omjer učenica i ukupnog broja učenika svog razreda te ga pojednostavnite (ako je moguće).
Često se u životu koristimo omjerima s više od dvaju članova. Takvi omjeri zovu se produženi omjeri. Primjerice, ako je u oporuci više rođaka koji dijele nasljedstvo, omjer ima više članova. Ručak pripremamo s više od dvaju sastojaka. U slitinama često imamo više od dvaju metala. Želimo li dobiti određenu nijansu boje, miješamo više boja. Pokušajte i sami naći još primjera.
Zadaci se rješavaju na isti način kao i oni s omjerima od dvaju članova.
Produženi omjer jest omjer koji ima više od dvaju članova.
Primjer 10.
U kolač se stavljaju brašno, šećer i maslac u omjeru Koliko treba dodati šećera i maslaca ako imamo brašna?
Za beton se miješaju cement, pijesak i voda u omjeru Koliko će trebati dodati pijeska i vode, ako ima cementa?
Svega treba
puta više. Pijeska
a vode
litara.
Primjer 11.
Kutovi trokuta odnose se kao Izračunajmo veličine tih kutova trokuta.
Zbroj kutova u trokutu jest Odredimo koeficijent kojim ćemo proširiti brojeve i iz zadanog omjera. Postavimo jednadžbu:
Riješimo tu jednadžbu.
Pomnožimo redom brojeve iz omjera s
pa su kutovi trokuta:
i
Petorica radnika dijele zaradu od
u omjeru
Koliko će dobiti svaki radnik?
Prvi i drugi radnik dobit će
treći će dobiti
četvrti
a peti
Rođaci dijele nasljedstvo u omjeru
Pojednostavnite taj omjer.
Pomnožite svaki član s najmanjim zajedničkim nazivnikom Pojednostavnjeni omjer iznosi
Nordijsko zlato je slitina bakra, aluminija, cinka i kositra u omjeru Koristi se za izradu europskih kovanica od i centi. Ako imate grama cinka, koliko trebate bakra, aluminija i kositra za izradu tih kovanica?
Svega treba puta više. Bakra treba aluminija a kositra
Znanje o omjerima potrebno nam je u svakodnevnom životu. U kuhanju je važno upotrijebiti dobar omjer namirnica kako bi nam jelo bilo ukusno. Želimo li nekamo putovati i snaći se na karti, moramo znati u kojem je omjeru napravljena ta karta. Želimo li obojiti zidove točno određenom nijansom, boje moramo pomiješati u određenom omjeru. Peremo li rublje, u određenom omjeru stavljamo prašak ili omekšivač. U graditeljstvu trebamo u određenom omjeru pomiješati cement, pijesak i vodu kako bismo dobili beton.
Umjetnina izrađena u omjeru zlatnog reza ugodna je ljudskom oku. Nasljedstvo i zarada od nekog posla dijele se u određenim omjerima. Omjeri se koriste u proizvodnji lijekova i kovina. Ekrani televizora i monitora izrađuju se u određenim omjerima. U matematici se omjeri koriste i u aritmetici i u geometriji. Omjeri nam trebaju i u astronomiji, fizici, kemiji i drugim znanostima.
Organizirajte se u timove i neka svaki tim istraži određeno područje u kojem se koriste omjeri te načine na koje se omjeri u tom području koriste.
Riješite zadatke kako biste procijenili svoje znanje, a ako niste sigurni kako se rješavaju, ponovno pročitajte ovu jedinicu. Nakon što sve dobro riješite, možete se nagraditi i igranjem neke od sljedećih igara u kojima se koriste omjeri:
U razredu je
učenika, od kojih je
na kraju godine imalo odličan uspjeh. Stavite u omjer broj odličnih učenika s ukupnim brojem učenika u tom razredu.
Ako automobil prijeđe put od za sata, kojom brzinom vozi?
Pojednostavnite omjere.
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Omjer pojednostavljujemo tako da oba člana pomnožimo ili podijelimo istim brojem
Pomoć:
Odgovor upišite u brojčanom obliku na za to predviđeno mjesto.
Postupak: