Matematika 7 - 10.8 Primjena linearne funkcije u svakodnevnom životu

Prisjetimo se što smo prethodno naučili!

Linearna funkcija je funkcija zadana formulom . Brojeve

$a$ i

$b$ nazivamo linearne funkcije.

$x$ nazivamo argument, a

$y$ funkcije.

null

Graf linearne funkcije je .

$x$ je nezavisna, a

$y$ zavisna .

null

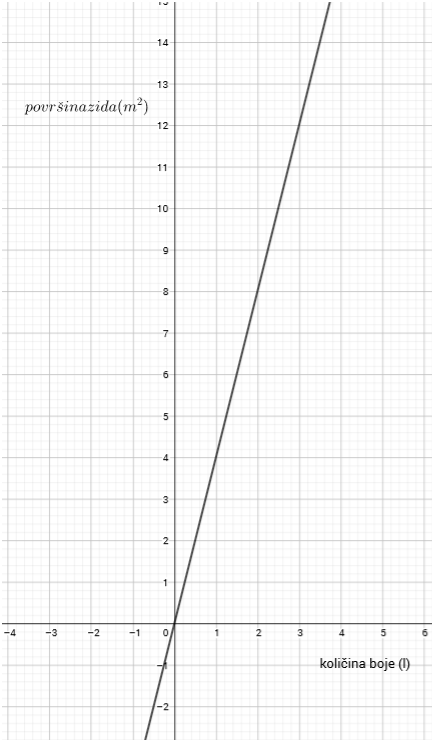
S jednom litrom boje možemo obojiti $4 m^{2} .$ Na slici je prikazan graf funkcije proporcionalnosti, tj. ovisnost količine boje i površine (zida) koju možemo obojiti.

Proučite graf sa slike i pomoću njega spojite odgovarajuće parove.

S tri litre boje možemo obojiti	$12 m^{2}$
S dvije litre boje možemo obojiti	$4 m^{2}$
S jednom litrom boje možemo obojiti	$8 m^{2}$

Pomoć:

$y = 4 x$

null

Primjer 1.

Račun za vodu naplaćuje se $0.35 kn$ po potrošenom $m^{3}$ vode, a stalna naknada iznosi $45 kn .$

Napišimo funkciju ovisnosti veličine računa i potrošnje vode.

Izračunajmo koliko će iznositi račun ako je potrošeno $23 m^{3}$ vode.

Izračunajmo koliko je potrošeno vode ako je račun iznosio $59 kn$ i $70$ lipa.

Označimo s $x$ količinu potrošene vode izražene u $m^{3},$ a s $y$ iznos računa.

Nakon potrošenih $x$ $m^{3}$ vode platit ćemo $0.35 \cdot x kn .$ Budući da se obračunava stalna naknada od $45 kn,$ račun za potrošnju vode obračunavat će se po formuli $y = 0.35 \cdot x + 45 .$
Uvrštavanjem $x = 23$ u formulu linearne funkcije dobit ćemo $y = 0.35 \cdot 23 + 45 = 8.05 + 45 = 53.05 .$

To znači da će račun iznositi $53$ kune i $5$ lipa.
Uvrštavanjem $y = 59.70$ u formulu linearne funkcije dobit ćemo

$0.35 x + 45 = 59.70$

$0.35 x = 59.70 - 45$

$0.35 x = 14.7 / : 0.35$

$x = 42 .$

To znači da je potrošeno $42 m^{3}$ vode.

Kolekcija zadataka 1

Zadatak 1.

Ivan je za rođendan dobio $300 kn$ što mu nije dovoljno da kupi novi mobitel. Zato je odlučio uštedjeti $75 kn$ mjesečno. U bilježnici

iskažite ovisnost sume novca o broju mjeseci koje štedi.
izračunajte koliko će novaca imati za šest mjeseci.
izračunajte koliko će dugo morati štedjeti ako mu je za kupnju mobitela potrebno $1 200 kn .$

$x . . .$ broj mjeseci štednje

$y . . .$ količina novca

$y = 75 x + 300$
$x = 6$

$y = 75 \cdot 6 + 300$

$y = 450 + 300 = 750$

Nakom šest mjeseci uštedjet će $750 kn .$
$y = 1 200$

$75 \cdot x + 300 = 1 200$

$75 \cdot x = 1 200 - 300$

$75 \cdot x = 900 / : 75$

$x = 12$

Potrebno je štedjeti $12$ mjeseci.

Zadatak 2.

Agencija iznajmljuje automobile uz naknadu od $400 kn$ i $200 kn$ po danu. Formula ovisnosti iznosa računa o broju iznajmljenih automobila glasi:

$y = 400 x + 200$

$y = 200 x + 400$

$y = 200 x + 200$

$y = 400 x + 400$

null

Zadatak 3.

Služba taksija naplaćuje $27 kn$ za polazak taksija i $8 kn$ po svakom prijeđenom kilometru. Služba taksija naplatit će vožnju po formuli $y = 27 x + 8 .$

null

Postupak:

$y = 8 x + 27$

Zadatak 4.

Majstor Štef svoj dolazak naplaćuje

$80 kn .$ Svaki dodatni sat rada naplaćuje

$100 kn .$ Linearna funkcija koja opisuje ovisnost novca o broju radnih sati je . Ako je majstor Štef radio tri sata, tada je naplatio kuna.

Pomoć:

$x = 3$

Postupak:

$y = 100 \cdot 3 + 80 = 380$

Zatvori

Kolekcija zadataka 2

Zadatak 5.

Automobil se kreće prosječnom brzinom od $75 km/h .$ Koliko mu je potrebno vremena da iz Zagreba dođe u Slatinu ako je udaljenost između tih dvaju gradova $180 km ?$

$2$ sata i

$40$ minuta

$2$ sata i

$30$ minuta

$2$ sata i

$24$ minute

Pomoć:

$x ...$ vrijeme

$y ...$ . duljina puta

$y = 75 \cdot x$

Postupak:

$y = 180$

$75 \cdot x = 180 / : 75$

$x = 2.4$ sata

$x = 2$ sata i $24$ minute

Zadatak 6.

Mjesečna pretplata za telefon iznosi

$45 kn .$ Cijena razgovora po minuti iznosi

$0.15 kn .$ Formula ovisnosti iznosa telefonskog računa o broju minuta razgovora glasi .
Ako je potrošeno

$250$ minuta, tada će mjesečni račun iznositi kuna.
Ako je mjesečni račun iznosio

$53 kn$ i

$40$ lipa, taj je mjesec razgovarano minuta.

null

Zadatak 7.

Kilogram krušaka stoji

$12 kn .$ Formula ovisnosti iznosa računa o količini kupljenih krušaka glasi .
Ako kupimo

$3.5 kg$ krušaka, račun će iznositi kune. Za

$kg$ platit ćemo

$37.50 kn .$

null

Zatvori

Zadatak 8.

S grafa očitajte:

Koliko se kilometara može prijeći s

$20$ litara benzina.

Koliko je litara benzina potrebno da bi se prešlo

$550$ kilometara.

S $20$ litara benzina može se prijeći $250$ kilometara.
Da bi se prešlo $550$ kilometara, potrebne su $44$ litre benzina.

10.8 Primjena linearne funkcije u svakodnevnom životu

Na početku...

Prisjetimo se što smo prethodno naučili!

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zadatak 3.

Zadatak 4.

Kolekcija zadataka 2

Zadatak 5.

Zadatak 6.

Zadatak 7.

Ponovimo!

Zadatak 8.

...i na kraju