

Znate li kako će majstori iz animacije izračunati površinu cerade kojom žele prekriti bazen?
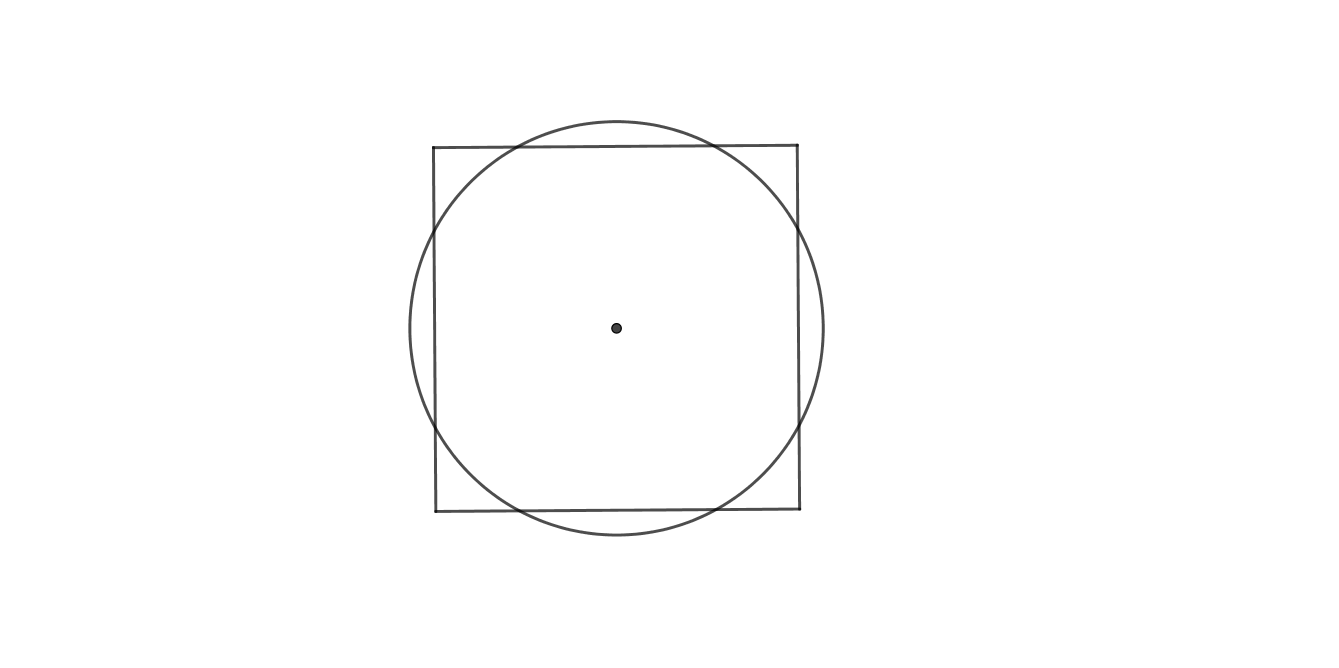
Kvadratura kruga je jedan od najstarijih nerješivih matematičkih problema. Problem je poznat još od antičkih vremena. Izraz kvadratura kruga danas se upotrebljava u svakodnevnom životu kao izraz za neki nerješiv problem.
Ako je zadan krug polumjera
postavlja se pitanje može li se konstruirati samo ravnalom i šestarom kvadrat iste površine kao i zadani krug. Taj je problem pokušavalo riješiti mnogo matematičara, no tek je 1882. njemački matematičar Ferdinand Lindemann dokazao da je to nemoguće zbog broja
koji je beskonačan neperiodički decimalni broj i ne može se točno konstruirati dužina duljine
primjerice centimetara.
Prisjetimo se da pravilnom mnogokutu možemo opisati kružnicu. Što pravilni mnogokut ima više stranica, to se njegova površina više poklapa s površinom kružnice. Površina pravilnog mnogokuta koji bi imao beskonačno mnogo stranica bila bi jednaka površini njemu opisanog kruga. Za naše oko je dovoljno samo jako povećati broj stranica pravilnog mnogokuta. Podijelimo mnogokut na karakteristične trokute, odnosno kružnicu na odgovarajuće kružne isječke.
U GeoGebrinoj simulaciji možete vidjeti što se događa kad povećate broj stranica pravilnog mnogokuta
Odaberite što veći
tako da se promatrani mnogokut naoko preklopi s kružnicom.
Promotrite ljubičastu i narančastu polovicu. Kad pomičemo klizač "presložite krug", vidimo da se obje polovice mnogokuta rastvore i spoje u paralelogram.
S obzirom na to da je mnogokut površinom naoko preklopio krug, možemo zamisliti da su površine mnogokuta i kruga jednake ili toliko približno jednake da je razlika zanemariva. Paralelogram koji smo dobili razlaganjem mnogokuta tada ima istu površinu kao mnogokut, a možemo reći i gotovo istu kao krug.
Pogledajmo stranicu i visinu paralelograma. Visina je približno jednaka duljini polumjera a stranica je približno jednaka duljini polukružnice, odnosno polovini opsega kruga
Površinu paralelograma dobijemo kad pomnožimo duljine tih dviju dužina,
a kako je površina paralelograma za mnogokut s beskonačno mnogo stranica jednaka površini opisanog kruga, dobivamo formulu za površinu kruga.
Površina kruga računa se prema formuli odnosno
Primjer 1.
Izračunajmo površinu kruga polumjera
Uvrstimo u formulu Kao i kod opsega kruga, ako želimo točno rješenje, ostavimo a ako želimo približno rješenje, uvrstimo
Tako iz formule
dobijemo
ili
Izračunajte točno i približno površinu kruga promjera
Pomoć:
Postupak:

Pomoć:
Primjer 2.
Izračunajmo promjer kruga površine
Iz formule za površinu kruga izračunamo duljinu polumjera kruga:
Ako je polumjer kruga promjer kruga je
Izračunajte opseg kruga čija površina iznosi približno .

Pomoć:
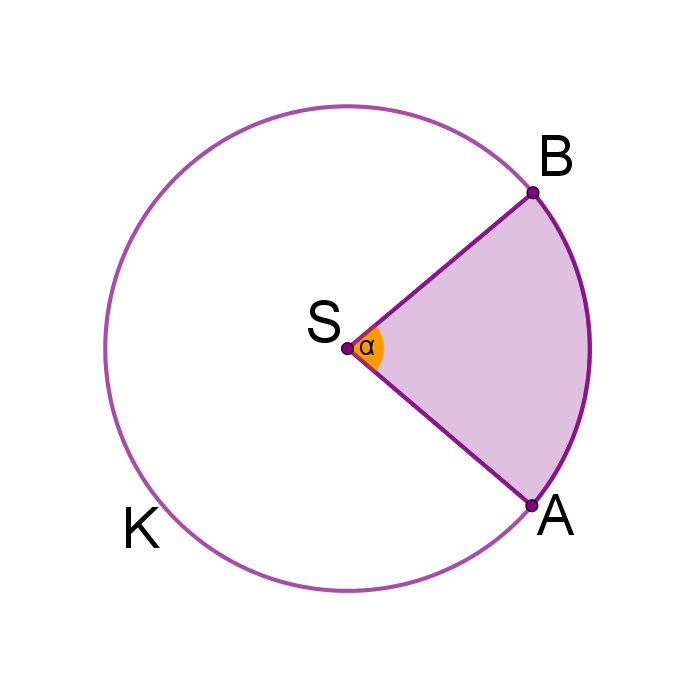
Kružni isječak je dio kruga. S obzirom na to da krugu možemo računati površinu, pogledajmo kako ćemo računati površinu kružnom isječku.
Uobičajena oznaka za površinu kružnog isječka je
Na slikama su krugovi istog polumjera. Sa slika vidimo da za veći središnji kut dobijemo kružni isječak površine.
Pomoć:
Dobro pogledajte slike. Veća ljubičasta ploha znači i veću površinu kružnog isječka.
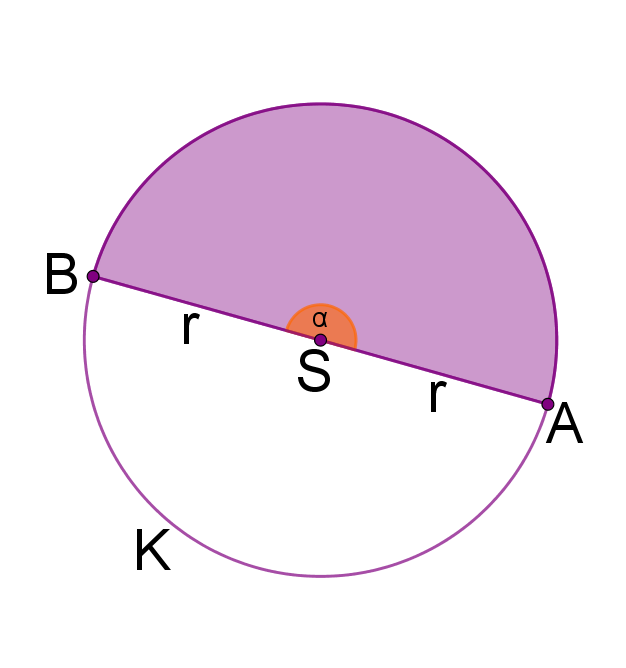
Pomoć:
Površina polukruga je površine kruga, u ovom slučaju .
Pomoć:
Ispruženi kut od je punog kuta od
Pomoć:
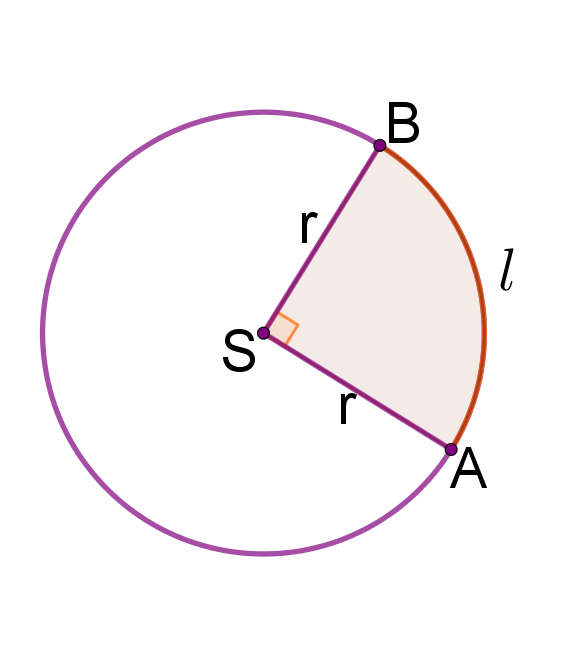
Središnji kut na slici je kut veličine .
Pomoć:
Pažljivo pogledajte sliku.
Središnji kut od je četvrtina punog kuta od
Površina kružnog isječka sa slike je površine kruga.
Pomoć:
Ako središnji kut podijelimo na
jednaka dijela, i krug je podijeljen na
jednaka dijela.
Cijelom krugu pripada središnji kut od Spojite parove dijelova kruga i pripadnog središnjeg kuta.
|
trećina kruga
|
središnji kut |
|
dvadesetina kruga
|
središnji kut |
|
devetina kruga
|
središnji kut |
|
desetina kruga
|
središnji kut
|
Pomoć:
Nacrtajte krug bilo kojeg polumjera. Puni kut iznosi
Podijelite puni kut s
i
i nacrtajte kutomjerom središnji kut.
Promjer kruga je Izračunajte površinu kruga.
Pomoć:
Nacrtajte četiri kruga promjera i podijelite ih na kružne isječke koji se pojavljuju u lijevom stupcu zadatka. Spojite parove dijela kruga i površine pripadnog dijela kruga (kružnog isječka).
|
četvrtina kruga
|
|
|
petina kruga
|
|
|
šestina kruga
|
|
|
dvanaestina kruga
|
Pomoć:
Podijelite krug na
ili
dijelova. Zatim podijelite površinu kruga s
ili
Pogledajte još jedanput prethodna četiri zadatka i razmislite o promjenama veličine središnjeg kuta i površine pripadnog kružnog isječka. Što možete zaključiti?
Koliko se puta povećala veličina središnjeg kuta, toliko se puta površina kružnog isječka istog kruga. Koliko se puta smanjila veličina središnjeg kuta, toliko se puta površina kružnog isječka istog kruga.
Pomoć:
Dobro pogledajte prethodne zadatke i promotrite veličine središnjih kutova i površine pripadnih kružnih isječaka.
Površina kružnog isječka i veličina pripadnog središnjeg kuta istog kruga međusobno su veličine.
Pomoć:
Ako za dvije veličine vrijedi: koliko puta se poveća ili smanji jedna veličina, toliko će se puta povećati ili smanjiti i druga veličina, za te dvije veličine kažemo da su proporcionalne veličine.
Površina kružnog isječka i veličina pripadnog središnjeg kuta istog kruga međusobno su proporcionalne veličine pa vrijedi razmjer:
površina kružnog isječka : površina cijelog kruga = veličina pripadnog središnjeg kuta : veličina punog kuta
Riješimo razmjer
i dobijemo formulu za površinu kružnog isječka
odnosno
Površina kružnog isječka koji pripada krugu polumjera i koji ima središnji kut računa se prema formuli
Primjer 3.
Polumjer kruga je Izračunajmo površinu kružnog isječka koji pripada tom krugu i ima središnji kut veličine
Površinu kružnog isječka računamo prema formuli
odnosno
Uvrstimo podatke u formulu
Izračunajte površinu kružnog isječka koji pripada krugu polumjera
i ima središnji kut
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Uvrstite duljinu polumjera i veličinu kuta u formulu za površinu kružnog isječka, skratite razlomak i pomnožite preostale brojeve ili zadatak riješite logički s pomoću dijelova punog kuta i proporcionalnog dijela površine kruga.
Pogledajmo još malo slike kružnih isječaka. U krugu istog polumjera većem kružnom isječku pripada dulji kružni luk. Provjerimo omjere duljina kružnih lukova i omjere površina pripadnih kružnih isječaka
.
Formula za duljinu kružnog luka je
Polumjer kruga je Prepišite u bilježnicu i popunite tablicu.
| Središnji kut | Duljina kružnog luka | Površina kružnog isječka |
|---|---|---|
| Središnji kut | Duljina kružnog luka | Površina kružnog isječka |
|---|---|---|
U krugu istog polumjera za dvostruko dulji kružni luk dobijemo veću površinu pripadnog kružnog isječka.
Pomoć:
Pažljivo pogledajte tablicu. Izračunajte omjer duljina kružnih lukova i omjer površina pripadnih kružnih isječaka.
Postupak:
Polumjer kruga je
Prepišite u bilježnicu i popunite tablicu.
| Središnji kut | Duljina kružnog luka | Površina kružnog isječka |
|---|---|---|
| Središnji kut | Duljina kružnog luka | Površina kružnog isječka |
|---|---|---|
U krugu istog polumjera za trostruko kraći kružni luk dobijemo manju površinu pripadnog kružnog isječka.
Pomoć:
Pažljivo pogledajte tablicu. Izračunajte omjer duljina kružnih lukova i omjer površina pripadnih kružnih isječaka.
Postupak:
Pogledajte još jedanput prethodne zadatke i razmislite o promjenama duljine kružnog luka i površine pripadnog kružnog isječka. Što možete zaključiti?
Koliko se puta povećala duljina kružnog luka, toliko se puta
površina pripadnog kružnog isječka istog kruga. Koliko se puta smanjila duljina kružnog luka, toliko se puta površina pripadnog kružnog isječka istog kruga.
Pomoć:
Dobro pogledajte prethodne zadatke i promotrite duljine kružnih lukova i površine pripadnih kružnih isječaka.
Duljina kružnog luka i površina pripadnog kružnog isječka istog kruga međusobno su veličine.
Pomoć:
Ako za dvije veličine vrijedi: koliko puta se poveća ili smanji jedna veličina, toliko će se puta povećati ili smanjiti i druga veličina, za te dvije veličine kažemo da su proporcionalne veličine.
Iz navedenog slijedi da možemo površinu kružnog isječka prikazati i s pomoću duljine kružnog luka.
Promotrimo formulu za površinu kružnog isječka i formulu za duljinu kružnog luka:
i
U formuli za površinu kružnog isječka nazivnik možemo zapisati u obliku umnoška broja i :
Izdvojimo iz formule za površinu kružnog isječka dio koji pripada formuli za duljinu kružnog luka
napišimo oznaku za duljinu kružnog luka umjesto formule
i pomnožimo
Površina kružnog isječka koji pripada krugu polumjera i kojem je duljina pripadnog kružnog luka računa se prema formuli
Primjer 4.
Izračunajmo površinu kružnog isječka koji pripada krugu promjera i kojem je duljina pripadnog kružnog luka
Polumjer kruga je duljina pripadnog kružnog luka je
Uvrstimo u formulu za površinu kružnog isječka:
Površina kružnog isječka je
Izračunajte površinu kružnog isječka koji pripada krugu polumjera
a duljina pripadnog kružnog luka mu je
Pomoć:
Primjer 5.
Izračunajmo opseg kruga kojem pripada kružni isječak površine i pripadnog središnjeg kuta
Formula za opseg kruga je znači da moramo izračunati duljinu polumjera
Iz formule za površinu kružnog isječka izračunat ćemo traženu veličinu.
U uvrstimo zadane podatke:
skratimo razlomak
Opseg kruga je
Izračunajte promjer kruga kojem pripada kružni isječak površine ako je veličina središnjeg kuta toga kružnog isječka
Pomoć:
Postupak:
Primjer 6.
Izračunajmo veličinu središnjeg kuta kružnog isječka površine koji pripada krugu opsega
Iz formule za opseg kruga izračunamo duljinu polumjera:
U formulu za površinu kružnog isječka uvrstimo poznate podatke:
Središnji kut kružnog isječka je veličine
Spojite parove ako je
polumjer kruga kojem pripada kružni isječak površine
koji ima središnji kut
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Preporučujemo upotrebu džepnog računala u ovom zadatku.
Primjer 7.
Ako kružni isječak površine pripada krugu površine , izračunajte duljinu pripadnog kružnog luka.
Iz formule za površinu kruga izračunamo polumjer kruga:
Iz formule za površinu kružnog isječka izračunamo duljinu kružnog luka:
Duljina kružnog luka je
Pomoć:
Postupak:

Na slici vidimo isječak sira. Kolika je površina etikete na isječku sira ako znamo da je to šestina kruga promjera
Pomoć:

Djeca su slučajno loptom razbila staklo na jednom dijelu prozora na slici. Ako znamo da je promjer prozora
kolika je približna površina stakla koju će morati zamijeniti?
Pomoć:
Postupak:

Nacrtajte uzorak za ukrasnu mozaičnu kupaoničku pločicu kvadratnog oblika u bilježnicu u pravoj veličini i izmjerite duljinu dijagonale te pločice. Izračunajte površinu ljubičastog dijela pločice stranice duljine
Površina kvadrata je Od površine kvadrata oduzmemo površine kružnog isječka polumjera i središnjeg kuta Može se primijetiti da ta kružna isječka čine jedan krug polumjera pa je
Izmjerite duljinu dijagonale na svojem crtežu u bilježnici. Duljina dijagonale pločice je približno
Izračunajmo još i površinu kruga u sredini. Duljinu promjera toga kruga izračunamo tako da od duljine dijagonale oduzmemo polumjere kružnih isječaka,
Polumjer kruga u sredini je pa je površina toga kruga
Površina ljubičastog dijela pločice je
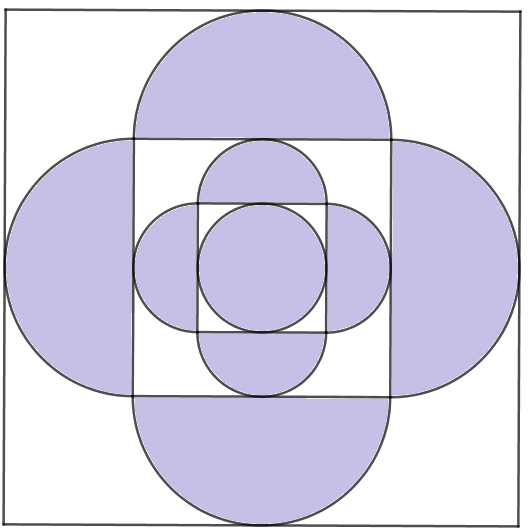
Izračunajte površinu neobojenog dijela ukrasne mozaične kupaoničke kvadratne pločice, duljine stranice
Površinu neobojenog dijela dobijemo tako da od površine kvadrata oduzmemo površine polukrugova i kruga.
Površina kvadrata je Od velikih polukrugova, kad se spoje, dobijemo dva kruga polumjera Njihova površina je
Od malih polukrugova, kad se spoje, dobijemo dva kruga polumjera Njihova površina je
Polumjer kruga u sredini je pa je njegova površina
Površina neobojenog dijela je
Po uzoru na prethodna dva zadatka, dizajnirajte sami neku kvadratnu kupaoničku pločicu s kružnim uzorcima. Izračunajte površine obojenih dijelova.
Organizirajte razrednu izložbu dizajniranih keramičkih pločica na panou.
U ovoj jedinici naučili ste kako izračunati površinu kruga i površinu kružnog isječka. Za površinu kružnog isječka možete se koristiti dvjema formulama, a možete je računati i kao dio kruga zbog proporcionalnosti površine kružnog isječka i veličine pripadnog središnjeg kuta.
Za kraj pogledajmo što je bilo s bazenom iz animacije s početka jedinice.
Pomoć:
Pomoć:
Postupak:
Treba preračunati u i to pribrojiti duljini polumjera.
Pomoć:
Pomoć:
Pomnožite površinu bazena u sa i cijenu uvećajte za