

Ako se zagledate u točku u središtu kružnica i udaljite glavu od monitora, kružnice će se početi okretati. Kad počnete približavati glavu, kružnice će se okretati u suprotnom smjeru. Pokušajte.

Optičke iluzije bojom, kontrastima i uzorcima mogu stvoriti slike koje zbunjuju mozak, stvarajući prizor koji se ne podudara sa stvarnim prikazom. Naš mozak se pokušava prilagoditi i interpretirati prizor koji vidi čineći ga smislenim te se katkad prevari gledajući ono što se ne čini stvarnim.
Nekoliko optičkih iluzija možete vidjeti ovdje, a možete posjetiti i Muzej iluzija.
Za uvježbavanje kružnice i kruga predlažemo nekoliko zadataka koje možete samostalno riješiti u bilježnicu ili u nekom interaktivnom elementu. Zadnjih nekoliko zadataka je za one koji žele znati više, ali svi ih možete pokušati riješiti. Nakon što riješite zadatke, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili zamolite da vam pomognu ako vam je neki zadatak težak.
Istražite gdje se u vašoj okolini pojavljuje krug, kružnica ili njihovi elementi. Nađite što više primjera i prikažite ih prezentacijom.

Olimpijske igre su sportsko natjecanje koje se održava svake četiri godine. Prve Igre nastale su u antičkoj Grčkoj, ali su se tijekom vremena prestale održavati. Ponovno su oživljene potkraj 19. stoljeća pod vodstvom francuskog baruna Pierrea de Coubertina.
Simbol Olimpijskih igara je pet povezanih krugova u plavoj, žutoj, crnoj, zelenoj i crvenoj boji. Coubertin je izabrao taj znak kao simbol pet naseljenih kontinenata svijeta (računajući Ameriku kao jedan kontinent). Isto tako, svaka država koja je sudjelovala na Olimpijskim igrama imala je barem jednu od boja simbola Olimpijskih igara. Kako je motiv pet krugova nastao nakon petih Olimpijskih igara, smatra se da krugovi predstavljaju pet uspješno održanih Igara. Uz to, krugovi prikazuju kontinuitet i cjelovitost te su izvrstan simbol Olimpijskih igara.
Više o Olimpijskim igrama možete pročitati ovdje.

Konstruirajte znak Olimpijskih igara kao na slici. U kojem su međusobnom položaju crna i žuta kružnica, a u kojem žuta i crvena kružnica na slici?
Organizirajte matematičke olimpijske igre u razredu. Podijelite se u skupine. Neka svaka skupina osmisli jednu disciplinu (aktivnost). Pripremite način bodovanja svih aktivnosti. Natječite se i proglasite pobjednika.
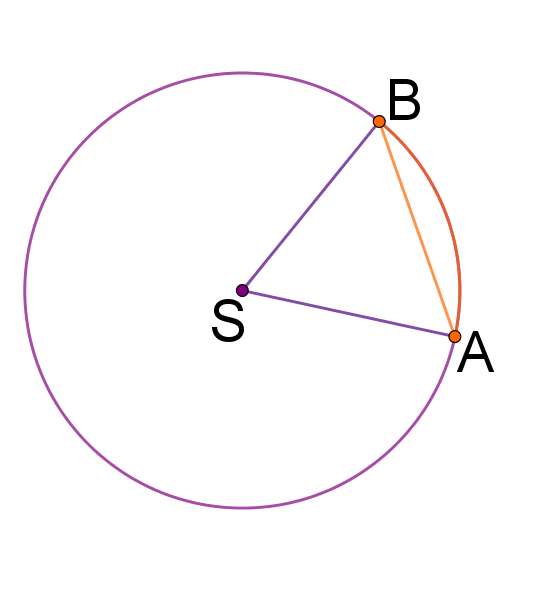
Koliki je središnji kut nosača na panoramskom vrtuljku ilustriranom na slici, ako je obodni kut prikazan na slici veličine
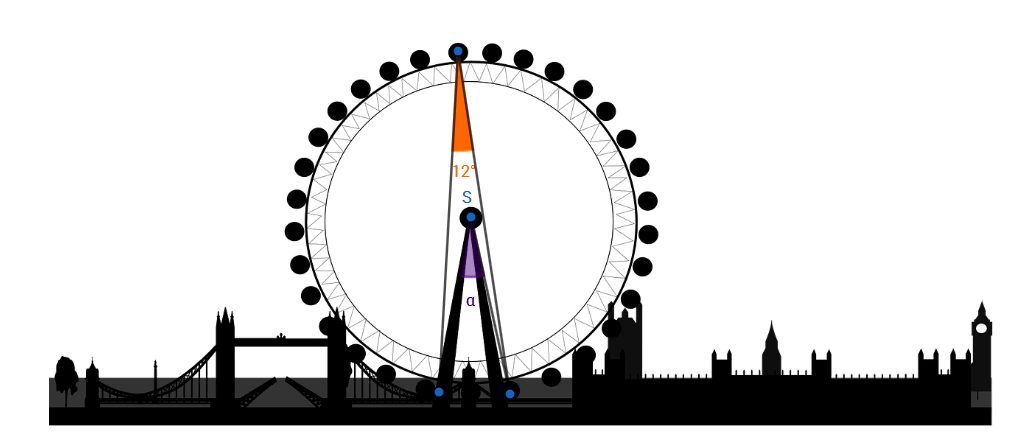
Središnji kut nosača i dani obodni kut nad istim su kružnim lukom. Znamo i da je središnji kut dvostruko veći od obodnog kuta nad istim kružnim lukom. Prema tome, središnji kut je
Izradite maketu Ferrisova kotača Adria Eye, najvećeg panoramskog vrtuljka u Hrvatskoj, koji se nalazi u Biogradu na Moru, i osmislite nekoliko zadataka vezanih uz njegove mjere.
Konstruirajte kružnicu promjera i na njoj označite tri točke i Točkama i povucite sekantu, a točkom tangentu na tu kružnicu.
Konstruirajte pravokutni trokut
s hipotenuzom
duljine
i duljinom katete
Popunite tablicu; je duljina polumjera kruga, veličina središnjeg kuta, duljina pripadnog kružnog luka, površina pripadnog kružnog isječka, opseg kruga i površina kruga te
|
|
|||||

Pomoć:
Po površini kružnog toka gradsko komunalno poduzeće želi zasaditi ruže. Promjer kružnog toka je metara. Ruže sadimo tako da oko svake bude razmak polumjera približno Koliko sadnica ruža trebaju nabaviti za taj kružni tok?
Pomoć:
Polumjer kružnog toka je
Postupak:
Površinu kružnog toka podijelite s površinom razmaka oko svake sadnice.

Vrtlar je odlučio napraviti jezerce u vrtu i u njega posaditi vodene ljiljane.
Jezerce je kružnog oblika promjera pa je njegova površina približno
Pomoć:
Pomoć:
Po površini u jezerce stane oko listova ljiljana.
Pomoć:
Najviše bi površine jezerca smjelo biti pokriveno, pa bi trebalo ukloniti oko listova.
Pomoć:
od
Postupak:
Broj listova koje treba ukloniti zaokružite na desetice.
Studentski centar sastoji se od odvojenih zgrada. Sve susjedne zgrade udaljene su Uprava Studentskog centra odlučila je staviti internetski odašiljač na mjesto s kojega bi se odaslao jednak signal prema svim zgradama. Pomozite upravi u odluci na koje će mjesto staviti odašiljač, prikazujući zgrade i odašiljač točkama u omjeru
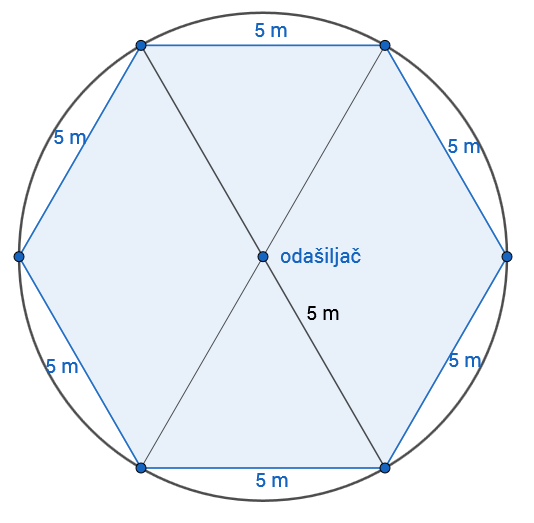
Odašiljač treba staviti u središte kružnice opisane šesterokutu čiji vrhovi predstavljaju zgrade. Polumjer kružnice je
Odaberite dvije susjedne zgrade ili kuće susjedne onoj u kojoj vi živite, ali tako da ne budu sve tri zgrade ili kuće u nizu. Odredite točku u koju biste stavili odašiljač da biste svi imali jednak internetski signal. Rješenja prikažite maketom ili plakatom.

Arheolozi su pronašli krhotinu tanjura starog tisuću godina, koja izgleda kao na slici. Pomozite im i krhotinu dopunite da bi se vidjelo kako je taj tanjur izgledao kad je bio potpun.
Primijetimo dva kružna luka na tanjuru. Izaberemo tri točke
koje leže na jednom kružnom luku. Povežemo ih u trokut. Konstruiramo simetrale dviju stranica trokuta. U točki gdje se simetrale sijeku nalazi se središte kružnica kojima pripadaju kružni lukovi tanjura. Nadocrtamo kružnice i dobili smo obrube tanjura. Možete ga ispuniti i povijesnim uzorcima.
Izradite od kartona krhotine povijesnih tanjura. Ispunite ih uzorcima. Razmijenite ih s ostalim učenicima te rekonstruirajte tanjure čije su vam konstrukcije dali. Najbolje radove nagradite i izložite.
Opsezi dviju koncentričnih kružnica su i Izračunajte površinu kružnog vijenca određenog tim kružnicama.
Rješenje pogledajte u videozapisu "Površina kružnog vijenca".
Zadaci s kružnicom i krugom često se pojavljuju na državnoj maturi pa predlažemo da pogledate i sljedeće zadatke:
Za kraj ponovite osnovne formule koje se pojavljuju kod kruga i kružnice tako da prepišete tablicu u bilježnicu i popunite je. Najprije ju riješite samostalno, a zatim usporedite svoje rješenje s ponuđenim.
Popunite tablicu;
je duljina polumjera kruga,
veličina središnjeg kuta,
duljina pripadnog kružnog luka,
površina pripadnog kružnog isječka,
opseg kruga i
površina kruga te
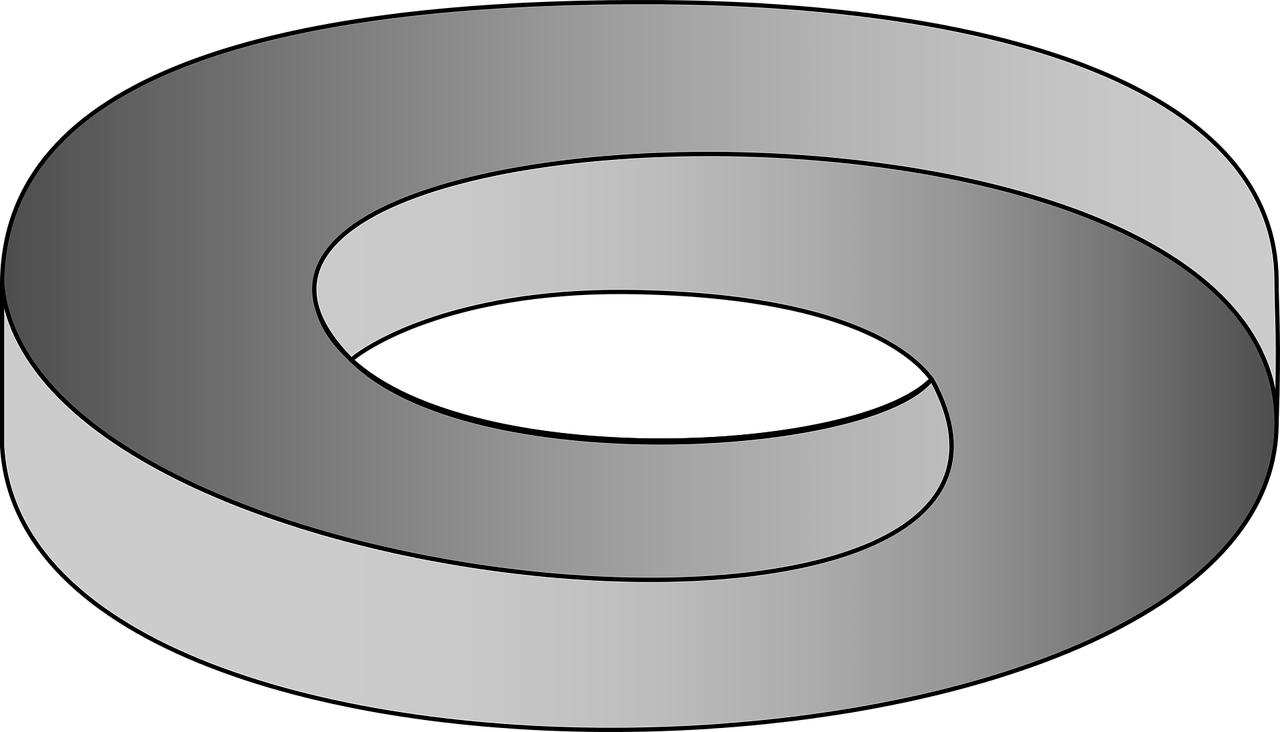
Nakon riješene tablice, pokušajte nacrtati optičku iluziju kao na slici.