

Prisjetimo se da je opseg nekog lika zbroj duljina svih stranica tog lika.
Dva su trokuta slična ako su im odgovarajući kutovi jednakih veličina i duljine odgovarajućih stranica proporcionalne.
Koeficijent sličnosti omjer je duljina odgovarajućih stranica sličnih trokuta
Duljine stranica sličnog trokuta dobijemo tako da pomnožimo duljine stranica trokuta s koeficijentom sličnosti,
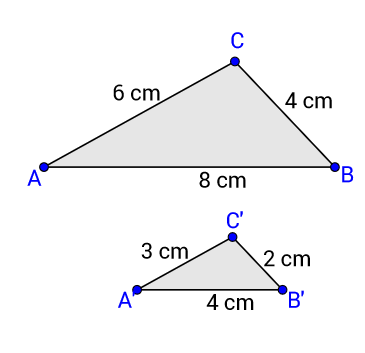
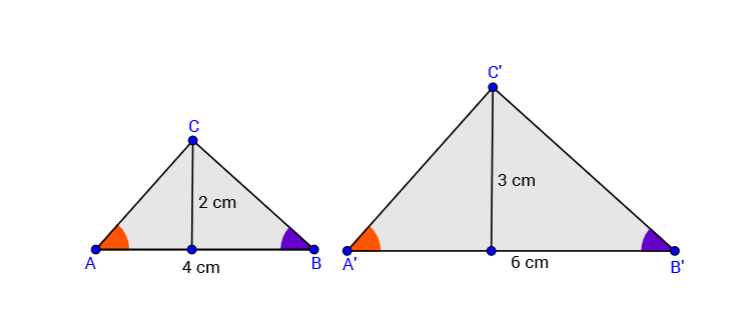
Zadani su trokuti i kao na slici.
Da bismo provjerili sličnost, stavljamo odgovarajuće duljine stranica u omjer.
Omjeri su jednaki pa su trokuti slični prema SSS poučku.
Koeficijent sličnosti trokuta je
Opseg trokuta
Opseg trokuta
Omjer ili
Što zamjećujete?
Omjer duljina odgovarajućih stranica iznosi
Omjer opsega tih dvaju trokuta također iznosi
Vrijedi li to i općenito za sve slične trokute?
Izračunajte opsege i provjerite omjere opsega sličnih trokuta s pomoću interaktivne simulacije.
U simulaciji uočite odgovarajuće kutove sličnih trokuta. Uočite omjere odgovarajućih stranica sličnih trokuta i usporedite s omjerom opsega sličnih trokuta.
Omjer opsega sličnih trokuta jednak je koeficijentu sličnosti tih trokuta.
Možemo zapisati i ovako: Ako za slične trokute i vrijedi onda je i
Primjer 1.
Trokut sličan je manjem trokutu i omjer duljina njihovih odgovarajućih stranica iznosi Ako je opseg trokuta koliki je opseg trokuta
Omjer opsega sličnih trokuta jednak je omjeru duljina odgovarajućih stranica tih trokuta. Pritom treba paziti na to koji je trokut veći, a koji manji. Veći trokut ima dulji opseg, manji trokut ima manji opseg. Trokut
je manji, a trokut
je veći pa pišemo
Uvrstimo podatke u taj razmjer i riješimo ga.
Opseg manjeg trokuta iznosi
Dva su trokuta slična s koeficijentom
Ako je opseg većeg trokuta
koliki je opseg manjeg trokuta?
Omjer opsega sličnih trokuta jednak je koeficijentu sličnosti tih trokuta. Označimo opseg manjeg trokuta s
Tada iz izraza
slijedi
Duljine odgovarajućih stranica dvaju međusobno sličnih trokuta iznose
i
Koliki je opseg većeg trokuta ako je opseg manjeg
Pomoć:
Primjer 2.
Trokuti i su slični. Duljine stranica trokuta su Opseg njemu sličnog trokuta je Izračunajmo duljine stranica trokuta
Izračunajmo opseg trokuta
Opseg njemu sličnog trokuta iznosi
Trokut
je trokut većeg opsega pa će i duljine odgovarajućih stranica biti veće.
Iz
slijedi
Iz slijedi .
Iz slijedi .
Prvo rješenje dobili smo u milimetrima jer su duljine trokuta
koje smo uvrstili u jednadžbe bile u milimetrima. U ovom primjeru rješenja ljepše izgledaju u centimetrima pa ćemo tako i zapisati.
Duljine stranica trokuta
iznose
i
Trokut
sličan je manjem trokutu
Duljine stranica manjeg trokuta iznose
i
Odredite duljine stranica većeg trokuta opsega
Dovucite oznake na odgovarajuće duljine stranica.
|
|
|
|
|
|
|
|
Pomoć:
Izračunajte opseg manjeg trokuta.
Preračunajte opseg u
Postavite pravilan omjer.
Postupak:
Opseg manjeg trokuta iznosi
Ako nekom trokutu povećamo duljine stranica puta, i njegov će se opseg povećati puta.
Pomoć:
Koliko puta povećamo duljine stranica trokuta, toliko će se puta povećati i njegov opseg.
Ako nekom trokutu umanjimo duljine stranica puta, njegov će se opseg umanjiti puta.
Pomoć:
Koliko puta umanjimo duljine stranica trokuta, toliko će se puta umanjiti i njegov opseg.
Ako nekom trokutu povećamo duljine stranica puta, i njegov će se opseg umanjiti puta.
Pomoć:
Koliko puta povećamo duljine stranica trokuta, toliko će se puta povećati i njegov opseg.

Na slici vidimo prometni znak u obliku trokuta.
Znate li na što upozorava taj prometni znak?

Promatrajmo bijeli trokut u sredini i cijeli trokut znaka. Vanjske stranice cijelog znaka promatrajte tako da produljite stranice i zaobljeni dio zamijenite vrhovima trokuta, kao na slici.
Organizirajte se u timove. Pronađite prometni znak, ovaj isti ili neki drugi u obliku trokuta. Pripazite da ne stojite na cesti nego sa strane.
Izmjerite potrebne veličine. Vanjske stranice izmjerite i nacrtajte tako da ih produljite kako biste zaobljeni dio mogli zamijeniti vrhovima trokuta kao na slici u zadatku. Nacrtajte od kartona takav prometni znak u stvarnoj veličini.
To donesite u školu i dalje radite u učionici.
Izmjerite duljine stranica cijelog znaka s produženim stranicama i bijelog trokuta. Nacrtajte i izmjerite duljine visine na jednu stranicu tih trokuta.
Izračunajte površinu znaka i površinu bijelog dijela.
Zapišite podatke uredno u tablicu.
Stavite u omjer duljine stranica trokuta.
Stavite u omjer duljine visina tih trokuta koje ste izmjerili.
Stavite u omjer površine tih trokuta.
Što zamjećujete? Jesu li omjeri jednaki?
Usporedite svoje rezultate s rezultatima ostalih timova u razredu.
Napravite plakat za razredni pano.
Prisjetimo se.
Površina lika jest broj kvadratnih jedinica koje pokrivaju plohu lika.
Površina trokuta računa se prema formuli
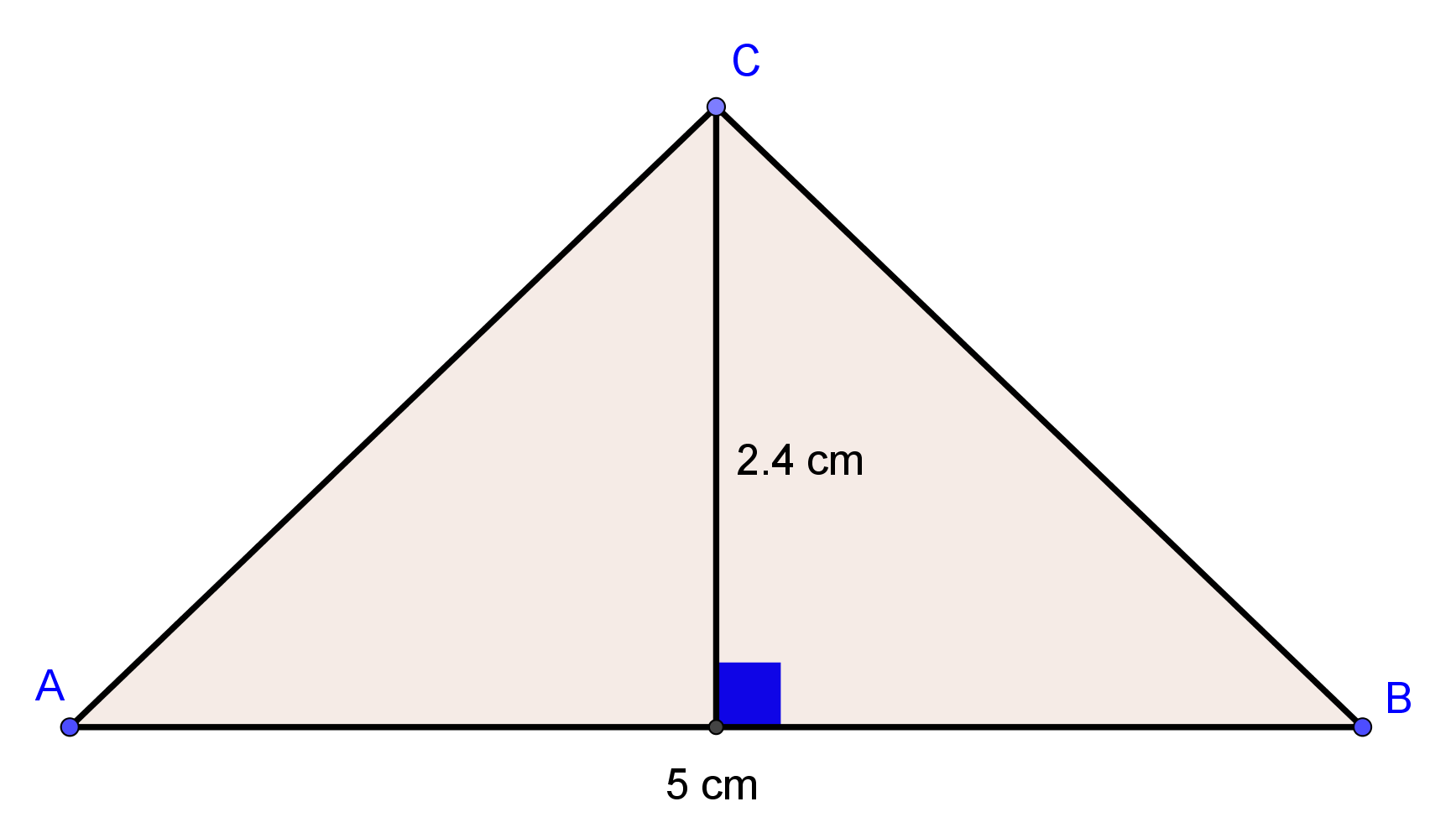
Površina trokuta sa slike je
Pomoć:
Zadani su slični trokuti i
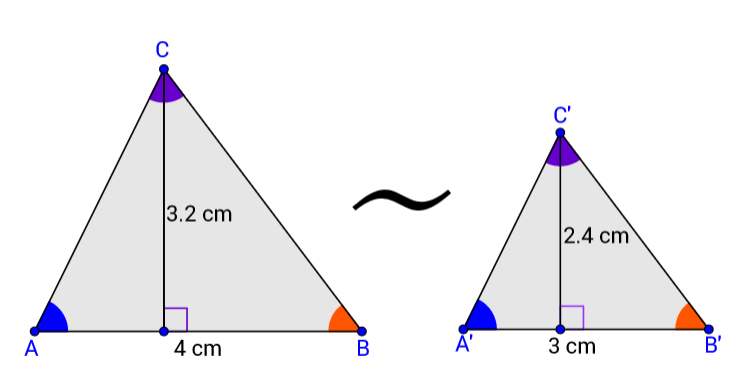
Izračunajte koeficijent sličnosti trokuta sa slike.
Pomoć:
Izračunajte omjer duljina odgovarajućih visina trokuta sa slike.
Pomoć:
Omjeri duljina odgovarajućih stranica i duljina odgovarajućih visina trokuta jednaki.
Pomoć:
Pažljivo pogledajte rješenja.
Organizirajte se u parove.
Nacrtajte dva slična trokuta na papir. Izmjerite duljine odgovarajućih stranica i izračunajte njihov omjer. Zatim izmjerite duljine pripadnih visina i izračunajte njihov omjer. Sve uredno zapišite u tablicu.
Ponovite postupak za sve tri stranice i sve tri pripadne visine tih trokuta.
Usporedite omjere.
Jeste li dobili iste vrijednosti omjera?
Možda vam zbog nepreciznog mjerenja omjeri budu približno, a ne potpuno isti. Možete zanemariti malu pogrešku.
Usporedite svoje zaključke s ostalim parovima u razredu.
Omjer odgovarajućih visina sličnih trokuta jednak je koeficijentu sličnosti tih trokuta.
Pomoć:
Omjer duljina odgovarajućih visina sličnih trokuta jednak je omjeru duljina odgovarajućih stranica tih trokuta.
Postupak:
Prisjetimo se mjernih jedinica za površinu.
Preračunajte i dovucite vrijednosti na njihove jednakosti.
|
|
|
|
|
|
|
|
|
Pomoć:
Trokuti na slici su slični.
Umnožak dvaju istih brojeva nazivamo kvadrat broja i pišemo
Zamijetimo da koeficijent sličnosti trokuta i omjer površina sličnih trokuta nisu jednaki. Kada pomnožimo koeficijent sličnosti sam sa sobom, dobijemo omjer površina sličnih trokuta,
Kažemo da je dobiveni omjer kvadrat koeficijenta sličnosti trokuta.
Provjerite vrijedi li tvrdnja i za druge slične trokute s pomoću interaktivne GeoGebrine simulacije.
U simulaciji uočite odgovarajuće kutove sličnih trokuta. Uočite omjere odgovarajućih stranica sličnih trokuta i provjerite je li omjer površina sličnih trokuta kvadrat omjera duljina stranica.
Omjer površina sličnih trokuta jednak je kvadratu koeficijenta sličnosti tih dvaju trokuta.
Možemo zapisati i ovako:
Ako za slične trokute
i
vrijedi
onda je i
ili
.
Primjer 3.
Ako nekom trokutu povećamo duljinu svake stranice puta, koliko će se puta povećati njegova površina?
Koeficijent označava koliko je puta slični trokut veći ili manji od početnog trokuta, znači da je koeficijent sličnosti u ovom primjeru
Omjer površina sličnih trokuta jednak je kvadratu koeficijenta pa izračunamo
Površina će se povećati
puta.
Ako nekom trokutu smanjimo duljinu svake stranice puta, koliko će se puta smanjiti njegova površina?
Pomoć:
Ako je koeficijent sličnosti dvaju trokuta koliki je koeficijent sličnosti njihovih površina?
Pomoć:
Primjer 4.
Odgovarajuće stranice dvaju sličnih trokuta odnose se kao Ako je površina većeg trokuta kolika je površina manjeg trokuta?
Ako je omjer duljina odgovarajućih stranica sličnih trokuta onda je omjer površina tih trokuta
Napišemo odgovarajući razmjer i dobijemo
Površina manjeg trokuta iznosi
Duljine odgovarajućih stranica sličnih trokuta iznose
i
Izračunajte površinu većeg trokuta ako je površina manjeg
Omjer duljina stranica je
Omjer površina je
Iz slijedi Za rješenje ovog zadatka preporučujemo da se koristite džepnim računalom.
Površina većeg trokuta iznosi
Opsezi sličnih trokuta odnose se kao Kolika je površina većeg trokuta ako je površina manjeg ?
Pomoć:
Postupak:
Mjerne jedinice za opseg su
Omjer opsega bilo kojih dvaju sličnih likova jednak je omjeru duljina odgovarajućih stranica tog lika.
Mjerne jedinice za površinu su
Omjer površina bilo kojeg lika jednak je kvadratu omjera duljina odgovarajućih stranica tog lika.

Obujam ili volumen je fizička veličina koja opisuje koliko tijelo zauzima prostora.
Mjerne jedinice za obujam su
Omjer obujama tijela istog oblika jednak je omjeru odgovarajućih duljina, visina ili širina tih tijela pomnoženih tri puta samih sa sobom.
U arhitektonskom studiju arhitektica je na papiru nacrtala tlocrt stana.
Mjerilo u kojem je nacrtan stan iznosi
Pomoć:
Postupak:
Pomoć:
Postupak:

Triangl je metalna udaraljka u obliku jednakostraničnog trokuta.
Pomoć:
Triangl ima sve tri stranice jednake duljine.
Duljina šipke je opseg jednakostraničnog trokuta.
Postupak:
Duljina stranice većeg triangla =
Koliko je puta opseg većeg trokuta dulji od manjeg toliko je puta i duljina odgovarajuće stranice većeg trokuta dulja od manje.

Jedra jedrilice su slični trokuti. Donja stranica većeg jedra duljine je a omjer duljina donjih stranica iznosi
Pomoć:
Pomoć:
Omjer duljina odgovarajućih stranica iznosi omjer površina iznosi
Postupak:
U tvornici igračaka izrađuju drvene pločice u obliku trokuta. Trenutačno izrađuju dvije veličine sličnih trokuta. Većem trokutu duljina osnovice iznosi a duljina visine na tu stranicu iznosi Omjer stranica tih trokuta iznosi
Površina većeg trokuta je
Iz 9 : 4 = 27 : slijedi
Površina većeg trokuta iznosi a površina manjeg trokuta iznosi
Za manju pločicu treba
boje, a za veću
boje.
Dio parka zasađen travom ima oblik jednakostraničnog trokuta površine
U sredini je ružičnjak istog oblika, ali duljine njegovih stranica triput su kraće.
Ako je stranica sličnog trokuta
puta kraća, onda je površina
puta manja.
Površina ružičnjaka iznosi
Zasađeno je ruža.
Primjer 5.
Površine sličnih trokuta iznose i Ako je duljina stranice manjeg trokuta kolika je duljina njoj odgovarajuće stranice većeg trokuta?
Ako je omjer površina trokuta tada je omjer duljina stranica jer je i
Iz razmjera dobijemo
Duljina odgovarajuće stranice većeg trokuta iznosi
Pomoć:
Postupak:
Površine sličnih trokuta iznose
i
Duljine stranica manjeg trokuta iznose
i
Izračunajte opseg većeg trokuta.
Omjer površina je
Koeficijent sličnosti trokuta je
Opseg manjeg trokuta iznosi
slijedi
Opseg manjeg trokuta iznosi
Pokušajte nacrtati tlocrt svoje sobe u omjeru
Ucrtajte i stvari koje se nalaze u sobi, primjerice krevet, stol i ormar.
Izmjerite potrebne veličine i izračunajte koliko „kvadrata” ima vaša soba.
Izrazite postotkom koliki dio površine sobe zauzima stol, koliki dio krevet, a koliki dio ormar.
Omjer opsega dvaju sličnih trokuta jednak je koeficijentu sličnosti tih dvaju trokuta.
Omjer površina dvaju sličnih trokuta jednak je kvadratu koeficijenta sličnosti tih dvaju trokuta. To možemo povezati s mjernim jedinicama, i tako lakše upamtiti. Opseg mjeri duljinu pa je mjerna jedinica opsega ista kao i mjerna jedinica duljine stranice. Površina je mjerni broj jediničnih kvadratića kojima možemo popločiti neku plohu. Ploha ima duljinu i širinu pa je mjerna jedinica za površinu umnožak istovrsnih mjernih jedinica, odnosno kvadrat mjerne jedinice za duljinu.
Za kraj procijenite svoje znanje kratkom provjerom.
Ako duljinu svake stranice trokuta povećamo
puta, opseg trokuta povećat će se
puta.
Pomoć:
Omjer opsega sličnih trokuta jednak je omjeru duljina odgovarajućih stranica sličnih trokuta.
Koliko će se puta smanjiti površina trokuta ako duljine svih njegovih stranica smanjimo puta?
Pomoć:
Omjer površina sličnih trokuta jednak je kvadratu koeficijenta sličnosti tih trokuta.
Postupak:
Duljine stranica većeg trokuta su Opseg njemu sličnog trokuta iznosi Izračunajte duljine stranica manjeg trokuta.
Dovucite stranice na njihove odgovarajuće duljine.
|
|
|
|
|
|
|
|
Pomoć:
Izračunajte opseg većeg trokuta.
Omjer opsega sličnih trokuta jednak je omjeru duljina odgovarajućih stranica sličnih trokuta.
Pomoć:
Omjer površina sličnih trokuta jednak je kvadratu koeficijenta sličnosti tih trokuta.
Postupak:
,
Pomoć:
Postupak:
,
Prometni znak u obliku jednakostraničnog trokuta pokraj autoceste ima duljinu stranice
a pokraj gradske ceste
Koliko je puta veća površina znaka pokraj autoceste od površine znaka pokraj gradske ceste?
Pomoć:
Omjer površina sličnih trokuta jednak je kvadratu koeficijenta sličnosti tih trokuta.
Postupak: