Matematika 7 - 7.8 Mnogokuti u svakodnevnom životu

Uređenje interijera

Zanimljivost

U svakodnevnom životu često imamo priliku čuti: Koliko kvadrata ima stan? Kvadrat stana stoji $1 000$ eura $(€) .$

Riječ kvadrat u ovim i sličnim primjerima ima značenje površine $1 m^{2} .$

Isto značenje ima i pojam četvorni metar, čiji naziv dolazi od četvorina, što znači kvadrat.

Kolekcija zadataka 1

Zadatak 1.

Martina mama u prizemlju obiteljske kuće želi urediti frizerski salon. Prednja ploha prostorije je ostakljena, a preostala tri zida i pod trebali bi izgledati kao na slici pronađenoj u jednom katalogu za uređenje interijera. Marta je pomogla mami izmjerivši dimenzije poda, a potom je izradila i skicu. Visina prostorije je $2.7 m .$

Proučite sliku iz kataloga i Martinu skicu pa zajedno s Martom izradite plan troškova i nabave potrebnog materijala.

Slika prikazuje unutrašnjost sobe bez namještaja

Slika prikazuje skicu tlocrta prostorije

a. Pod prostorije treba popločiti. Koliko je $m^{2}$ pločica potrebno za prekrivanje poda?

Da bismo odgovorili na postavljeno pitanje, moramo izračunati površinu poda koji je oblika pravokutnika kojemu je duljina $5.6 m,$ a širina $4 m .$ Pod ima površinu $22.4 m^{2}$ pa je potrebno i toliko kvadrata pločica.

b. Pločice koje je odabrala Martina mama kvadratnog su oblika duljine

40 cm,

a mogu se kupiti u paketu u kojemu je

15

pločica. Cijena jednog takvog paketa je

199.99 kn .

Koliko paketa treba kupiti i koliki će biti trošak?

Površina jedne pločice je $0.4 m \cdot 0.4 m = 0.16 m^{2} .$

Ako jedan paket sadrži $15$ pločica, površina svih pločica u paketu je $15 \cdot 0.16 m^{2} = 2.4 m^{2} .$

Da bismo saznali koliko nam je paketa potrebno, ukupnu površinu ćemo podijeliti s površinom koju čini jedan paket pločica. Pri dijeljenju dobijemo rezultat $9.3333.. .$

Treba li nam $9$ ili $10$ paketa?

Naravno, $10 .$ S devet paketa pločica ne bismo prekrili površinu cijeloga poda. Uostalom, zbog rezanja, pločica može puknuti pa će nam dobro doći koja pločica viška.

Odgovor na drugi dio pitanja sada je lako dati: $10 \cdot 199.99 kn = 1999.90 kn .$

Trošak za kupovinu pločica bit će približno dvije tisuće kuna.

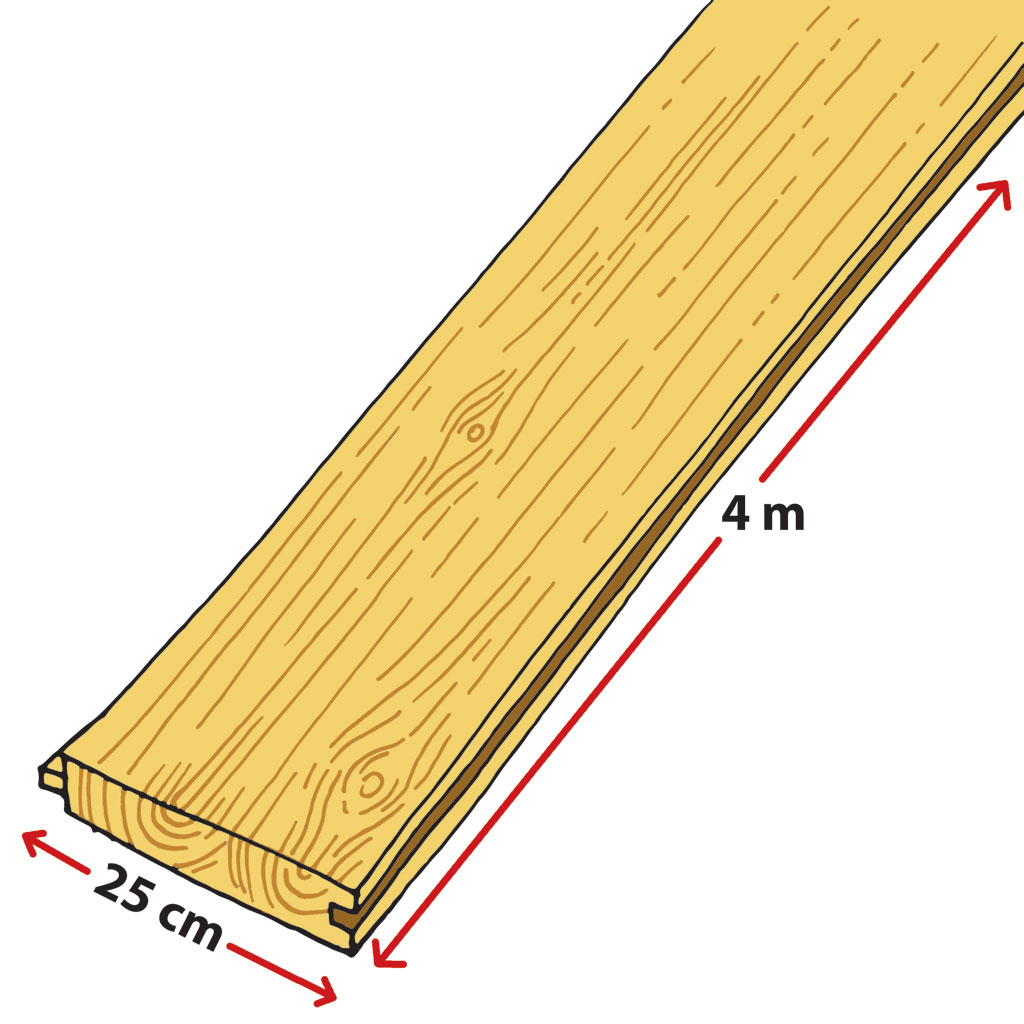
Slika prikazuje jednu dasku ariša koja služi za oblaganje zida ili slaganje ograde.

c. Martina mama zamislila je donji dio zidova obložiti daskama od ariša. Jedna je daska duga $4 m,$ a široka $25 cm .$ Na koliko dijelova je potrebno prerezati dasku ako visina drvene obloge treba biti $1 m ?$

Jednu dasku podijelit ćemo na

4

dijela, od kojih je svaki duljine

1 m .

d. Kolika je površina zida koju treba obložiti daskama ariša?

Lijevi i desni zid imaju duljinu $4 m,$ a preostali zid ima duljinu $5.6 m .$ Kako je visina jednaka $1 m,$ vrijedi

$\begin{array}{l} P = 4 \cdot 1 + 4 \cdot 1 + 5.6 \cdot 1 = (4 + 4 + 5.6) \cdot 1 = 13.6 \end{array},$

tj. površina koju je potrebno prekriti daskama je $13.6 m^{2} .$

e. Koliko je dasaka ariša potrebno kupiti da se obloži zid do visine $1 m ?$

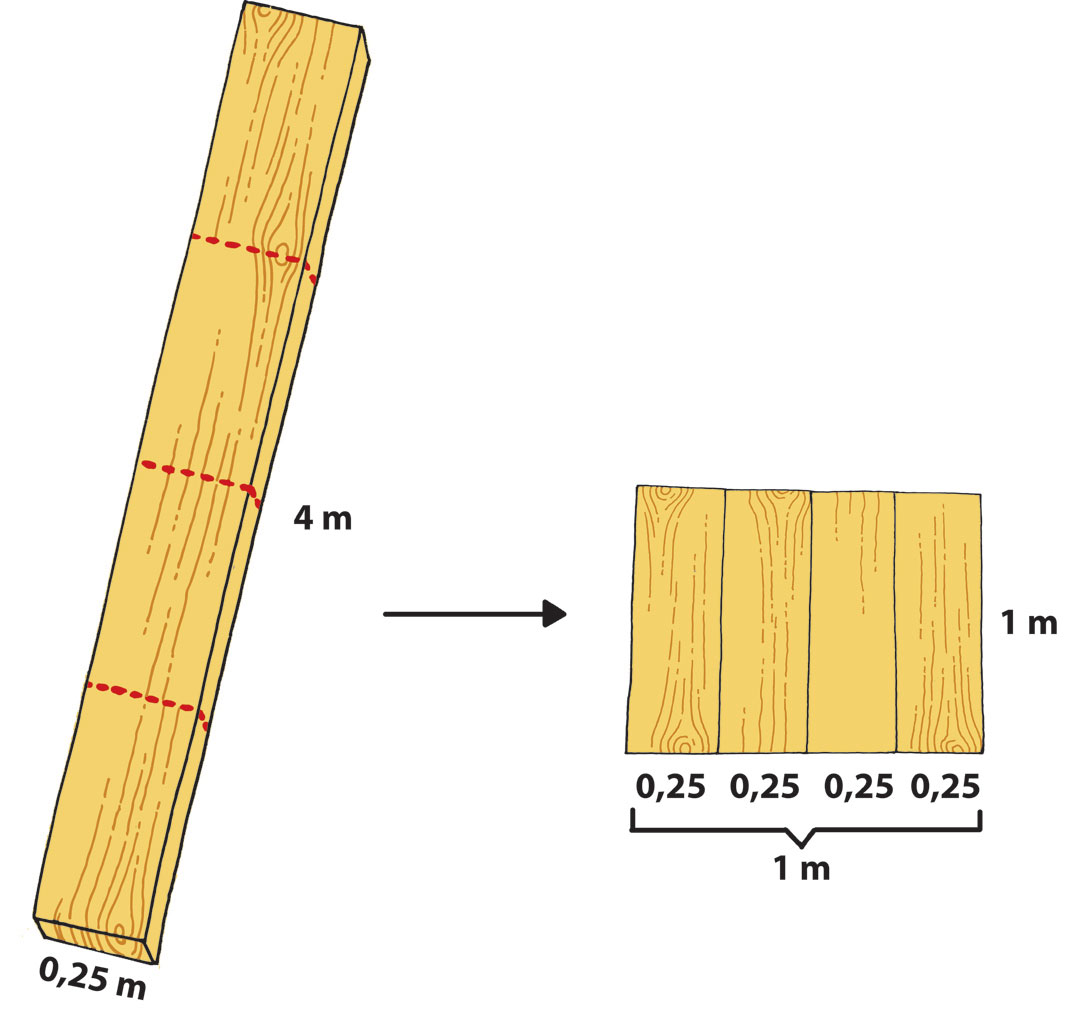
Slika prikazuje dasku ariša koju smo izrezali na 4 jednaka dijela i složili ju u kvadrat.

Površina koju možemo prekriti jednom daskom je $1 m^{2},$ a ukupno moramo pokriti $13.6 m^{2} .$ Iz toga slijedi da nam je potrebno $14$ dasaka.

f. Ako je cijena jedne daske $74 kn,$ koliki će biti trošak nabave za drvenu oblogu?

S obzirom na to da nam je potrebno $14$ dasaka, trošak ćemo izračunati množenjem cijene jedne daske s brojem dasaka. Trošak iznosi $1036 kn .$

g. Ostatak zida, iznad drvene obloge, Martina mama odlučila je obojiti, umjesto staviti tapetu poput one u katalogu. Koliko kvadrata treba obojiti?

Možemo računati površinu svakog zida posebno pa zbrojiti dobivene površine ili možemo zamisliti da smo sva tri zida razvili u jednu ravninu i na taj način dobili veliki pravokutnik kojem treba izračunati površinu.

Duljina pravokutnika je $(4 + 5.6 + 4) m = 13.6 m,$ a njegova visina je $(2.7 - 1) m = 1.7 m$ (jer je donji dio prekriven drvenom oblogom).

Površina zida koji treba obojiti je $13.6 m \cdot 1.7 m = 23.12 m^{2} .$

h. Martina mama odabrala je boju za zid koja se prodaje u pakiranjima od $2$ litre, $5$ litara ili $15$ litara. U uputama piše: "Potrošnja je $0.17 {l/m}^{2}$ - u dva sloja". Koje pakiranje i koliko njih treba kupiti za bojenje zida?

Ako je navedena potrošnja u litrama po metru kvadratnom, potrebno je broj kvadrata (površinu) pomnožiti s $0.17 :$

$23.12 m^{2} \cdot 0.17 \frac{l}{m^{2}} = 3.93 l,$ pa zaključujemo da je potrebno nešto manje od četiri litre boje.

S obzirom na ponuđena pakiranja, možemo uzeti ili $2$ pakiranja od $2 l$ ili jedno pakiranje od $5 l,$ ovisno o tome što je povoljnije.

i. Cijena pakiranja od $2 l$ iznosi $27.52 kn,$ a pakiranje od $5 l$ stoji $62 kn .$ Koliki će biti trošak nabave boje za zid?

Uzimajući u obzir rješenje zadatka e), možemo izračunati da dva manja pakiranja stoje približno $55 kn,$ što je svakako manje nego cijena jednog većeg pakiranja.

j. Koliki je ukupni trošak nabave materijala za uređenje poda i zidova frizerskog salona?

Podsjetimo se, Martina je mama kupila pločice za pod, daske ariša za oblaganje donjeg dijela zida i boju za bojenje ostatka zida.

materijal	$m^{2}$	približni trošak nabave ( $kn$ )
pločice	$22.4$	$2000$
daske ariša	$13.6$	$1036$
boja za zid	$23.12$	$55$
UKUPNO		$3091$

Zatvori

Zanimljivost

Prilikom odabira materijala za uređenje svakako je dobro potražiti više ponuda. Najbrže ćemo te podatke potražiti na mrežnim stranicama tvrtki koje se bave prodajom traženih materijala. Na stranicama nekih tvrtki može se pronaći kalkulator potrošnje prema kojemu možemo izračunati koliko npr. boje za zid treba kupiti ako znamo kvadraturu koju želimo obojiti.

Provjeri kalkulatorom potrošnje točnost izračuna zadatka h).

Praktična vježba

Sljedeća tri zadatka riješite uz pomoć interneta kao izvora informacija.

Provjerite cijenu rada za postavljanje pločica, oblaganje zidova te ličenje zida pa izračunajte trošak koji očekuje Martinu mamu.
Istražite naziv obrtnika (majstora) koji rade navedene poslove.
Istražite postoji li u vašem gradu (ili gradu koji je najbliži vašem mjestu stanovanja) srednja škola za navedena zvanja.

Vanjski radovi

Kolekcija zadataka 2

Zadatak 2.

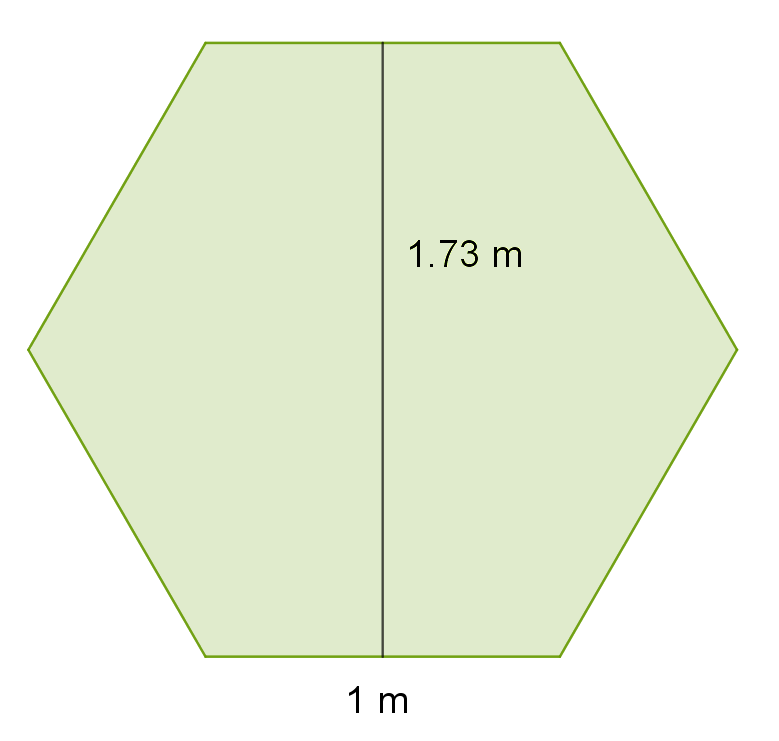
Slika prikazuje pravilni šesterokut s istaknutom duljinom stranice i udaljenosti dviju paralelnih stranica

U bakinu dvorištu je cvjetnjak u obliku pravilnog šesterokuta, kao na slici. Baka želi posaditi narcise i tulipane. To neće biti problem, jer baka zna da njihove lukovice može posaditi odjednom, samo na različite dubine. Međutim, baka nije sigurna koliko lukovica kojeg cvijeta mora kupiti. Dobila je savjet da posadi $40$ lukovica tulipana i $25$ lukovica narcisa na jedan četvorni metar.

Kako bi baka riješila problem, treba znati cvjetnjaka.

null

null
Odaberite ispravan redoslijed radnji za izračunavanje površine bakina cvjetnjaka.
Podijelit ćemo zadani lik na likove čije površine znamo izračunati.

Izračunat ćemo površine pojedinih likova.

Zbrojit ćemo površine dijelova kako bismo dobili površinu cjeline.
null

null
Površina bakina cvjetnjaka iznosi $m^{2} .$

Pomoć:

Najučinkovitije je pravilni šesterokut podijeliti na šest sukladnih trokuta ili na dva sukladna trapeza. Uz zadane dimenzije nije teško izračunati površinu jednog trokuta ili jednog trapeza.

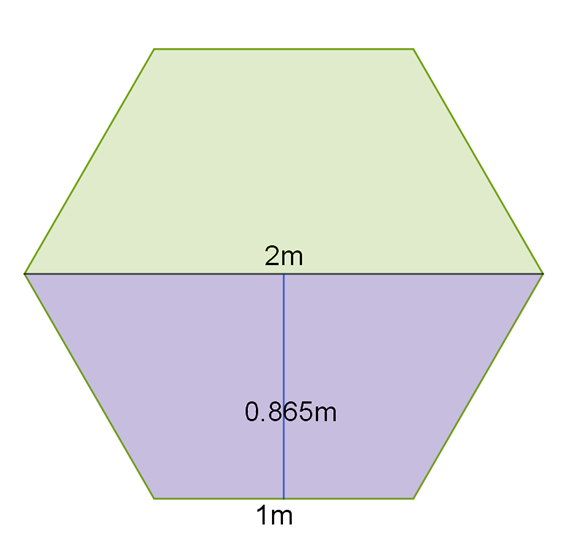
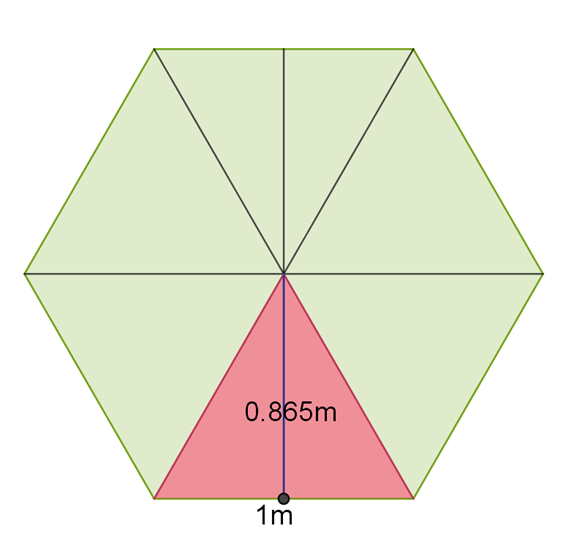
Postupak:

Prvi način:

$P_{t r o k u t a} = \frac{1 \cdot 0.865}{2} = 0.4325$

pa je površina šesterokuta šest puta veća tj.

$P = 2.595 m^{2} \approx 2.6 m^{2},$

ili drugi način:

$P_{t r a p e z a} = \frac{1 + 2}{2} \cdot 0.865 = 1.2975$

pa je površina šesterokuta dva puta veća

$P = 2.595 m^{2} \approx 2.6 m^{2}$
Koliko baka treba zasaditi lukovica tulipana, a koliko lukovica narcisa?

$15$ lukovica tulipana i $10$ lukovica narcisa

$65$ lukovica tulipana i $104$ lukovice narcisa

$104$ lukovice tulipana i $65$ lukovica narcisa

Pomoć:

Prisjetite se proporcionalnih veličina.

Postupak:

Tulipani: ako za $\begin{array}{l} 1 m^{2} \end{array}$ treba $40$ lukovica, za $\begin{array}{l} 2.6 m^{2} \end{array}$ trebat će $2.6$ puta više, tj. $104$ lukovice. Narcisi: ako za $\begin{array}{l} 1 m^{2} \end{array}$ treba $25$ lukovica, za $\begin{array}{l} 2.6 m^{2} \end{array}$ trebat će $2.6$ puta više, tj. $65$ lukovica.
Osim što voli cvijeće, baka voli i svojega Garu. No i Garo voli cvijeće! Baka uistinu ne voli vidjeti Garu u cvjetnjaku pa je odlučila ograditi cvjetnjak. Da bi ogradila cvjetnjak, baki je potrebno metara ograde.

Pomoć:

Ogradu postavljamo po rubu cvjetnjaka, a duljina ruba predstavlja opseg lika.

Postupak:

Opseg lika je zbroj duljina svih njegovih stranica.

Zadatak 3.

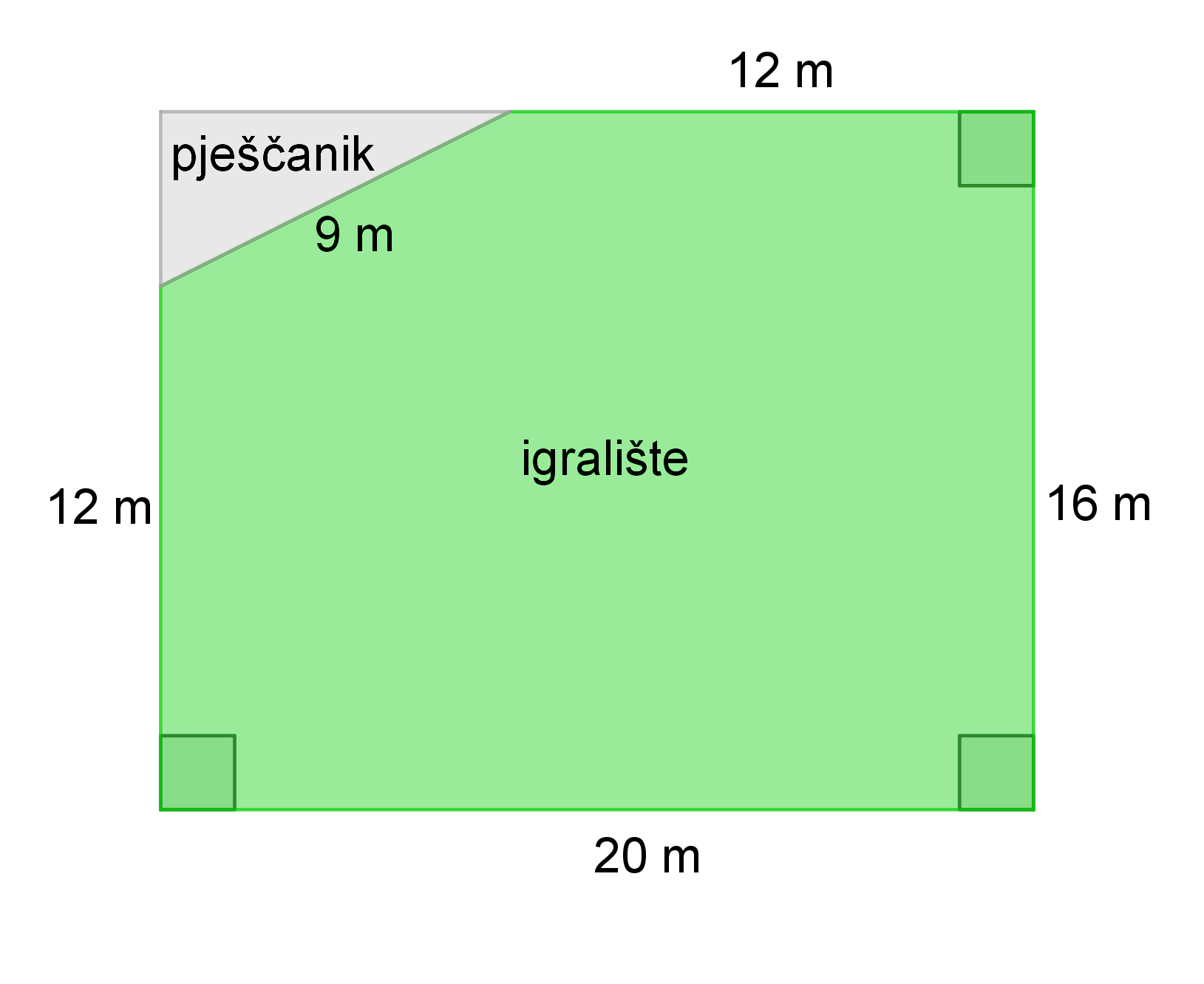
Slika prikazuje tlocrt igrališta s upisanim dimenzijama

Na sastanku mjesnog odbora odlučeno je da će na dijelu dječjeg igrališta napraviti pješčanik za malu djecu. Nakon rasprave, donesena je i odluka o njegovoj veličini. Proučite tlocrt igrališta i odgovorite na sljedeća pitanja.

Kolika je površina pješčanika iskazana u $m^{2} ?$

$21$

$32$

$16$

Pomoć:

Pješčanik ima oblik pravokutnog trokuta. Izračunaj duljine njegovih kateta, a zatim izračunaj površinu.

Postupak:

Katete pravokutnog trokuta duge su $8 cm$ i $4 cm$ pa površina iznosi $16 {cm}^{2} .$
Koliki je dio prvotnog igrališta zauzeo pješčanik?

dvadesetinu

desetinu

petinu

Pomoć:

Površina pješčanika je $16 m^{2}$ , a površina prvotnog igrališta $320 m^{2}$ $.$

Postupak:

$\frac{16}{320} = \frac{1}{20}$
Izračunajte površinu travnatog dijela igrališta na barem dva različita načina. Tražena površina iznosi $m^{2} .$

Pomoć:

Najjednostavniji način je da od površine prvotnog igrališta oduzmemo površinu pješčanika, a drugi da travnati dio podijelimo na likove kojima možemo izračunati površinu, npr. pravokutnik i trapez.

Zatvori

Kutak za znatiželjne

Riješite prethodni zadatak koristeći se predloškom GeoGebre.

Koristeći se alatom za crtanje mnogokuta, nacrtajte pravokutnik zadanih dimenzija (predlažemo omjer: jedna stranica kvadratića neka predstavlja $4 m,$ tj. možemo govoriti o omjeru $1 : 4,$ ako radi jednostavnosti zamislimo da su dimenzije u metrima).
Koristeći se istim alatom, nacrtajte trokut, kao na slici.
U algebarskom prozoru očitajte površine nacrtanih mnogokuta.
Primjenjujući znanje o površini sličnih likova, izračunajte tražene površine.

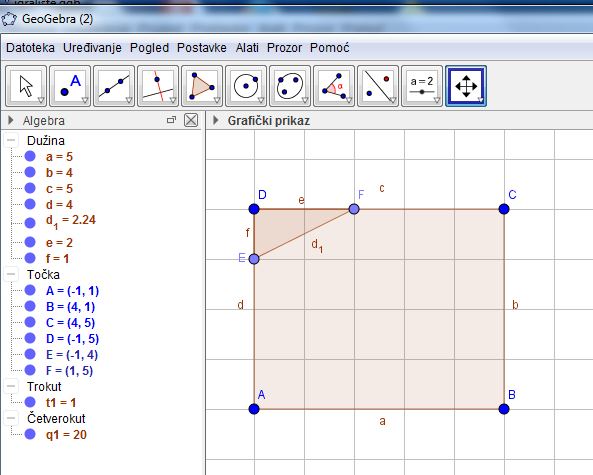
Slika prikazuje crtež igrališta u koordinatnoj mreži

U algebarskom prozoru očitavamo površinu pravokutnika $20$ (i smatramo da se radi o $m^{2}$ ). Koeficijent sličnosti u našem je slučaju $k = 4$ pa ćemo traženu površinu izračunati kao $P = 20 \cdot 4^{2},$ jer se površine sličnih likova odnose kao kvadrat koeficijenta sličnosti.

Izračunavamo da je $P = 320 m^{2} .$

Na isti način očitavamo i računamo površinu trokuta (pješčanika).

Slikanje krpicama

Zanimljivost

Slika prikazuje prekrivač izrađen patchwork tehnikom

Patchwork je vrlo zanimljiva tehnika šivanja u kojoj se različiti komadići tkanina spajaju u jedinstvenu cjelinu, prateći određene uzorke. Najbliži prijevod na hrvatski jezik bio bi krpljenje, no mnogima je draži naziv slikanje krpicama.

Zadatak 4.

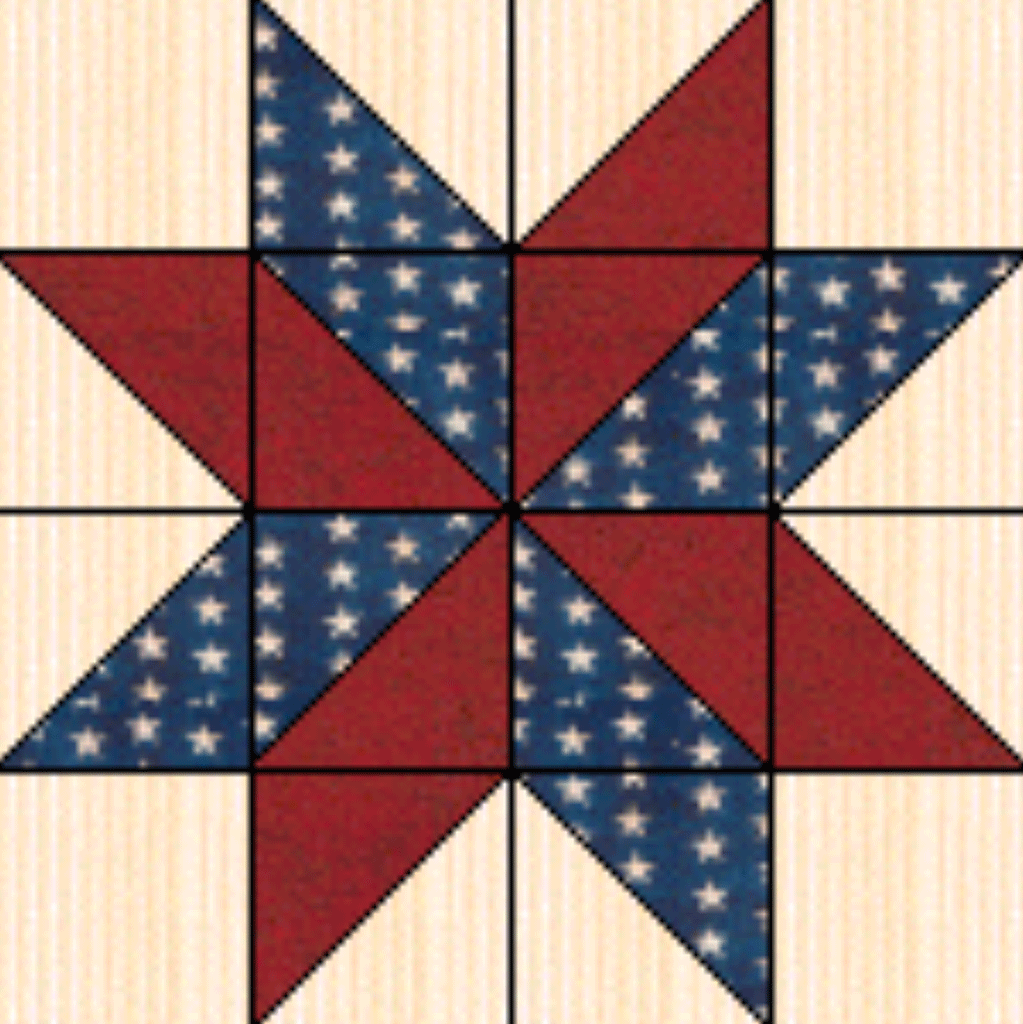
Slika prikazuje uzorak za patchwork u obliku zvijezde

Dora je kod bake našla punu kutiju raznobojnih krpica, ostataka od šivanja. Domislila se: zamolit će baku da joj pomogne napraviti dekicu za svojega tek rođenog brata. Na internetu je pronašla razne uzorke, ali najviše joj se svidio ovaj nacrtan u mreži koju čini $16$ kvadratića sa stranicom od $5 cm .$ Odlučila je da će osnovna boja biti žuta. Plavog tekstila s točkicama ima dovoljno, a crveni dio zamijenit će šarenim krpicama.

a. Dekica bi trebala imati dimenzije $80 \times 120 (cm) .$ Koliko kvadrata poput nacrtanog uzorka treba izraditi?

Ako kvadratić ima stranicu duljine $5 cm,$ tada je stranica uzorka (kvadrata) $20 cm .$ Želimo li da dekica ima širinu $80 cm,$ potrebno je složiti četiri takva kvadrata. Za duljinu je potrebno šest velikih kvadrata, jer dekica treba biti dugačka $120 cm .$

Dakle, šest puta po četiri kvadrata iznosi $24$ kvadrata.

b. Koliko treba pripremiti žute tkanine?

Promatramo li uzorak, primjećujemo da dva trokuta imaju jednaku površinu kao kvadratić, $25 {cm}^{2} .$ Prebrojavanjem možemo otkriti da je takvih površina osam, što ukupno iznosi $200 {cm}^{2} .$ Uvažavajući rješenje zadatka a), možemo izračunati da je ukupno potrebno $24 \cdot 200 {cm}^{2},$ što iznosi $4800 {cm}^{2} .$

Potrebno je pripremiti $m^{2}$ žute tkanine.

null

null

d. Možete li zaključiti, bez izračunavanja površine tkanine, koliki dio jednog kvadrata (uzorka) čini plavi (točkasti) dio?

Utvrdili smo da u jednom kvadratu (uzorku) ima osam žutih kvadratića (gdje smo računali da dva trokuta čine jedan kvadratić). S obzirom na to da ukupno ima $16$ kvadratića, plavi i šareni čine polovinu kvadrata. A kako su to sukladni likovi, zaključujemo da plava tkanina čini četvrtinu kvadrata.

Izradi vježbu

Ukrasno-uporabni predmet sašiven patchwork tehnikom može biti idealan poklon za nekog vama bliskog. Osmislite i nacrtajte uzorak kakav biste voljeli izraditi i okušajte se u slikanju krpicama. Detalje o tehnici šivanja i ideje lako ćete pronaći uz pomoć internetskog pretraživača.

Tangram

Kolekcija zadataka 3

Zadatak 5.

Tangram se sastoji od sedam dijelova: pet jednakokračnih pravokutnih trokuta (od kojih su dva para sukladna), jednog kvadrata i jednog paralelograma. Prema predlošku složite elemente tangrama tako da prekriju površinu zadanog kvadrata a da se međusobno ne preklapaju.

Zadatak 6.

Od tri dijela tangrama (dva mala trokuta i onaj srednji) složi sljedeće likove: kvadrat, pravokutnik, trapez, trokut i paralelogram.

Možete se koristiti danim predloškom ili ga izraditi od tvrdog papira prema uputama koje možete naći u Izradi vježbu.

Slika prikazuje kvadrat, pravokutnik, paralelogram, trapez i trokut složene od dijelova tangrama

Zatvori

Zanimljivost

Ako želite, možete zaigrati edukativnu igricu na engleskom jeziku Četiri dijela tangrama.

Izradi vježbu

Da biste sami napravili tangram, potreban vam je karton ili tvrdi papir u boji. Položite ga na stol tako da naličje bude okrenuto prema gore.

Slijedite upute:

Nacrtajte kvadrat $A B C D$ duljine stranice $16 cm .$
Nacrtajte dijagonalu $\bar{B D} .$
Nacrtajte dio dijagonale $\bar{A C},$ od vrha $C$ do sjecišta dviju dijagonala $S .$
Polovišta dužina $\bar{A B},$ $\bar{A D},$ $\bar{S B},$ $\bar{S D}$ i $\bar{E F}$ označite redom $E,$ $F,$ $G,$ $H$ i $I .$
Nacrtajte dužine $\bar{I H},$ $\bar{I S},$ $\bar{E G} .$
Izrežite trokute $△ D S C,$ $△ S B C,$ $△ A E F,$ $△ S H I,$ $△ E B G,$ kvadrat $E G S I$ i paralelogram $F I H D .$
Okrenite sve dijelove tako da prednja strana bude okrenuta prema gore (kako se ne bi vidjeli tragovi olovke).

Taj tangram može vam poslužiti i kao model, kako biste prema njemu izrezali raznobojne tangrame.

Praktična vježba

Osmislite sami zadatak u kojemu treba primijeniti znanje o opsegu i površini mnogokuta.

7.8 Mnogokuti u svakodnevnom životu

Na početku...

Zanimljivost

Uređenje interijera

Zanimljivost

Kolekcija zadataka 1

Zadatak 1.

Zanimljivost

Praktična vježba

Vanjski radovi

Kolekcija zadataka 2

Zadatak 2.

Zadatak 3.

Kutak za znatiželjne

Slikanje krpicama

Zanimljivost

Zadatak 4.

Izradi vježbu

Tangram

Kolekcija zadataka 3

Zadatak 5.

Zadatak 6.

Zanimljivost

Izradi vježbu

Praktična vježba

...i na kraju