Matematika 7 - 3.5 Primjena postotnog računa

Sniženje i poskupljenje

Izvor videozapisa: Državni zavod za statistiku

Primjer 1.

U katalogu piše da je cijena kozjeg sira snižena $15 % .$ Ako je cijena prije sniženja bila $120.00 kn$ po kilogramu, kolika je nova cijena tog sira?

Primjer se može riješiti na dva načina.

Prvi način:

Početna cijena sira je $120.00 kn .$

$15 %$ od $120 kn$ je $0.15 \cdot 120 = 18 kn$ $.$

Ovdje se radi o sniženju pa početnu cijenu moramo umanjiti za postotni iznos.

Od početne cijene $120 kn$ oduzmemo postotni iznos $18 kn,$ $120 - 18 = 102 kn$ $.$

Nova cijena sira je $102 kn$ po kilogramu.

Slika prikazuje dva stupčasta dijagrama. DIjagrami su u obliku kovanica poslaganih jedna na drugu. Zaključujemo kako je sniženje 15 %.

Drugi način:

Možemo li do nove cijene doći brže?

Pogledajmo što se događa s veličinama.

Stara cijena je osnovna vrijednost, cjelina, $100 % .$

Novu cijenu dobili smo tako što smo od stare cijene oduzeli postotni iznos.

Novu cijenu dobijemo kad od $100 %$ oduzmemo $15 %$ stare cijene.

Matematički bismo to zapisali ovako:

Nova cijena je ( $100 % - 15 %$ ) od stare cijene.

Nova cijena je $85 %$ stare cijene.

Nova cijena $y = 0.85 \cdot 120 .$

Nova cijena $y = 102 kn .$

Nova cijena sira je $102 kn$ po kilogramu.

Ako smo početnu cijenu, osnovnu vrijednost $x$ smanjili za $p %,$ novu cijenu ili novi postotni iznos $y$ dobijemo tako da pomnožimo početnu cijenu ili osnovnu vrijednost $x,$ s postotkom $(100 % - p %) .$

Formula za postotni račun kod sniženja:

Osnovna vrijednost $x$ je početna cijena od koje računamo sniženje za $p % .$

Novi postotni iznos je $y .$

Postotak koji odgovara sniženoj cijeni je $(100 % - p %) .$

Cijenu nakon sniženja dobijemo tako da pomnožimo početnu cijenu s postotkom $(100 % - p %) .$

$y = (100 % - p %) \cdot x$

Zanimljivost

Promjena cijene kod sniženja za $p % :$

Nova cijena je $(100 % - p %)$ od početne cijene.

Zadatak 1.

Cijena cipela snižena je za $45 % .$ Kolika je nova cijena cipela ako su prije sniženja stajale $350 kn ?$

Procijenite novu cijenu, izračunajte pa usporedite točno rješenje sa svojom procjenom.

Slika prikazuje dva stupčasta dijagrama. DIjagrami su u obliku kovanica poslaganih jedna na drugu. Zaključujemo kako je sniženje za 45 %

Pri procjeni se prisjetite da je $45 %$ malo manje od $50 %$ pa bi nova cijena mogla biti približno polovica početne cijene, dakle malo viša od $175 kn .$

Početna cijena $x = 350 kn .$

$p % = (100 % - 45 %) = 55 % .$

$y = 350 \cdot 55 %$

$y = 350 \cdot 0.55$

$y = 192.50 kn .$

Nova je cijena $192.50 kn .$

Primjer 2.

Nakon sniženja od $20 %,$ nova cijena prijenosnog punjača za mobitel je $100.00 kn .$ Kolika je bila cijena punjača prije sniženja?

Procijenite početnu cijenu, pogledajte rješenje primjera pa usporedite svoju procjenu s rješenjem.

$20 %$ je petina početne cijene, ne znamo početnu cijenu, ali za procjenu nam može poslužiti i cijena nakon sniženja. Zaključujemo da je prije cijena bila otprilike $20 kn$ viša, dakle početna je cijena bila oko $120 kn .$

U ovom nam je zadataku poznata nova cijena, a tražimo početnu cijenu.

Cijena nakon sniženja je $100 kn .$

Postotak koji odgovara sniženoj cijeni $(100 % - 20 %) = 80 % .$

Cijenu nakon sniženja $y$ dobijemo tako da pomnožimo $(100 % - 20 %)$ s početnom cijenom $x,$ $y = 80 % \cdot x,$

$100 = 0.8 \cdot x,$

$x = 100 : 0.8$

$x = 125 kn .$

Cijena punjača prije sniženja bila je $125 kn .$

Početnu cijenu $x$ dobijemo tako da podijelimo novu cijenu $y$ s postotkom koji odgovara sniženoj cijeni $(100 % - p %) .$

Početna cijena kod sniženja::Početnu cijenu, tj. osnovnu vrijednost $x$ kod sniženja za $p %$ dobijemo tako da podijelimo novu cijenu, tj. postotni iznos $y$ koji smo dobili nakon sniženja, s postotkom koji odgovara sniženoj cijeni $(100 % - p %) .$

Zadatak 2.

Cijena televizora nakon sniženja za $40 %$ je $2 010.00 kn .$ Kolika je bila cijena tog televizora prije sniženja?

Procijenite početnu cijenu, izračunajte pa usporedite točno rješenje sa svojom procjenom.

Nova je cijena dobivena sniženjem $40 % .$ Kako je $100 % - 40 % = 60 %,$ nova je cijena $60 %$ početne cijene.

Nova cijena $y = 2 010 kn$ je $60 %$ od $x .$ Zapišimo još i $60 %$ u obliku decimalnog broja i uvrstimo u osnovnu formulu za izračunavanje postotka.

$y = 0.6 \cdot x$

$2 010 = 0.6 \cdot x$

$x = 2 010 : 0.6$

$x = 3 350 kn$

Cijena televizora prije sniženja bila je $3 350 kn .$

Primjer 3.

Hlače su prije sniženja stajale $250.00 kn,$ a poslije sniženja stoje $205.00 kn .$ Koliki je postotak sniženja cijene tih hlača?

Primjer se može riješiti na dva načina.

Prvi način:

Izračunamo razliku početne cijene i nove cijene.

$250 kn - 205 kn = 45 kn .$ Ta razlika je postotni iznos koji dobijemo kad računamo za koliko se promijenila cijena pri sniženju od $p % .$

$p % = 45 : 250$

$p % = 0.18$

$p % = 18 %$

Postotak sniženja je $18 % .$

Drugi način:

Primjer smo mogli riješiti i na drugi način.

Nova cijena je postotni iznos $y = 205 kn .$

Početna cijena je osnovna vrijednost $x = 250 kn .$

Novu cijenu $y$ kod sniženja dobijemo tako da pomnožimo početnu cijenu $x$ s postotkom koji odgovara sniženoj cijeni $(100 % - p %) .$

$y = (100 % - p %) \cdot x$

$205 = (100 % - p %) \cdot 250$

$100 % - p % = 205 : 250$

$100 % - p % = 0.82$

$100 % - p % = 82 %$

$p % = 100 % - 82 %$

$p % = 18 %$

Postotak sniženja je $18 % .$

Kad želimo izračunati postotak sniženja, možemo to učiniti na dva načina.

Prvi je da izračunamo razliku između početne cijene $x$ i nove cijene $y,$ pa tu razliku podijelimo s početnom cijenom i pomnožimo sa $100$ kako bismo dobiveni broj zapisali u postotnom obliku.

Drugi je da podijelimo novu cijenu $y$ s početnom cijenom $x,$ rješenje pomnožimo sa $100$ da bismo ga zapisali u postotnom obliku i onda oduzmemo dobiveni postotak od $100 % .$

Možete birati način na koji ćete računati postotak sniženja.

Kolekcija zadataka 1

Zadatak 3.

Perilica posuđa je prije sniženja stajala $4 520.00 kn,$ a poslije sniženja stoji $2 486.00 kn .$ Koliki je postotak sniženja cijene te perilice?

Postotak procijenite, izračunajte pa usporedite svoju procjenu s točnim rješenjem.

$2 486$ je malo više od polovine $4 520$ pa je postotak sniženja malo veći od $50 %,$ a postotak koji odgovara sniženoj cijeni malo manji od $50 %$ jer je on $100 % - p % .$

Nova je cijena $y = 2 486 kn,$ početna je cijena $x = 4 520 kn .$

$100 % - p % = 2 486 : 4 520$

$100 % - p % = 0.55$

$100 % - p % = 55 %$

$p % = 100 % - 55 %$

$p % = 45 %$

Cijena perilice posuđa snižena je za $45 % .$

Zadatak 4.

U trgovini zdravom prehranom Mirna je uz popust na gotovinu od $36 %$ kupila žitarice za $48.00 kn .$ Koliko bi platila te žitarice bez popusta?

Osnovna vrijednost i postotni iznos su proporcionalne veličine pa zadatke možemo rješavati i s pomoću razmjera.

Cijena s popustom je postotni iznos $y = 48 kn .$

Cijena bez popusta je početna cijena, osnovna vrijednost $x kn .$

Riječ je o popustu, sniženju cijene pa je postotak koji odgovara novoj cijeni:

$100 % - 36 % = 64 % .$

Za postotni iznos i osnovnu vrijednost vrijedi razmjer:

postotni iznos : osnovna vrijednost = postotak : $100 .$

Zapišemo li to u kontekstu cijena, imamo: nova cijena : početna cijena = postotak : $100 .$

$48 : x = 64 : 100$

$64 x = 4 800$

$x = 75 kn .$

Bez popusta, Mirna bi žitarice platila $75 kn .$

Zadatak 5.

U trgovačkom su centru izradili novi katalog redovitih cijena, postotka sniženja i sniženih cijena. Popunite katalog. Pripazite kad upisujete cijene. Cijene se pišu u obliku decimalnog broja zaokruženog na dvije decimale.

Cijene upišite u obliku decimalnog broja s dvije decimale, a postotak u obliku prirodnog broja na isprekidane linije. Točnost rješenja provjerite klikom na ljubičastu kvačicu. Interaktivni zadatak riješite u $10$ pokušaja, a kada ga uspješno riješite pojaviti će Vam se novi letak.

Zatvori

Primjer 4.

Račun za struju u jednom kućanstvu u lipnju iznosi $230.00 kn .$ Uz uvjet da je potrošnja u srpnju ista, koliko bi iznosio račun tog kućanstva u srpnju ako je struja poskupjela za $2.4 % ?$

Primjer se može riješiti na dva načina.

Prvi način:

Osnovna vrijednost u zadatku je iznos računa u lipnju, $230 kn .$ Od toga računamo $2.4 % .$

$230 \cdot 2.4 % = 230 \cdot 0.024 = 5.52 kn$

Postotni iznos je $5.52 kn .$

Sada se radi o poskupljenju pa početni iznos računa moramo povećati za postotni iznos.

Osnovnoj vrijednosti dodamo postotni iznos $5.52 kn$ , $230.00 + 5.52 = 235.52 kn$ $.$

Račun za struju u srpnju iznosit će $235.52 kn .$

Drugi način:

Možemo li do novog iznosa računa doći brže? Zadatak možete riješiti i s pomoću trojnog pravila.

Pogledajmo što se događa s veličinama.

Osnovna vrijednost je cjelina pa početnom iznosu računa odgovara $100 % .$

Novi iznos računa, u srpnju, dobili smo tako da smo iznosu računa u lipnju dodali postotni iznos.

Novi iznos računa dobijemo kad na $100 %$ dodamo $2.4 %$ iznosa računa u lipnju.

Matematički bismo to zapisali ovako:

Novi iznos računa je $(100 % + 2.4 %)$ od iznosa računa u lipnju.

Novi iznos računa je $102.4 %$ od iznosa računa u lipnju.

Novi iznos računa $y = 102.4 % \cdot 230 .$

$y = 1.024 \cdot 230$

$y = 235.52$

Iznos računa za struju u srpnju je $235.52 kn .$

Ako smo početni iznos računa, osnovnu vrijednost $x$ povećali za $p %,$ novi iznos računa ili novi postotni iznos $y$ dobijemo tako da pomnožimo početnu cijenu, tj. osnovnu vrijednost $x,$ s postotkom $(100 % + p %) .$

Osnovna vrijednost $x$ je početna cijena od koje računamo poskupljenje za $p % .$

Nova cijena, tj. novi postotni iznos je $y .$

Postotak koji odgovara cijeni nakon povećanja je $(100 % + p %) .$

Novu cijenu dobijemo tako da pomnožimo početnu cijenu s postotkom $(100 % + p %) .$

$y = (100 % + p %) \cdot x$

Zanimljivost

Promjena cijene kod poskupljenja za $p % :$

Nova je cijena $(100 % + p %)$ od početne cijene.

Zadatak 6.

Cijena kišobrana je $55.00 kn .$ Kolika je nova cijena ako se cijena kišobrana povisila za $30 % ?$

Slika prikazuje dva stupčasta dijagrama. DIjagrami su u obliku kovanica poslaganih jedna na drugu. Zaključujemo kako je poskupljenje 30%

Osnovna vrijednost, tj. početna cijena je $55 kn .$

$y = (100 % + 30 %) \cdot 55$

$y = 130 % \cdot 55$

$130 % = 1.3$

$y = 1.3 \cdot 55$

$y = 71.50 kn$

Nova je cijena kišobrana $71.50 kn .$

I druge veličine, osim cijena, mogu se umanjivati ili uvećavati za neki postotak.

Promjena veličine kod smanjenja za $p % :$ postotni iznos je $(100 % - p %)$ od osnovne vrijednosti.

Nova je vrijednost $(100 % - p %)$ od početne vrijednosti.

Promjena veličine kod povećanja za $p % :$ postotni iznos je $(100 % + p %)$ od osnovne vrijednosti.

Nova je vrijednost $(100 % + p %)$ od početne vrijednosti.

Zadatak 7.

Na izbore su ove godine izišla $120 043$ stanovnika jednoga grada. U odnosu prema prošloj godini, to je povećanje od $23 % .$ Koliko je građana prošle godine izišlo na izbore?

Najprije procijenite rješenje, zatim svoju procjenu usporedite s točnim rješenjem.

Slika prikazuje dva stupčasta dijagrama. DIjagrami su u obliku niza šarenih silueta poslaganih jedne na druge. Zaključujemo kako je povećanje 23%

$23 %$ je približno $20 %,$ dakle petina ukupnog broja građana. Smanjimo li $120 000$ za petinu, dobit ćemo približno $100 000$ građana.

Novi broj stanovnika, tj. postotni iznos je $120 043$ građana.

$x = y : 123 %$

$x = 120 043 : 1.23$

$x = 97 596$ građana

Rješenje zaokružimo na cijeli broj jer je riječ o broju stanovnika.

Prošle je godine u tom gradu na izbore izišlo $97 596$ građana.

Osnovnu vrijednost $x$ kod povećanja za $p %$ dobijemo tako da podijelimo postotni iznos $y$ koji smo dobili nakon povećanja s postotkom. $(100 % + p %.)$

$x = y : (100 % + p %)$

Zadatak 8.

Za koliko je posto viša cijena printera ako je početna cijena bila $450.00 kn,$ a nova je cijena $495.00 kn ?$

Najprije procijenite rješenje, zatim svoju procjenu usporedite s točnim rješenjem.

Zadatak možete riješiti na dva načina.

Prvi način:

Zamijetimo da je razlika između nove i stare cijene $45 kn .$

$p % = 45 : 450$

$p % = 0.1$

$p % = 10 %$

Postotak poskupljenja je $10 % .$

Drugi način:

Zadatak smo mogli riješiti i na drugi način.

Nova cijena je postotni iznos $y = 495 kn .$

Početna cijena je osnovna vrijednost $x = 450 kn .$

Novu cijenu $y$ pri poskupljenju dobijemo tako da pomnožimo početnu cijenu $x$ s postotkom koji odgovara cijeni nakon poskupljenja $(100 % + p %) .$

$y = (100 % + p %) \cdot x$

$495 = (100 % + p %) \cdot 450$

$(100 % + p %) \cdot 450 = 495$

$100 % + p % = 495 : 450$

$100 % + p % = 1.1$

$100 % + p % = 110 %$

$p % = 110 % - 100 %$

$p % = 10 %$

Postotak poskupljenja je $10 % .$

U ovom slučaju nam je prvi način bio jednostavniji.

Postotak $p %$ povećanja početne vrijednosti (osnovne vrijednosti) $x$ na novu vrijednost (postotni iznos) $y$ računamo na dva načina.

Prvi je način da razliku između nove vrijednosti $y$ i početne vrijednosti $x$ podijelimo s početnom vrijednošću i rješenje zapišemo u postotnom obliku.

Drugi je način da podijelimo novu vrijednost i početnu vrijednost, količnik napišemo u postotnom obliku te na kraju oduzmemo $100 %$ od tog postotka.

Porez na dodanu vrijednost

Kolekcija zadataka 2

Zadatak 9.

Maloprodajna cijena profesionalnog tostera je $750.00 kn .$ Budući da ga kupuje trgovina u kojoj se prodaju sendviči, platit će njegovu cijenu umanjenu za porez na dodanu vrijednost (PDV). Koliko će trgovina platiti toster?

Prisjetite se da je PDV $25 %$ i da se dodaje na osnovnu cijenu.

Zadatak možemo riješiti i s pomoću razmjera, koristeći se trojnim pravilom:

PDV se dodaje na osnovnu cijenu pa je postotak koji odgovara cijeni s PDV-om

$100 % + 25 % = 125 % .$

Cijeni bez PDV-a pritom odgovara postotak $100 % .$ Označimo tu cijenu s $x .$

Zapišemo razmjer $750 : x = 125 : 100 .$

Izračunamo nepoznati član razmjera, $x \cdot 125 = 750 \cdot 100.$

$125 x = 75 000$

$x = 75 000 : 125$

$x = 600 kn$

Cijena tog tostera bez PDV-a je $600 kn .$

Zadatak 10.

Cijena proizvoda bez PDV-a je $350 kn .$ Koliko će proizvod stajati s PDV-om?

Prisjetite se da je PDV $25 %$ i da se dodaje na osnovnu cijenu.

Cijena s PDV-om je

Cijenu upišite zaokruženu na dvije decimale.

$kn$ .

null

Zatvori

Zdravi život

Zanimljivost

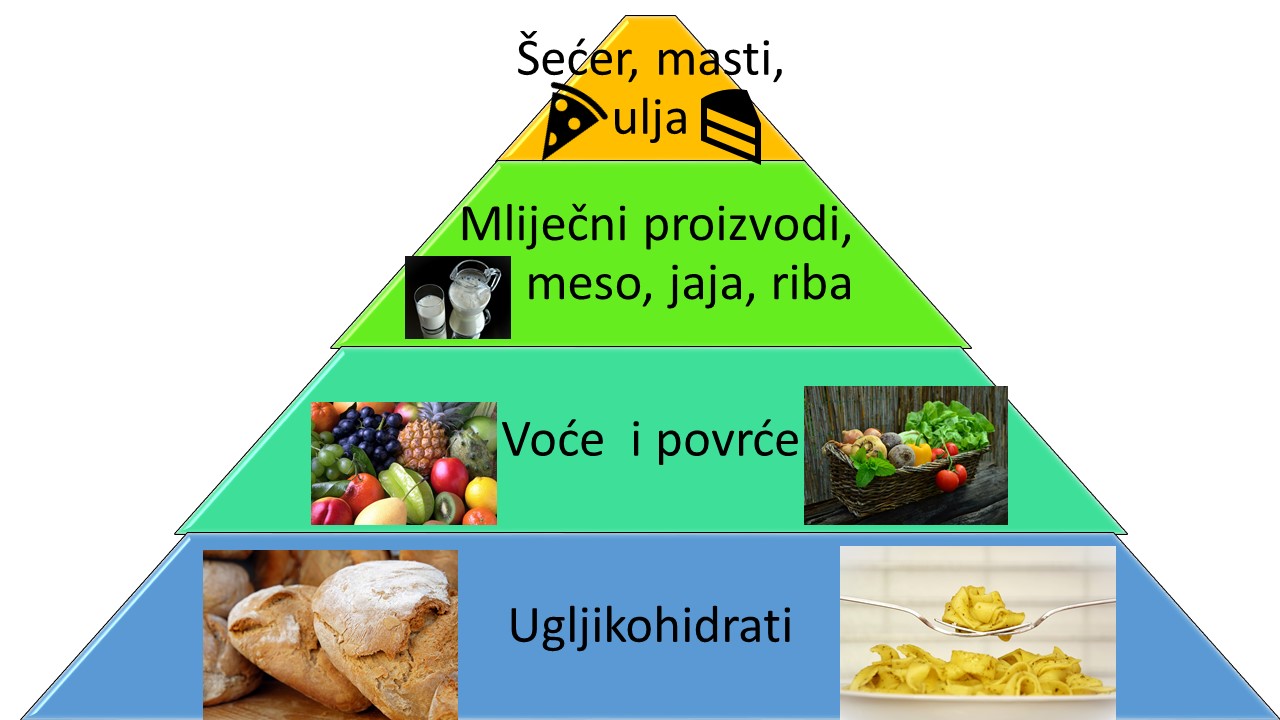
Piramida pravilne prehrane

Hrana koju jedemo mora odgovarati potrebama našega tijela za različitim hranjivim tvarima. Svrha piramide pravilne prehrane je pomoći ljudima u odabiru zdravih namirnica. Prehrana treba biti raznolika i umjerena. Temelj piramide su ugljikohidrati, na drugoj razini su voće i povrće, na trećoj mliječni proizvodi, meso, ribe i jaja, dok su na samom vrhu piramide šećer, masti i ulja te proizvodi koje treba konzumirati u najmanjoj količini.

Pročitajte više o piramidi pravilne prehrane na mrežnim stranicama OŠ Čavle.

Moderniju verziju piramide pravilne prehrane predstavilo je Američko ministarstvo poljoprivrede kako bi promicalo pravilnu prehranu i zdrave životne navike. Choose my plate (Moj tanjur) je alat koji su osmislili liječnici i nutricionisti. Njime je lakše pripremati svakodnevni jelovnik sa zdravim i raznovrsnim namirnicama. Izvor: Choose my plate, United States Department of Agriculture (engleski jezik).

Kolekcija zadataka 3

Zadatak 11.

U mlijeku ima $2.8 %$ mliječne masti. Koliki je obujam mliječne masti u $1 L$ takvog mlijeka?

U mlijeku od

$1 L$ je

Rješenje upišite brojčano. Prisjetite se da je

$1 L= 1 000 mL .$

$mL$ mliječne masti.

Pomoć:

$0.028 = 1 000$

null

Zadatak 12.

Ako $200 g$ peciva sa žitaricama ima $84 g$ ugljikohidrata, koliki je postotak ugljikohidrata u tom pecivu?

U tom je pecivu

Rezultat zapišite brojčano.

$%$ ugljikohidrata.

Pomoć:

$84 : 200$

null

Zatvori

Projekt

Sastavite jelovnik zdrave prehrane u kojem ćete iskoristiti postotke. Možete se poslužiti tablicom nutritivnih vrijednosti namirnica.

Zanimljivost

Važnost hidratacije organizma

Ljudska tkiva i kosti sadržavaju različite količine vode. Voda regulira tjelesnu temperaturu, olakšava gibanje zglobova, pomaže kruženju kemijskih spojeva, minerala, vitamina i hormona kroz tijelo, a njezinim izlučivanjem izbacuju se suvišne i štetne tvari iz organizma.

Unatoč tomu, ljudski organizam nema zalihe vode i soli. Njihove se količine stalno održavaju tako što bubrezi otpuštaju ili zadržavaju vodu i sol te reguliraju osjećaj žeđi.

Zato je važno svaki dan unositi dovoljno tekućine pijenjem i jedenjem namirnica koje sadržavaju vodu, kao što su voće i povrće. Ljudsko tijelo ima potrebu za $2.5 L$ vode na dan. Putem namirnica trebalo bi biti uneseno $20 %$ te količine, a $2 L$ izravnim pijenjem.

Izvor: Narodni zdravstveni list

Kolekcija zadataka 4

Zadatak 13.

Udjel vode u tijelu mlade osobe u prosjeku je $60 % .$ Marin je prema tome izračunao da $36 kg$ njegove mase otpada na vodu. Kolika je Marinova masa?

Marinova je masa

Odgovor upišite brojčano.

$kg .$

Pomoć:

$36 : 0.6$

null

Zadatak 14.

Kupnjom bicikla čija je cijena $2 640.00 kn,$ ostvarujete $12 %$ popusta na gotovinu.

Bicikl ćete, ako ga kupujete gotovinom, platiti

Rezultat upišite u obliku decimalnog broja s dvije decimale.

$kn .$

null

Zatvori

Zanimljivost

Slika prikazuje dio travnjaka u sjeni drveta. Bijeli ženski bicikl sa košarom je na travi

Vožnja biciklom odlična je za stjecanje kondicije, utječe na poboljšanje probave, izgara suvišne masnoće, povećava razinu energije za $20 %$ i smanjuje umor za $65 % .$ Bicikl je omiljeno prijevozno sredstvo u Danskoj, Nizozemskoj, Kini, Belgiji, Švicarskoj, Finskoj, Japanu i Norveškoj. Predlažemo da iskoristite svaku priliku za kretanje ili vožnju na svježem zraku.

Svijet oko nas

Kolekcija zadataka 5

Zadatak 15.

Slika prikazuje travu i na njoj glava konja. On pase travu.

Na stranici s popustima nudi se jahanje u Ekoselu, koje uz popust od $67 %$ stoji $198.00 kn .$ Kolika je cijena bez popusta?

Postotak koji odgovara sniženju je $33 % .$

$198 : 0.33 = 600 kn .$

Prije popusta, cijena jahanja bila je $600 kn .$

Zadatak 16.

Slika pokazuje infografiku Državnog zavoda za statistiku. Ona prikazuje statistiku slušanja glazbe na radiju. — Izvor slike: DZS

Pogledajte sliku pa odgovorite.

Koliko su sati trajale sve glazbene emisije 2015. godine?

$0.69 \cdot 1 113 663 = 768 427.47$ sati.

Sve glazbene emisije 2015. godine trajale su $768 427.47$ sati.

Zadatak 17.

U ožujku 2017. u komercijalnim smještajnim objektima najviše noćenja ostvareno je u Istarskoj županiji, i to $161 000$ noćenja. Najviše noćenja ostvarili su turisti iz Slovenije ( $22 %$ ). Koliko je slovenskih turista u tom vremenu noćilo u Istri?

Izvor: Turizam u ožujku 2017., Državni zavod za statistiku

$0.22 \cdot 161 000 = 35 420$ turista.

$35 420$ turista iz Slovenije ostvarilo je $22 %$ ukupnog broja noćenja u Istarskoj županiji u ožujku 2017. godine.

Zatvori

Kolekcija zadataka 6

Zadatak 18.

Na Zemlji ima $1 400 000 000 {km}^{3}$ vode. No samo $2.5 %$ vode je za piće.

Koliko je vode za piće na Zemlji?

Izvor: Geografija.hr

$0.025 \cdot 1 400 000 000 = 35 000 000 {km}^{3} .$

Na Zemlji je $35 000 000 {km}^{3}$ vode za piće.

Zadatak 19.

Slika prikazuje infografiku Državnog zavoda za statistiku. Na njoj je prikazan postotak učenici prvog razreda. — Izvor slike: DZS

Na kraju školske godine 2011./2012. bilo je u prvim razredima osnovnih škola $40 587$ učenika. U školskoj godini 2015./2016. bilo je $2.2 %$ prvašića više. Koliko je učenika bilo u prvim razredima te školske godine?

$2.2 %$ više, postotak koji odgovara povećanju je $102.2 % .$

$40 587 \cdot 1.022 \approx 41 480$ djece.

Riječ je o djeci pa rješenje zaokružimo na cijeli broj.

Te je godine bilo $41 480$ prvašića.

Zadatak 20.

Od $6.6$ milijardi stanovnika Zemlje, $88 %$ ih živi na sjevernoj polutki.

Koliko stanovnika živi na južnoj polutki?

Izvor: Enciklopedija.hr

Na južnoj polutki živi $12 %$ stanovnika. $0.12 \cdot 6 600 000 000 = 792 000 000 .$

Na južnoj polutki živi $792 000 000$ stanovnika.

Zatvori

Kutak za znatiželjne

Kolekcija zadataka 7

Zadatak 21.

Cijena $10$ -inčnog tableta bila je $780.00 kn .$ Ta je cijena najprije bila viša za $15 %,$ a zatim je snižena za $15 % .$ Koliko iznosi nova cijena?

Rješenje pogledajte u videozapisu Cijena $10$ -inčnog tableta.

Zadatak 22.

Cijena $1 L$ goriva bila je $8.00 kn .$ U prvom tjednu travnja cijena je viša za $20 %,$ a zatim je najavljeno sniženje od $20 % .$ Tata kaže da je dobro što će se cijena vratiti na staro. Ima li tata pravo? Kolika će biti nova cijena goriva?

Cijena goriva nakon povećanja od $20 %$ bila je $9.60 kn .$

Nova cijena goriva nakon sniženja od $20 %$ bila je $7.68 kn .$

Tata nema pravo. Nova cijena goriva nije jednaka staroj zato što se prvi postotak odnosi na cijenu od $8.00 kn,$ a drugi postotak na cijenu od $9.60 kn .$ Iako su postotci jednaki, osnovne vrijednosti na koje se odnose su različite.

Zadatak 23.

Cijena torbice od $700.00 kn$ snižena je $60 % .$ U istoj trgovini za gotovinsko plaćanje odobravaju popust od $5 % .$ Koliko će za torbicu izdvojiti djevojka koja torbicu plaća na sniženju gotovinom? Popusti se ne zbrajaju. Popust na gotovinsko plaćanje obračunava se na već sniženu cijenu.

Početna cijena torbice je: $x = 700 kn .$

Cijena torbice nakon sniženja je:

$y_{1} = 0.4 \cdot 700$

$y_{1} = 280 kn$

Na tu cijenu odobravaju još popust od $5 % .$

Cijena torbice s popustom za gotovinu je:

$y_{2} = 0.95 \cdot 280$

$y_{2} = 266 kn .$

Djevojka će torbicu platiti $266 kn .$

Zadatak 24.

Iznos koji treba izdvojiti za povratnu autobusnu kartu od Zadra do Osijeka je $396.00$ kuna. Za kartu djeteta do $12$ godina odobreno je $50 %$ popusta, a s karticom povjerenja autobusnog prijevoznika dodatnih $5 %$ popusta. Koliko treba izdvojiti za povratnu autobusnu kartu od Zadra do Osijeka za dijete?

$50 %$ od $396 kn$ je $198 kn .$ Popust od $5 %$ na taj iznos je $0.95 \cdot 198 = 188.10 kn .$

Za dječju povratnu kartu od Zadra do Osijeka treba izdvojiti $188.10 kn .$

Zatvori

Primjer 5.

Svježa jabuka sadržava $99 %$ vode, a sušena $9 % .$ Koliko ćemo čipsa od suhih jabuka dobiti od $182 kg$ svježih jabuka?

Rješenje pogledajte u videozapisu Čips od jabuka.

Zadatak 25.

Svježa marelica sadržava $92 %$ vode, a sušena $10 % .$ Koliko se kg sušenih marelica dobije od $112.5 kg$ svježih marelica?

U $112.5 kg$ svježih marelica ima $8 %$ suhe tvari, što je

$0.08 \cdot 112.5 = 9 kg .$

U osušenim marelicama također ima $9 kg$ suhe tvari, samo je to sada $90 %$ ukupne mase.

Izračunamo ukupnu masu, kao osnovnu vrijednost.

Možemo se koristiti razmjerom: $9 : x = 90 : 100,$ riješimo razmjer i dobijemo $x = 10 kg .$

Od $112.5 kg$ svježih marelica dobije se $10 kg$ sušenih marelica.

Projekt

Odaberite nekoliko različitih voćaka i izrežite ih na tanke ploške ili male komade. Izvažite ih i zapišite njihovu masu. Ostavite ih na prozračnome mjestu mjesec dana povremeno ih okrećući. Nakon mjesec dana opet izmjerite njihovu masu. Izvedite zaključak koliki je postotak mase voće izgubilo sušenjem.

Ako u vašoj okolici postoji sušara voća ili obiteljsko gospodarstvo koje se bavi sušenjem voća (primjerice smokvi, jabuka, šljiva), raspitajte se o njihovu postupku sušenja i saznajte koliki se postotak mase izgubi sušenjem.

Na početku...

Sniženje i poskupljenje

Zanimljivost

Zadatak 1.

Zadatak 2.

Kolekcija zadataka 1

Zadatak 3.

Zadatak 4.

Zadatak 5.

Zanimljivost

Zadatak 6.

Zadatak 7.

Zadatak 8.

Porez na dodanu vrijednost

Kolekcija zadataka 2

Zadatak 9.

Zadatak 10.

Zdravi život

Zanimljivost

Kolekcija zadataka 3

Zadatak 11.

Zadatak 12.

Projekt

Zanimljivost

Kolekcija zadataka 4

Zadatak 13.

Zadatak 14.

Zanimljivost

Svijet oko nas

Kolekcija zadataka 5

Zadatak 15.

Zadatak 16.

Zadatak 17.

Kolekcija zadataka 6

Zadatak 18.

Zadatak 19.

Zadatak 20.

Kutak za znatiželjne

Kolekcija zadataka 7

Zadatak 21.

Zadatak 22.

Zadatak 23.

Zadatak 24.

Zadatak 25.

Projekt

...i na kraju

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

3.6 Jednostavni kamatni račun