Matematika 7 - 7.2 Dijagonale mnogokuta

Na početku...

Sad kad smo dobro upoznali osnovne elemente svakog mnogokuta, možemo postupno početi proširivati svoje znanje. Svaki novi detalj koji naučimo otkrit će nam ljepotu geometrije.

Za početak pažljivo proučite sljedeće mnogokute.

Slika prikazuje tri mnogukuta s istaknutima dijagonalama: četverokut, dvadeseterokut i peterokut.

Nacrtanim mnogokutima plavom su bojom istaknute

Odgovor nije točan. :(

Pomoć:

Plavo su istaknute dužine koje spajaju dva nasuprotna vrha. Kako se zovu takve dužine?

null

Prebrojavanjem bismo vrlo jednostavno mogli odgovorili na pitanje koliko dijagonala imaju četverokut i peterokut, ali za dvadeseterokut - prebrojavati bi bilo izuzetno teško. Sasvim je prirodno upitati se: možemo li nekako izračunati taj broj?

Bilo bi divno kad bismo uspjeli otkriti vezu broja vrhova i broja dijagonala, osim one koja je očita: što je veći broj vrhova, bit će i više dijagonala.

Prije nego što počnemo s našim malim istraživanjem, prisjetimo se značenja pojma dijagonala.

Dijagonala mnogokuta je dužina koja spaja dva nesusjedna vrha mnogokuta.

Kolekcija zadataka 1

Zadatak 1.

Pažljivo pročitajte tekst i uparite odgovarajuće dijelove rečenica.

Dužina koja spaja susjedne vrhove mnogokuta naziva se
Dužina koja spaja nesusjedne vrhove mnogokuta naziva se

null

Zadatak 2.

Koliko susjednih vrhova ima svaki vrh mnogokuta?

jedan
Skicirajte bilo koji mnogokut, istaknite bilo koji vrh pa odgovorite na postavljeno pitanje. :)

dva
Točno. :)

ovisi o mnogokutu
Skicirajte bilo koji mnogokut, istaknite bilo koji vrh pa odgovorite na postavljeno pitanje. :)

null

null
Koliko nesusjednih vrhova ima svaki vrh mnogokuta?

jedan
Odgovor nije točan. Skicirajte barem tri različita mnogokuta, istaknite po jedan vrh svakome mnogokutu i prebrojite njemu nesusjedne vrhove. Razmislite još jedanput o odgovoru. :)

dva
Odgovor nije točan. Skicirajte barem tri različita mnogokuta, istaknite po jedan vrh svakome mnogokutu i prebrojite njemu nesusjedne vrhove. Razmislite još jedanput o odgovoru. :)

ovisi o mnogokutu
Točno. :)

null

null
Koliko se dijagonala može nacrtati iz jednog vrha mnogokuta?

jedna

dvije

ovisi o mnogokutu
Bravo!

null

null

Zatvori

Broj dijagonala iz jednog vrha

Zaključili smo da broj dijagonala iz jednog vrha ovisi o vrsti mnogokuta, odnosno o broju njegovih vrhova.

Možemo li uočiti neku pravilnost u međusobnoj vezi tih dvaju brojeva?

Istražimo.

Primjer 1.

Pokušajte uz pomoć GeoGebrine interakcije istražiti međusobni odnos i naći vezu između broja vrhova mnogokuta i broja dijagonala iz jednog vrha toga mnogokuta.

Pomicanjem klizača možete mijenjati broj vrhova mnogokuta, a odabirom vrha mnogokuta možete crtati ili brisati dijagonale iz tog vrha.

Dopunite tablicu i izvedite zaključak.

Provjerimo u sljedećim zadacima uspješnost našeg istraživanja i ispravnost izvedenog zaključka.

Zadatak 3.

Broj dijagonala koje se mogu nacrtati iz jednog vrha mnogokuta za $3$ je od broja vrhova (stranica, kutova) tog mnogokuta.

Pomoć:

Ima li mnogokut više vrhova ili dijagonala koje se mogu nacrtati iz jednog vrha?

null

Iz jednog vrha mnogokuta s $n$ vrhova može se nacrtati $n - 3$ dijagonale.

Dakle, ako neki mnogokut ima $n$ vrhova, tada svaki od njih ima $n - 3$ nesusjednih vrhova pa tako i $n - 3$ dijagonala koje se mogu iz njega nacrtati.

Pojasnimo. Potrebno je oduzeti upravo

3

(vrha) jer ne možemo nacrtati dijagonalu iz odabranog vrha do tog istog vrha niti možemo nacrtati dijagonale do njemu susjednih vrhova (to bi bile stranice mnogokuta).

Broj dijagonala iz jednog vrha, $d_{n}$

Mnogokut s $n$ vrhova ima $d_{n} = n - 3$ dijagonale iz jednog vrha.

Kolekcija zadataka 2

Zadatak 4.

Ako $n$ označava broj vrhova mnogokuta, a $d$ broj dijagonala koje se mogu nacrtati iz jednog vrha tog mnogokuta, spojite odgovarajuće parove.

$d = 5$	$n = 8$
$\begin{array}{l} n = 7 \end{array}$	$n = 15$
$d = 12$	$d = 4$
$n = 20$	$d = 17$

Pomoć:

Broj dijagonala iz jednog vrha uvijek je za $3$ manji od broja vrhova nekog mnogokuta. :)

null

Zadatak 5.

Koliko vrhova ima mnogokut ako se iz jednog njegova vrha može nacrtati ukupno $18$ dijagonala?

$21$
Bravo!

$15$
Netočno; broj vrhova mora biti za $3$ VEĆI od broja mogućih dijagonala iz jednog vrha.

Pomoć:

Prisjetite se veze broja vrhova nekog mnogokuta i broja dijagonala koje se mogu nacrtati iz jednog njegova vrha.

null
Koliko stranica ima $n$ -terokut kojemu se iz jednog vrha može nacrtati ukupno $8$ dijagonala?

$11$
Bravo!

$5$
Broj stranica isti je kao broj vrhova, dakle mora ih biti za $3$ više nego što ukupno ima dijagonala iz jednog vrha. :)

null
Ako neki mnogokut ima $13$ unutarnjih kutova, koliko se dijagonala može ukupno nacrtati iz jednog njegova vrha?

$16$
Broj unutarnjih kutova jednak je broju vrhova nekog mnogokuta pa on mora biti za $3$ veći od mogućeg broja dijagonala iz jednog njegova vrha.

$10$

null

Zatvori

Kolekcija zadataka 3

U sljedećim zadacima nemojte pogađati rješenja, nego uzmite papir i olovku, skicirajte i pokušajte riješiti zadatke. Ako ne uspijete riješiti iz prvog pokušaja, potražite pomoć klikom na odgovarajuću ikonu. :)

U rješavanju zadataka možete se koristiti danim predloškom.

Zadatak 6.

Barbara je nacrtala ukupno

6

dužina koje imaju zajedničku početnu točku. Kako se zove mnogokut koji je počela crtati? Barbara crta .

Ilustracija prikazuje djevojčicu koja je nacrtala 6 dužina sa zajedničkom početnom točkom.

Pomoć:

Skicirajte na papir (ili na predložak) Barbarin crtež. Dvije od nacrtanih dužina su stranice, a preostale $4$ su dijagonale iz jednog vrha.

Postupak:

Barbara je nacrtala $6$ dužina koje su istaknute plavom bojom. U smjeru suprotnom od kazaljke sata imenujte preostale vrhove i docrtajte stranice mnogokuta.

Slika prikazuje sedmerokut, rješenje zadatka.

Zadatak 7.

Bruno je nacrtao $6$ dužina sa zajedničkom početnom točkom koja je vrh (budućeg) mnogokuta. Nacrtane dužine predstavljaju dijagonale mnogokuta iz vrha $A .$

Ako ovaj mnogokut ima $6$ dijagonala iz jednog vrha, tada mora imati
Skicirajte na papir zadani crtež. Prisjetite se u kojem su odnosu broj dijagonala nacrtanih iz jednog vrha i broj vrhova mnogokuta.
vrhova.

Pomoć:

Prisjetite se u kojem su odnosu broj dijagonala nacrtanih iz jednog vrha i broj vrhova mnogokuta.

Postupak:

Broj vrhova nekog mnogokuta za tri je veći od ukupnog broja dijagonala nacrtanih iz jednog njegova vrha.
Da bi crtež bio ispravan, potrebno je docrtati
Ako ima $6$ dijagonala iz vrha $A,$ znači da vrh $A$ ima $6$ nesusjednih vrhova. Mora imati još i $2$ susjedna (koja se trebaju docrtati).
vrha.

Pomoć:

Ako ima $6$ dijagonala iz vrha $A,$ znači da vrh $A$ ima $6$ nesusjednih vrhova. Mora imati još i $2$ susjedna (koja se trebaju docrtati).

Postupak:

Vrh $A (1),$ njemu nesusjedni vrhovi $(6)$ i susjedni vrhovi $(2) .$ Ukupno je to $9$ vrhova.

Zatvori

Ukupan broj dijagonala mnogokuta

Možemo li sada izračunati ukupan broj dijagonala mnogokutima iz uvodnog primjera?

Sljedeći primjer pomoći će vam u traženju odgovora na postavljeno pitanje.

Primjer 2.

Uz pomoć interaktivnog uratka istražite vezu broja vrhova mnogokuta i ukupnog broja dijagonala toga mnogokuta.

Možemo li izračunati ukupni broj dijagonala ako znamo broj vrhova mnogokuta?

Klizačem možete mijenjati broj vrhova mnogokuta, odabirom gumba Dijagonale možete pratiti animaciju, a gumb Pomoć ostavite za trenutak kad vam ponestane ideja.

Provjerimo zaključke istraživanja:
Neki $n$ -terokut ima vrhova. Iz svakog njegova vrha može se nacrtati dijagonale.

Pomoć:

Ponovo proučite aplet u prethodnom primjeru.
Ukupni broj dijagonala mnogokuta s $n$ vrhova računamo:

$n \cdot (n - 3)$

$\frac{n \cdot (n - 3)}{2}$

Pomoć:

Još jedanput proučite prethodni primjer i usporedite ga s ponuđenim odgovorom.

Zadatak 8.

Izračunajte ukupan broj dijagonala peterokuta i provjerite rješenje prebrojavanjem dijagonala. (U odgovoru upišite brojke.) Peterokut ima ukupno dijagonala.

null

Slika prikazuje peterokut s istaknutim dijagonalama.

Peterokut ima $5$ vrhova, iz svakog vrha izlaze $2$ dijagonale $(5 - 3) .$ Ukupan broj dijagonala dobit ćemo ako pomnožimo broj vrhova s brojem dijagonala iz jednog vrha (umnožak je $10$ ) te podijelimo s dva, jer smo svaku dijagonalu brojili $2$ puta.

Dakle, postoji ukupno $5$ dijagonala, a to lako možemo provjeriti prebrojavanjem.

Ako mnogokut nema puno vrhova, odnosno - ako je $n$ neki jednoznamenkasti broj, račun najčešće izvodimo napamet. Međutim, katkad nam neće biti jednostavno množiti, a zatim i dijeliti napamet pa je preporučljivije račun zapisati.

Želimo li matematičkim jezikom zapisati izraz koji će nam dati ukupan broj dijagonala nekog $n$ -terokuta, učinit ćemo to na sljedeći način:

Ukupni broj dijagonala mnogokuta, $D_{n}$

Mnogokut s $n$ vrhova ukupno ima $D_{n} = \frac{n \cdot (n - 3)}{2}$ dijagonala.

Zadatak 9.

Slika prikazuje dvadeseterokut sa svim dijagonalama

Sada smo spremni odgovoriti na pitanje iz uvodnog dijela.
Koliko ukupno dijagonala ima dvadeseterokut? Dvadeseterokutu se ukupno može nacrtati (upišite broj) dijagonala.

Pomoć:

Kako računamo ukupni broj dijagonala nekog mnogokuta?

Koliko ima dijagonala iz jednog vrha mnogokuta?

Možda će biti jednostavnije ako zapišete postupak. :)

Postupak:

$n = 20$

Iz jednog vrha mnogokuta možemo povući $17$ dijagonala ( $n - 3$ ) pa je ukupni broj dijagonala

$D_{20} = \frac{20 \cdot 17}{2}$

U ovom je slučaju jednostavnije skratiti $20$ i $2,$ nego najprije množiti faktore u brojniku.

Nakon skraćivanja, rješenje lako možemo izračunati i napamet.

Izračunajte i provjerite točnost upisivanjem broja na predviđeno mjesto.

$\underline{n = 20}$

D_{n} = ?

D_{n} = \frac{n (n - 3)}{2}

$D_{n} = \frac{20 (20 - 3)}{2}$

$D_{n} = \frac{20 \cdot 17}{2}$

$D_{n} = 10 \cdot 17$

$D_{n} = 170$

Primjer 3.

Koliko vrhova ima mnogokut koji ima ukupno $9$ dijagonala?

$\underline{D_{n} = 9}$

$n = ?$

Umjesto oznake za ukupan broj dijagonala, napisat ćemo formulu te izjednačiti s $9 :$

$\frac{n (n - 3)}{2} = 9$
Pomnožimo cijelu jednadžbu s $2$ kako bi nam ostao izraz iz brojnika lijeve strane:

$n$ $(n - 3)$ $= 18$

Sada umnožak broja $n$ s brojem koji je za $3$ manji od njega daje $18 .$

Povremeno možemo napamet otkriti takva dva broja, ali ako ne uspijemo (a nećemo uspjeti uvijek), najsigurnije nam je rastaviti taj umnožak na proste faktore.

Dakle, $18 = 2 \cdot 3 \cdot 3$

Sada možemo uočiti da prva dva faktora daju umožak $6,$ a preostane nam $3 .$

$18 = 6 \cdot 3$

Pronašli smo takva dva prirodna broja koji se razlikuju za $3,$ a pomnoženi daju $18 .$

Veći od tih faktora je broj stranica mnogokuta ( $n$ ), a manji je broj dijagonala iz jednog vrha.

U našem primjeru, $n = 6,$ dakle radi se o šesterokutu.

Zadatak 10.

Koji mnogokut ima ukupno

20

dijagonala?

Primijenite postupak rješavanja iz prethodnog primjera. :)

Pomoć:

Zadan je ukupan broj dijagonala, $D_{n} = 20,$ a traži se $n .$

Uz pomoć postupka opisanog u rješenju prethodnog primjera, pokušajte točno odgovoriti.

null

Primjer 4.

Postoji li mnogokut kojemu se ukupno može nacrtati $77$ dijagonala?

U ovom je zadatku ponovo poznat ukupan broj dijagonala:

$\underline{D_{n} = 77}$

ali je postavljeno pitanje: postoji li mnogokut?

Pitamo se: zašto ne bi postojao? Kakav bi to trebao biti $n$ (broj vrhova) da mnogokut ne postoji.

Naravno, broj $n$ mora biti prirodni broj (jer ne može mnogokut imati npr. $4.5$ vrhova), i to veći od broja $2$ (jer je trokut mnogokut s najmanjim brojem stranica).

Dakle,

$n = ?$ $\Leftrightarrow$ Saznamo li $n$ $\in$ $N,$ $n \geq 3,$ moći ćemo reći koji je to mnogokut.

Kao i u prethodnom primjeru, umjesto oznake $D_{n},$ napisat ćemo formulu te izjednačiti sa $77 .$ Nakon toga pomnožit ćemo cijelu jednadžbu s $2$ kako bi nam ostao izraz iz brojnika lijeve strane:

$n (n - 3) = 154$

Tražimo takva dva prirodna broja koji se razlikuju za $3,$ a umnožak im je $154 .$

To će teže ići napamet, stoga rastavimo taj umnožak na proste faktore.

Dakle, $154 = 2 \cdot 77 = 2 \cdot 7 \cdot 11$

Uočavamo da kombinacija $14 \cdot 11$ zadovoljava tražene uvjete, iz čega slijedi da je $n = 14 .$

Dakle, traženi mnogokut je četrnaesterokut.

Kolekcija zadataka 4

Zadatak 11.

Postoji li mnogokut koji ima $12$ dijagonala?

$\underline{D_{n} = 12}$

$\begin{array}{l} n = ? \end{array}$ $\begin{array}{l} \Leftrightarrow \end{array}$ Saznamo li $n,$ moći ćemo reći koji je to mnogokut.

Kao i u prethodnom primjeru, umjesto oznake $\begin{array}{l} D_{n} \end{array}$ napisat ćemo formulu te izjednačiti s $12 .$ Nakon toga, pomnožit ćemo cijelu jednadžbu s $2$ kako bi nam ostao izraz iz brojnika lijeve strane:

$n (\begin{array}{l} n - 3 \end{array}) = 24$

Tražimo takva dva prirodna broja koji se razlikuju za $3,$ a pomnoženi daju $24 .$

Rastavimo taj umnožak na proste faktore.

Dakle, $24 = 2 \cdot 2 \cdot 2 \cdot 3$

Možemo dobiti sljedeće kombinacije: $4 \cdot 6$ ili $8 \cdot 3$ ili $12 \cdot 2,$ ali ni jedan od parova brojeva ne zadovoljava uvjet da je jedan faktor za $3$ veći od drugoga.

S obzirom na to da ne postoji takav $n,$ zaključujemo da ni mnogokut s $12$ dijagonala ne postoji.

Zadatak 12.

Za sljedeći zadatak nije dovoljno samo odgovoriti na pitanje. Važan je postupak rješavanja, uz razumijevanje napisanoga, naravno.

Postoji li mnogokut kojemu se može nacrtati ukupno:

$10$ dijagonala?

Da.

Ne.

Pomoć:

Iskoristite postupak iz rješenja prethodnog primjera. :)

null
$65$ dijagonala?

Da.

Ne.

null

Zatvori

Primjer 5.

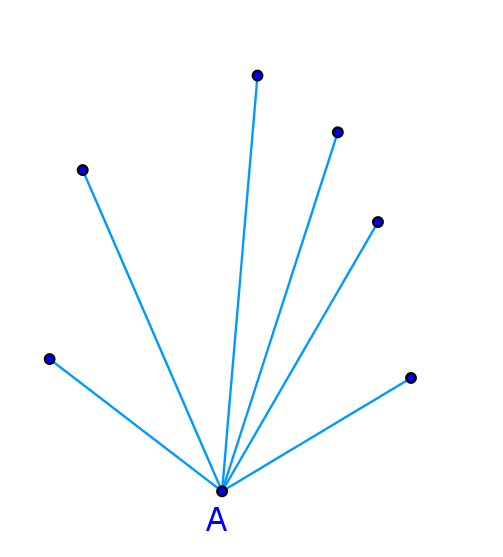
Ekipe sedam vinkovačkih osnovnih škola sudjeluju na turniru u odbojci. Koliko će utakmica biti odigrano ako svaka ekipa mora odigrati po jednu utakmicu sa svakom preostalom ekipom?

Možemo zamisliti da je svaka ekipa vrh mnogokuta.

Ako svaka ekipa igra sa svakom, broj utakmica bit će jednak broju svih dužina na crtežu, a to su sve dijagonale i sve stranice mnogokuta, tj. $D_{n} + n .$

Budući da znamo da je $n = 7,$ možemo lako izračunati $D_{n} = 14 .$

Zaključujemo da će se odigrati $21$ utakmica.

Zadatak 13.

Pred kinom se srelo $8$ prijatelja. Ako se svaki rukovao sa svakim, koliko je bilo rukovanja?

20

28

8

Pomoć:

Prijatelje možete prikazati kao vrhove osmerokuta. Rukovanja su dužine koje povezuju vrhove, a to su sve dijagonale i same stranice mnogokuta.

Postupak:

Postupak rješavanja potražite u rješenju prethodnog primjera. Jedina razlika je u broju vrhova.

7.2 Dijagonale mnogokuta

Na početku...

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Broj dijagonala iz jednog vrha

Zadatak 3.

Kolekcija zadataka 2

Zadatak 4.

Zadatak 5.

Kolekcija zadataka 3

Zadatak 6.

Zadatak 7.

Ukupan broj dijagonala mnogokuta

Zadatak 8.

Zadatak 9.

Zadatak 10.

Kolekcija zadataka 4

Zadatak 11.

Zadatak 12.

Zadatak 13.

Uvježbajmo!

Kolekcija zadataka 5

Zadatak 14.

Zadatak 15.

Zadatak 16.

Zadatak 17.

Zanimljivost

Kolekcija zadataka 6

Zadatak 18.

Zadatak 19.

Zadatak 20.

...i na kraju

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

7.3 Kutovi mnogokuta