Matematika 7 - 4.3 Relativna frekvencija i aritmetička sredina

Boja automobila	Broj automobila
plava	$2$
crvena	$7$
srebrna	$4$
crna	$6$
bijela	$3$

Frekvencija

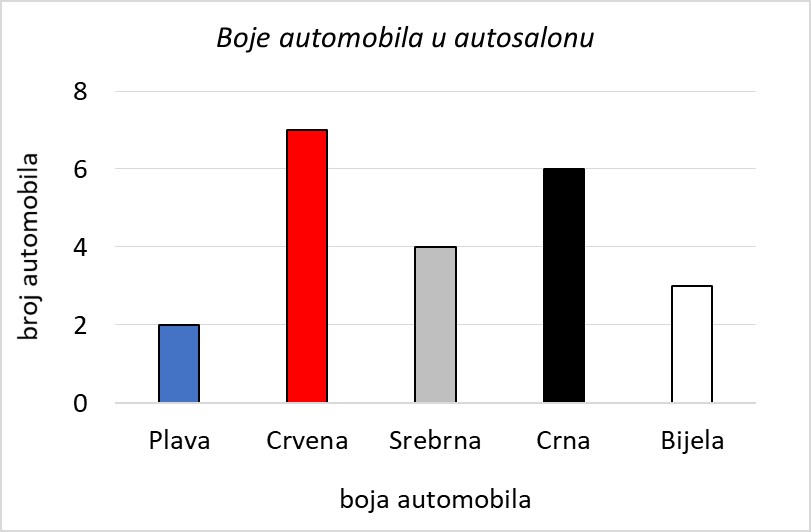
Skup objekata ovdje su automobili, njihovo obilježje koje promatramo je boja automobila. Vrijednosti tog obilježja su plava, crvena, srebrna, crna i bijela.

Broj pojavljivanja određene boje, primjerice crvene, naziva se frekvencija ili učestalost.

Iz tablice vidimo da je frekvencija crvene boje automobila broj $7 .$ Frekvencija plave boje automobila je $2 .$

Tablicu u kojoj su zapisane frekvencije obično nazivamo tablica frekvencija.

Ukupan broj pojavljivanja je zbroj svih frekvencija, tj. ovdje je to ukupan broj automobila, broj $22 .$

Frekvencija ili učestalost neke vrijednosti je broj koji nam kazuje koliko se puta ta vrijednost pojavila u nekom skupu podataka.

Primjer 1.

Učenici jednoga sedmog razreda razgovaraju o knjigama koje su pročitali tijekom praznika. Jedna djevojčica pročitala je knjigu Čudesne zvijeri i gdje ih naći, šestero učenika pročitalo je Tajni dnevnik Adriana Molea, osmero je pročitalo Kronike iz Narnije, troje Sportski život Letećeg Martina, dvoje Dobri duh Zagreba, a jedan je dječak pročitao Malog princa. Nacrtajmo u bilježnicu tablicu frekvencija za taj skup podataka.

Naslov knjige	Broj učenika, frekvencija
Čudesne zvijeri i gdje ih naći	$1$
Tajni dnevnik Adriana Molea	$6$
Kronike iz Narnije	$8$
Sportski život Letećeg Martina	$3$
Dobri duh Zagreba	$2$
Mali princ	$1$

Zadatak 1.

Adrian je spremao ormar i otkrio da ima $7$ crvenih majica, $5$ plavih, $6$ žutih, $12$ bijelih i $4$ zelene majice. Nacrtajmo u bilježnicu tablicu frekvencija za taj skup podataka.

Boja majice	Broj majica, frekvencija
crvena	$7$
plava	$5$
žuta	$6$
bijela	$12$
zelena	$4$

Stupčasti dijagram koji možemo nacrtati iz tablice frekvencija nazivamo stupčasti dijagram frekvencija.

Stupčasti dijagrami koje ste crtali u prethodnoj jedinici također su bili stupčasti dijagrami frekvencija.

Zanimljivost

Zadatke koje treba razvrstati u tablicu i nacrtati dijagram možete riješiti i u jednom od alata spomenutih u prethodnim jedinicama. Primjerice, dijagrame možete nacrtati s pomoću MS Excela i na taj način uštedjeti vrijeme potrebno za računanje i crtanje.

Primjer 2.

Vlasnici slastičarnice provode istraživanje o vrstama kolača koje posjetitelji najviše vole. Zapisivali su narudžbe u jednom danu i došli do sljedećih podataka. Kremšnite su naručila $23$ posjetitelja, čokoladnu tortu $17$ posjetitelja, tortu od sira $14$ posjetitelja, voćne košarice $15$ posjetitelja, punč-kocke $7$ posjetitelja i ostale kolače $10$ posjetitelja. Nacrtajmo u bilježnicu tablicu frekvencija i pripadni stupčasti dijagram frekvencija za to istraživanje.

Na slici je tablica i dijagram frekvencija za istraživanje prodaje kolača u slastičarnici

Zanimljivost

na slici je vodoravni stupčasti (trakasti) dijagram istraživanja prodaje kolača u slastičarnici

U stupčastom dijagramu obilježje stavljamo na os $x,$ a frekvenciju na os $y .$ Kod vodoravnog stupčastog dijagrama je obrnuto.

Kolekcija zadataka 1

Zadatak 2.

Na jednom je kiosku prodavačica zapisivala prodaju dnevnih novina tijekom jednog jutra. Došla je do podataka da je prodano $16$ primjeraka Jutarnjeg lista, $12$ primjeraka Večernjeg lista, $36$ primjeraka $24$ sata, $8$ primjeraka Slobodne Dalmacije i $12$ primjeraka Glasa Slavonije. Nacrtajte u bilježnicu tablicu frekvencija i pripadni stupčasti dijagram frekvencija za te podatke.

Tablica frekvencija

Dnevne novine	Broj prodanih primjeraka, frekvencija
Jutarnji list	$16$
Večernji list	$12$
$24$ sata	$36$
Slobodna Dalmacija	$8$
Glas Slavonije	$12$

Na slici je stupčasti dijagram koji prikazuje prodaju naših dnevnih novina u kiosku — Stupčasti dijagram frekvencija

Zadatak 3.

U 7. b razredu učenici su odlučili ići na sedmodnevnu ekskurziju. No nisu bili jednoglasni u dogovoru o odredištu. Naime, $7$ je učenika željelo ići u Pulu, $3$ u Makarsku, $4$ u Vodice, $8$ u Dubrovnik, a $3$ u Crikvenicu.

Nacrtajte u bilježnicu tablicu frekvencija i pripadni stupčasti dijagram frekvencija za odredišta ekskurzije.

Tablica frekvencija

Destinacija	Broj učenika, frekvencija
Pula	$7$
Makarska	$3$
Vodice	$4$
Dubrovnik	$8$
Crikvenica	$3$

Na slici je stupčasti dijagram frekvencija izbora destinacije za ekskurziju — Stupčasti dijagram frekvencija

Zatvori

Relativne frekvencije

Zanima nas udjel promatrane frekvencije neke vrijednosti u odnosu prema ukupnom broju pojavljivanja.

Zadatak 4.

U 7. a razredu $6$ je učenika iz Njemačkog jezika dobilo ocjenu odličan, u 7. b razredu ocjenu odličan dobila su $4$ učenika, a u 7. c $5$ učenika. Možemo li zaključiti da je 7. a razred najuspješniji u njemačkom jeziku? O odgovoru na to pitanje raspravite u razredu i zajedno pronađite rješenje.

Iz navedenih podataka ne možemo zaključiti da je 7. a razred najuspješniji u njemačkom jeziku. Naime, iako je veći broj učenika dobio odličnu ocjenu, možda taj razred ima i najviše učenika u uspredbi s ostalim razredima. Potrebno je promotriti broj učenika koji su dobili odličnu ocjenu u usporedbi s ukupnim brojem učenika u razredu.

Primjer 3.

Ocjene na ispitu znanja iz Hrvatskog jezika u jednome sedmom razredu prikazane su u tablici frekvencija.

Za svaku ocjenu izračunajmo udjel njezine učestalosti u usporedbi s ukupnim brojem svih ocjena.

Ocjena Frekvencija

nedovoljan ( $1$ ) $2$

dovoljan ( $2$ ) $4$

dobar ( $3$ ) $8$

vrlo dobar ( $4$ ) $6$

odličan ( $5$ ) $5$

Ocjena	Frekvencija
nedovoljan ( $1$ )	$2$
dovoljan ( $2$ )	$4$
dobar ( $3$ )	$8$
vrlo dobar ( $4$ )	$6$
odličan ( $5$ )	$5$

Ukupan broj svih ocjena je $24,$ a dobili smo ga zbrajajući sve frekvencije.

Udjel frekvencije za ocjenu nedovoljan u odnosu prema ukupnom broju je $2 : 25 = 0.08 .$
Udjel frekvencije za ocjenu dovoljan u odnosu prema ukupnom broju je $4 : 25 = 0.16 .$
Udjel frekvencije za ocjenu dobar u odnosu prema ukupnom broju je $8 : 25 = 0.32 .$
Udjel frekvencije za ocjenu vrlo dobar u odnosu prema ukupnom broju je $6 : 25 = 0.24 .$
Udjel frekvencije za ocjenu odličan u odnosu prema ukupnom broju je $5 : 25 = 0.2 .$
Udjel frekvencije u odnosu prema ukupnom broju podataka nazivamo relativna frekvencija.

Relativna frekvencija je udjel frekvencije neke vrijednosti u odnosu prema ukupnom broju promatranih podataka.

Zadatak 5.

Istraživanje je pokazalo da učenici i studenti sve više traže dodatne poduke iz mnogih predmeta. Tako su iz Matematike na dodatnu poduku u jednu udrugu protekle godine redovito dolazili učenici osnovne škole, učenici srednje škole i studenti s fakulteta. Raspodjela je prikazana u tablici.

Skupina	Frekvencija
osnovna škola	$150$
srednja škola	$270$
fakultet	$80$

Za svaku skupinu izračunajte udjel učestalosti (relativnu frekvenciju).

Na dodatne poduke iz Matematike dolazilo je
Pozorno pročitajte zadatak.
osoba.

Pomoć:

Odgovor napišite u numeričkom obliku na za to predviđeno mjesto.

null
Relativna frekvencija za skupinu učenika iz osnovne škole koji uzimaju dodatne poduke je
Pozorno pročitajte zadatak.
.

Pomoć:

Rezultat upišite u obliku decimalnog broja s jednom decimalom na za to predviđeno mjesto.

null
Relativna frekvencija za skupinu učenika iz srednje škole koji uzimaju dodatne poduke je
Pozorno pročitajte zadatak.
.

Pomoć:

Rješenje upišite u obliku decimalnog broja s dvije decimale na za to predviđeno mjesto.

null
Relativna frekvencija za skupinu studenata s fakulteta koji uzimaju dodatne poduke je
Pozorno pročitajte zadatak.
.

Pomoć:

Rješenje upišite u obliku decimalnog broja s dvije decimale na za to predviđeno mjesto.

null

Za relativne frekvencije računamo udjel u odnosu prema cijelini pa je relativna frekvencija uvijek broj veći od $0$ i manji od $1$ .

Zbrojimo sve relativne frekvencije iz primjera.

$0.08 + 0.16 + 0.32 + 0.24 + 0.2 = 1$

Zbroj reativnih frekvencija nekog skupa podataka uvijek mora biti $1 .$

Ako želimo pregledno prikazati podatke, u tablicu frekvencija dodamo stupac s relativnim frekvencijama.

Primjer 4.

$18$ učenika natječe se u skoku udalj. Rezultati su zapisani redom kako su učenici skakali: $4.2 m,$ $4.1 m,$ $4.2 m$ , $4.5 m,$ $4.3 m,$ $4.3 m$ , $4.1 m$ , $4.2 m$ , $4.5 m$ , $4.7 m,$ $4.4 m,$ $4.3 m$ , $4.3 m$ , $4.1 m$ , $4.4 m$ , $4.4 m$ , $4.3 m$ i $4.2 m$ .
Prikažite u bilježnicu rezultate tablicom frekvencija i relativnih frekvencija.

Ukupan broj natjecatelja je $18 .$ Relativnu frekvenciju pojedine duljine skoka dobijemo tako da frekvenciju te duljine podijelimo s $18 .$ Relativne frekvencije možemo pisati u obliku razlomka ili decimalnog broja zaokruženog na dvije ili tri decimale. Zbroj relativnih frekvencija uvijek mora biti $1 .$ Katkad, zbog zaokruživanja decimalnih brojeva relativnih frekvencija, zbroj neće biti točno $1$ nego približno, kao u ovom primjeru.

Duljina skoka	Frekvencija	Relativna frekvencija (razlomci)	Relativna frekvencija
$4.1 m$	$3$	$\frac{3}{18}$	$0.17$
$4.2 m$	$4$	$\frac{4}{18}$	$0.22$
$4.3 m$	$5$	$\frac{5}{18}$	$0.28$
$4.4 m$	$3$	$\frac{3}{18}$	$0.17$
$4.5 m$	$2$	$\frac{2}{18}$	$0.11$
$4.7 m$	$1$	$\frac{1}{18}$	$0.06$
Zbroj	$18$		$1$

Zadatak 6.

U jednome dalmatinskome mjestu upisivali su imena stanovnika. Opazili su da se ime Marija pojavljuje $27$ puta, Ivan $23$ puta, Lucija $12$ puta, Ante $14$ puta, Kate $4$ puta i Lovre $20$ puta. Prikažite u bilježnicu rezultate tablicom frekvencija i relativnih frekvencija.

Ime	Frekvencija	Relativna frekvencija (decimalni brojevi)	Relativna frekvencija (razlomci)	Relativna frekvencija (postotci)
Marija	$27$	$0.27$	$\frac{27}{100}$	$27 %$
Ivan	$23$	$0.23$	$\frac{23}{100}$	$23 %$
Lucija	$12$	$0.12$	$\frac{12}{100}$	$12 %$
Ante	$14$	$0.14$	$\frac{14}{100}$	$14 %$
Kate	$4$	$0.04$	$\frac{4}{100}$	$4 %$
Lovre	$20$	$0.2$	$\frac{20}{100}$	$20 %$
Zbroj	$100$	$1$		$100 %$

Relativna frekvencija uvijek je broj između $0$ i $1$ pa se može izraziti u obliku postotka. Prisjetimo se da je cjelina $100 %$ i da je $100 % = 1 .$ Ukupan zbroj svih relativnih frekvencija zapisanih u obliku postotka mora biti $100 % .$

Relativnu frekvenciju zapisanu u obliku postotka nazivamo i postotak učestalosti.

Zanimljivost

Posjetite mrežnu stranicu DZS-a, Imena i prezimena u Republici Hrvatskoj pa pogledajte koliko imenjaka i prezimenjaka imate. Izračunajte postotak učestalosti svojeg imena u cijeloj hrvatskoj populaciji.

Na popisu 2011. zabilježeno je da je u Republici Hrvatskoj bilo $4 284 889$ osoba, od toga $2 218 554$ žena i $2 066 335$ muškaraca.

Na spomenutoj mrežnoj stranici saznali smo da osoba s imenom Lidija ima $9 689,$ postotak učestalosti među ukupnom populacijom je $9 689 : 4 284 889 = 0.00226 = 0.226 %,$ a ako pogledamo postotak učestalosti imena Lidija među ženama, dobivamo $9 689 : 2 218 554 = 0.00437 = 0.437 % .$

Znatno veći postotak učestalosti imaju imena Marija i Ivan.

Marija = $126 646 : 4 284 889 = 2.956 %$

Ivan = $130 828 : 4 284 889 = 3.053 %$

Primjer 5.

U trgovini elektroničkom opremom provode istraživanje tjedne prodaje. Mobitela je prodano $17,$ tableta $11,$ prijenosnih računala $20,$ stolnih računala $13,$ igraćih konzola $30$ te ostalih proizvoda $104 .$

Prikažite rezultate u bilježnicu tablicom frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.

Ukupan broj prodanih elektroničkih proizvoda tijekom tog tjedna je $195 .$ Relativnu frekvenciju pojedinog proizvoda dobijemo tako da frekvenciju tog proizvoda podijelimo sa $195 .$ Relativne frekvencije u obliku postotka dobijemo tako da dobiveni decimalni broj pomnožimo sa $100 .$ Zbroj relativnih frekvencija uvijek mora biti $1 .$ Zbroj relativnih frekvencija u obliku postotka uvijek mora biti $100 % .$ Katkad, zbog zaokruživanja decimalnih brojeva relativnih frekvencija, zbroj postotaka neće biti točno $100 %$ nego približno.

Proizvod elektroničke opreme	Frekvencija	Relativna frekvencija (decimalni brojevi)	Relativna frekvencija u obliku postotka
mobitel	$17$	$0.09$	$9 %$
tablet	$11$	$0.06$	$6 %$
prijenosno računalo	$20$	$0.10$	$10 %$
stolno računalo	$13$	$0.07$	$7 %$
igraća konzola	$30$	$0.15$	$15 %$
ostali proizvodi	$104$	$0.53$	$53 %$
zbroj	$195$	$1$	$100 %$

Zadatak 7.

U 7. d razredu učenici su proveli istraživanje o tome što najviše vole raditi tijekom slobodnog vremena. Sedmero učenika izjavilo je da voli svirati, dvanaestero učenika bavi se sportom, dvoje učenika voli igrati računalne igrice ili gledati TV, a četvero učenika voli slobodno vrijeme provoditi u prirodi.

Prikažite rezultate u bilježnicu tablicom frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.

Aktivnost	Frekvencija	Relativna frekvencija	Relativna frekvencija u obliku postotka
glazba	$7$	$0.28$	$28 %$
sport	$12$	$0.48$	$48 %$
igrice i TV	$2$	$0.08$	$8 %$
priroda	$4$	$0.16$	$16 %$
zbroj	$25$	$1$	$100 %$

Aritmetička sredina

Za brojčane podatke koje smo razvrstali u tablicu frekvencija često nas zanima i prosječna vrijednost, sredina. Primjerice, zanimaju nas prosječna ocjena, prosječna plaća, prosječna potrošnja goriva, prosječna brzina, prosječna temperatura... U matematici se ta prosječna vrijednost ili sredina naziva aritmetička sredina.

Primjer 6.

U jednoj manjoj tvrtki djelatnici su redom dobili sljedeće iznose plaća: $5 604 kn,$ $5 832 kn,$ $7 200 kn,$ $7 220 kn,$ $7 534 kn$ i $10 201 kn .$

Pogledajte niz podataka o plaćama pa razmislite koja bi mogla biti aritmetička sredina plaća?

Iznos aritmetičke sredine plaće mogao bi biti bilo koji iznos između najniže i najviše plaće u toj tvrtki i vjerojatno nije nijedan od navedenih iznosa plaća. Da bismo saznali prosječnu vrijednost plaće u toj tvrtki, moramo izračunati aritmetičku sredinu svih iznosa plaća djelatnika te tvrtke.

Aritmetička sredina niza brojčanih podataka je broj koji označava srednju ili prosječnu vrijednost.

Aritmetička sredina ne mora biti jednaka ni jednoj brojčanoj vrijednosti niza podataka od kojih računamo prosječnu vrijednost. Aritmetička vrijednost mora biti između najmanje i najveće brojčane vrijednosti skupa podataka.

Zadatak 8.

Razmislite i odgovorite.

Visine petorice prijatelja su $175 cm,$ $177 cm,$ $180 cm$ i dvojica najviših visoka su $181 cm .$ Je li neki od tih podataka prosječna visina petorice prijatelja?

Pažljivo pročitajte pitanje, razmislite ili pogledajte uputu.

Pomoć:

Prosječna visina petorice prijatelja je $178.8 cm,$ što ne vidimo iz ovih podataka nego moramo izračunati.

null

Što mislite, kako bismo mogli odrediti koliki je iznos prosječne plaće tvrtke iz primjera ili kolika je prosječna visina petorice prijatelja iz zadatka?

Moramo izračunati aritmetičku sredinu skupa brojčanih podataka. To ćemo učiniti tako da zbrojimo sve podatke i dobiveni zbroj podijelimo s ukupnim brojem zadanih podataka.

Aritmetičku sredinu označavamo s $\bar{x}$ .

Primjer 7.

Koristeći se podatcima iz primjera s plaćama djelatnika tvrtke i zadatka s visinama petorice prijatelja, izračunajmo:

aritmetičku sredinu svih plaća tvrtke iz primjera

prosječnu visinu petorice prijatelja iz zadatka.

Zbroj iznosa svih plaća je $43 591 kn .$ Djelatnika je $6 .$ Podijelimo $43 591$ sa $6$ i dobit ćemo iznos prosječne plaće.

$43 591 : 6 = 7 265.17 kn,$ zaokruženo na dvije decimale

Aritmetička sredina uobičajeno se zaokružuje na dvije decimale.

Prosječna plaća zaposlenika u toj tvrtki je $7 265.17 kn,$ i nijedan djelatnik nema točno taj iznos plaće. Zamijetili smo da samo dvoje zaposlenika ima plaću veću od prosječne, a četvero ih ima plaću manju od prosječne plaće u toj tvrtki.
Zbroj visina prijatelja je $894 cm .$ Prijatelja je $5,$ pa podijelimo $894$ s $5 .$

$894 : 5 = 178.8 cm .$ Prosječna visina petorice prijatelja je $178.8 cm .$

Dvojica su niža od prosječne visine, a trojica viša od prosječne visine tih petorice prijatelja.

Zanimljivost

U videozapisu DZS-a Male škole statistike "Medijan i prosjek" pojavljuje se još jedan pojam, medijan, koji je važan statistički pokazatelj. Više o medijanima i statistici općenito učit ćete u srednjoj školi ili na fakultetu.

Aritmetičku sredinu niza brojčanih podataka računamo tako da podatke zbrojimo i podijelimo s ukupnim brojem zadanih podataka.

$\bar{x} = \frac{x_{1} + x_{2} + . . . + x_{n}}{n},$ gdje su $x_{1}, x_{2}, . . . x_{n}$ zadani brojčani podatci, a $n$ ukupan broj podataka.

Možemo pisati i $\bar{x} = (x_{1} + x_{2} + . . . + x_{n}) : n .$

Zadatak 9.

Šestorica prijatelja usporedila su brojeve cipela. Njihovi su brojevi cipela: $36,$ $38,$ $39,$ $42,$ $42$ i $43 cm .$ Koji je prosječni broj cipela šestorice prijatelja?

Prosječni broj cipela šestorice prijatelja je

Pažljivo pročitajte zadatak.

Pomoć:

Pri rješavanju zadatka zbrojite sve brojeve cipela. Zbroj podijelite brojem prijatelja čije brojeve cipela smo uzimali. Koristite se formulom za izračunavanje aritmetičke sredine.

Rezultat upišite u obliku cijelog broja na za to predviđeno mjesto.

null

Primjer 8.

Učenici sedmog razreda pisali su ispit znanja iz Povijesti. Učitelj im je donio ispite na uvid, ali prije toga rekao je da su bile tri nedovoljne ocjene, jedna dovoljna, pet dobrih, sedam vrlo dobrih i pet odličnih. Kolika je prosječna ocjena tog razreda na provedenom ispitu znanja?

Budući da ocjena ima previše da bismo ih sve pojedinačno zapisivali u formulu, a neke se ocjene ponavljaju, možemo ih grupirati kao što je to učinio učitelj. Izbrojit ćemo koliko ima kojih ocjena pa brojčanu vrijednost ocjene pomnožiti s ukupnim brojem pojavljivanja te ocjene. Zatim ćemo te umnoške zbrojiti te ćemo tako dobiti ukupan zbroj svih ocjena. Taj ćemo zbroj podijeliti s ukupnim brojem ocjena i dobiti prosječnu ocjenu koju su postigli učenici tog razreda na ispitu znanja. Računski bi to izgledalo ovako:

$\bar{x} = \frac{3 \cdot 1 + 1 \cdot 2 + 5 \cdot 3 + 7 \cdot 4 + 5 \cdot 5}{21}$

$\bar{x} = \frac{73}{21},$ rješenje zaokružimo na dvije decimale

$\bar{x} \approx 3.48.$

Prosječna ocjena razreda na ispitu znanja iz Povijesti je dobar ( $3.48$ ).

Kolekcija zadataka 2

Zadatak 10.

Učenice 7. a i 7. b razreda natječu se u skoku udalj. Duljine njihovih skokova su $3.6 m,$ $3.9 m,$ $3.6 m,$ $4.2 m,$ $4.2 m$ , $4.1 m,$ $3.8 m,$ $4.3 m,$ $4.1 m$ , $4.3 m$ , $4.1 m$ , $3.6 m$ , $4.5 m,$ $4.1 m$ , $4.2 m$ , $3.8 m$ , $4.3 m$ , $3.6 m$ , $4.2 m$ , $3.6 m$ i $3.9 m$ . Kolika je prosječna duljina njihovih skokova?

Prosječna duljina njihovih skokova je

m .

Pomoć:

Kako biste riješili zadatak, grupirajte pa zbrojite udaljenosti koje su učenice postigle skokom. Zbroj udaljenosti podijelite brojem učenica. Rezultat zapišite u brojčanom obliku na za to predviđeno mjesto.

Postupak:

$\frac{3.6 \cdot 5 + 3.8 \cdot 2 + 3.9 \cdot 2 + 4.1 \cdot 4 + 4.2 \cdot 4 + 4.3 \cdot 3 + 4.5 \cdot 1}{21} = 4$

Zadatak 11.

Lunin račun za telefon iznosio je $200 kn$ prva $3$ mjeseca, zatim se povećao na $234 kn$ sljedeća $4$ mjeseca, a nakon toga spustio na $180 kn$ sljedećih $5$ mjeseci. Koliki je bio prosječni Lunin telefonski račun protekle godine?

Lunin prosječni telefonski račun protekle godine bio je

Pažljivo pročitajte zadatak.

kn .

Pomoć:

Pomnožite broj mjeseci za koje je jednak iznos na računu tim iznosom, potom zbrojite sve rezultate. Krajnji rezultat podijelite brojem mjeseci u godini, odnosno brojem mjeseci čije smo račune uzimali u obzir (12 mjeseci).

null

Zatvori

Kutak za znatiželjne

Sljedeći primjeri i zadatci matematički su malo zahtjevniji, ali ih možete svi pokušati riješiti. Kad ih riješite, međusobno usporedite rješenja i postupke te pomozite prijateljima koji su zastali u rješavanju zadatka.

Primjer 9.

Filipa želi iz Fizike imati odličan uspjeh, a zasad ima ove ocjene: usmeno $4$ i $5$ , pismeno $5$ i $5,$ vježbe i praktičan rad $4,$ $5$ i $5 .$ Koju najmanju ocjenu može dobiti iz radne bilježnice a da joj prosjek još bude za odličan uspjeh, tj. najmanje $4.5 ?$

Ako Filipa želi imati odličan uspjeh iz Fizike, mora imati prosjek ocjena najmanje $4.5$ . S ocjenom iz radne bilježnice imat će ukupno $8$ ocjena. Prosjek ocjena je aritmetička sredina svih ocjena pa zapišimo formulu aritmetičke sredine $\bar{x} = \frac{x_{1} + x_{2} + . . . + x_{n}}{n} .$ Nepoznatu ocjenu označimo s $x$ i uvrstimo podatke.

$4.5 = \frac{4 + 5 + 5 + 5 + 4 + 5 + 5 + x}{8}$ riješimo linearnu jednadžbu s jednom nepoznanicom

$4.5 = \frac{33 + x}{8}$ $/ \cdot 8$

$33 + x = 36$

$x = 3 .$

Najmanja ocjena koju Filipa može dobiti iz radne bilježnice je $3 .$

Zadatak 12.

Marijeta je odlučila štedjeti za novi bicikl. Prvi je mjesec uštedjela $234 kn,$ drugi $340 kn,$ treći $270 kn,$ a četvrti $120 kn .$ Ako uspije uštedjeti prosječno $220 kn$ u prvih $5$ mjeseci, ostatak iznosa koji je potrebno izdvojiti za bicikl podmirit će majka. Koliki iznos Marijeta treba uštedjeti $5 .$ mjesec.

Marijeta mora uštedjeti

Pažljivo pročitajte zadatak.

kn .

Pomoć:

Zbrojite sve iznose koje je Marijeta uštedjela tijekom 4 mjeseca. Kako bi prosječni iznos trebao iznositi $220 kn,$ pomnožite $220$ s $5 .$ Od toga broja oduzmite zbroj iznosa za prva $4$ mjeseca.

Rezultat zapišite u obliku cijelog broja na za to predviđeno mjesto.

Postupak:

$220 \cdot 5 - (234 + 340 + 270 + 120) = 1 100 - 964 = 136$

Projekt

Izmjerite svoju visinu i visine svojih prijatelja te izračunajte prosječnu visinu. U bilježnicu zapišite visine u tablicu, izradite tablicu frekvencija. Izračunajte relativne frekvencije i relativne frekvencije u obliku postotka. Zbrojite sve relativne frekvencije i relativne frekvencije u obliku postotka.

Frekvencija ili učestalost neke vrijednosti je

Ponovite ovu jedinicu.

koji nam kaže koliko se puta ta vrijednost pojavila u nekom skupu podataka.

null

Udjel frekvencije neke vrijednosti u odnosu prema ukupnom broju promatranih podataka naziva se

Pozorno pročitajte zadatak.

Pomoć:

Odgovor upišite u obliku dviju riječi odvojenih razmakom na za to predviđeno mjesto.

null

Aquapark na jednoj plaži nudi ulaznice u nekoliko cjenovnih kategorija. Imaju posebnu cijenu za djecu, odrasle, cjelodnevnu ulaznicu, ali i obiteljske pakete. Tablicom je prikazana frekvencija prodaje pojedinih ulaznica.

Vrsta ulaznice	Frekvencija
djeca	$64$
odrasli	$46$
cjelodnevna ulaznica	$28$
obiteljski paket	$62$

Ukupno je prodano

Pozorno pročitajte zadatak.

ulaznica.

Relativna frekvencija ulaznica za djecu je

Pozorno pročitajte zadatak.

Relativna frekvencija ulaznica za odrasle je

Pozorno pročitajte zadatak.

Relativna frekvencija cjelodnevnih ulaznica je

Pozorno pročitajte zadatak.

Relativna frekvencija obiteljskog paketa ulaznica je

Pozorno pročitajte zadatak.

Pomoć:

Ukupan broj ulaznica izračunat ćete tako da zbrojite sve ulaznice. Odgovor upišite u obliku cijelog broja na za to predviđeno mjesto.

Relativnu frekvenciju pojedine grupe ulaznica izračunat ćete tako da podijelite broj određene grupe ulaznica s ukupnim brojem ulaznica. Odgovor upišite u obliku decimalnog broja s dvjema decimalama na za to predviđeno mjesto. Taj broj mora biti između $0$ i $1 .$

null

Anita je u jednoj računalnoj igrici postigla ove bodove:

121,

129,

239,

345,

12

273 .

Koliki je prosječan broj bodova koje je Anita postigla? Prosječan broj bodova koje je Anita postigla je

Pozorno pročitajte zadatak.

bodova.

Pomoć:

Odgovor upišite u obliku decimalnog broja s jednom decimalom na za to predviđeno mjesto.

null

Tea je u siječnju zaradila

2 345 kn,

u veljači

2 765 kn,

ožujku

3 000 kn

i u travnju

3 212 kn .

Tea je u ta četiri mjeseca prosječno zaradila

Pozorno pročitajte zadatak.

kn .

Pomoć:

Odgovor upišite u obliku decimalnog broja s dvjema decimalama na za to predviđeno mjesto.

null

ZAVRŠITE PROCJENU

4.3 Relativna frekvencija i aritmetička sredina

Na početku...

Frekvencija

Zadatak 1.

Zanimljivost

Zanimljivost

Kolekcija zadataka 1

Zadatak 2.

Zadatak 3.

Relativne frekvencije

Zadatak 4.

Zadatak 5.

Zadatak 6.

Zanimljivost

Zadatak 7.

Aritmetička sredina

Zadatak 8.

Zanimljivost

Zadatak 9.

Kolekcija zadataka 2

Zadatak 10.

Zadatak 11.

Kutak za znatiželjne

Zadatak 12.

Projekt

...i na kraju

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

4.4 Analiza podataka