Početna veličina slova
Kojih oblika ima najviše na slici?
Kad se osvrnete oko sebe, vidite li koji predmet kružnog oblika?
Nabrojite sve predmete kružnog oblika koje vidite oko sebe.
Prisjetite se nekog kružnog oblika iz prirode.
Raširite ruke i zavrtite se oko svoje osi. Što su opisale vaše ruke?
Pomoć:
Ako niste sigurni u odgovor, zavrtite se još jedanput.
Da biste nacrtali kružnicu, trebate jednu točku u sredini i duljinu dužine od te točke do rubnih točaka.
Pomoć:
Latice cvijeta podsjećaju na jednake udaljenosti od točke u sredini do ruba.
Pripremite pribadaču, konopac i olovku.
Jedan kraj konopca pribadačom stisnite uz papir, a u drugi kraj stavite olovku i kružite olovkom oko pribadače. Što ste dobili?
Kružnica je skup svih točaka ravnine jednako udaljenih od neke čvrste točke te ravnine.
Kako se zove točka ravnine oko koje opisujemo kružnicu?
Središte kružnice je točka u ravnini od koje su jednako udaljene sve točke kružnice.
Kružnice crtamo ručno šestarom ili uz pomoć digitalnih alata u programima dinamičke geometrije kao što su GeoGebra i The Geometer's Sketchpad.
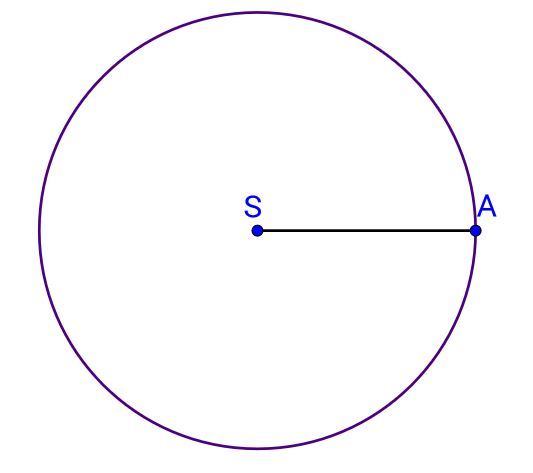
Da bismo nacrtali kružnicu, trebamo označiti središte kružnice
i trebamo znati udaljenost točaka kružnice od točke
Dužinu koja spaja središte i neku točku na kružnici nazivamo radijus ili polumjer kružnice.
Duljinu te dužine također nazivamo radijus ili polumjer i označavamo
Kružnica oko središta S polumjera rMatematička oznaka za kružnicu sa središtem u točki polumjera je Oznaku čitamo "kružnica sa središtem polumjera ".
Spojite parove.
| ( ) | |
| ( ) | |
| ( ) | |
| ( ) |
Pomoć:
Veliko slovo u zagradi označava središte kružnice, broj s mjernom jedinicom označava duljinu polumjera kružnice.
Primjer 1.
Konstruirajmo kružnicu ( ).
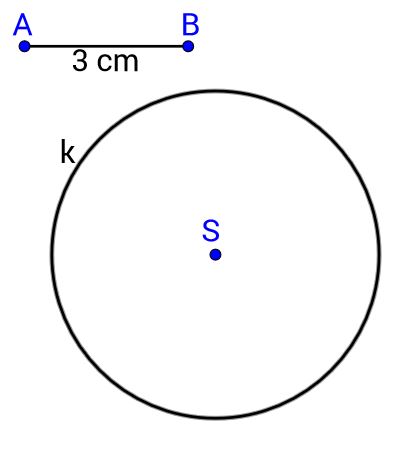
U ravnini odaberemo bilo gdje točku i nacrtamo dužinu duljine Uzmemo u šestar duljinu dužine šestar zabodemo u točku i oko točke opišemo kružnicu
U bilježnicu nacrtajte kružnicu u ravnini. Zatim nacrtajte dužinu koja spaja dvije točke na kružnici i prolazi središtem kružnice.
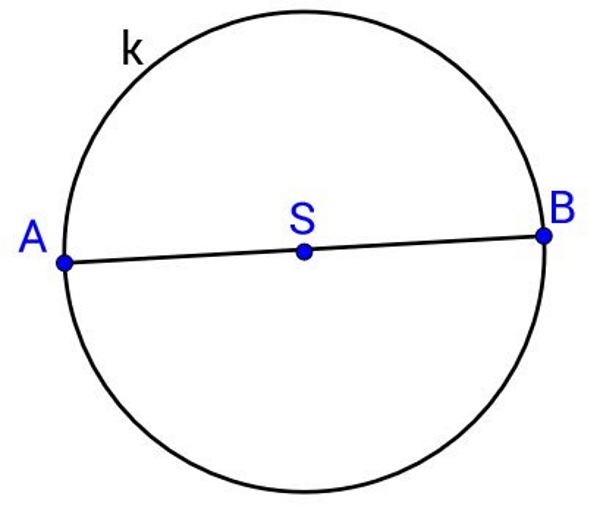
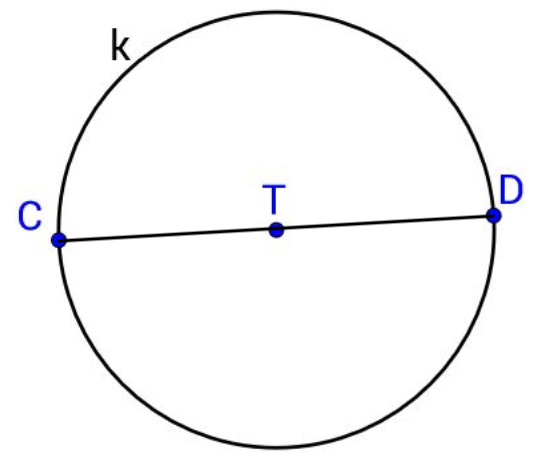
Dužinu koja spaja dvije točke na kružnici i prolazi središtem kružnice nazivamo dijametar ili promjer kružnice.
Označimo krajnje točke promjera s i Duljinu te dužine također nazivamo dijametar ili promjer i označavamo
Uobičajena oznaka u svakodnevnom životu za promjer je slovo koje se čita "fi" i dolazi iz grčkog alfabeta. Slovo izgledom podsjeća na kružnicu i njezin promjer pa se zato baš to slovo upotrebljava za oznaku u svakodnevnom životu. U matematici se češće koristi latinično slovo što dolazi od riječi dijametar.
Krajnje točke promjera nazivamo dijametralno suprotne točke.
Spojite parove.
|
|
dijametralno suprotne točke |
|
Točke
i
|
središte kružnice |
|
Točka
|
polumjer kružnice |
|
|
promjer kružnice |
Pomoć:
Pažljivo pogledajte sliku.
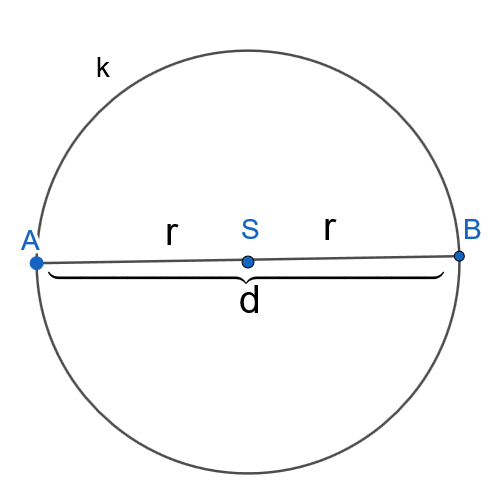
Promjer je dva puta dulji od polumjera Pišemo
Primjer 2.
Izračunajmo duljinu polumjera kružnice promjera
Ako je promjer dva puta dulji od polumjera, onda je polumjer dva puta kraći od promjera, pa duljinu promjera treba podijeliti s
Primjer 3.
Konstruirajmo kružnicu promjera
Nacrtajmo u bilježnicu
=
Konstruirajmo njezino polovište.
Ako ste zaboravili kako se konstruira polovište dužine, pogledajte GeoGebrinu interakciju.
Prvo nacrtajte zadanu dužinu, zatim uzmite u šestar malo više od pola duljine te dužine i nacrtajte dijelove kružnice iz krajnjih točaka dužine. Kroz sjecišta lukova povucite pravac. Točka u kojoj pravac siječe dužinu je polovište te dužine.
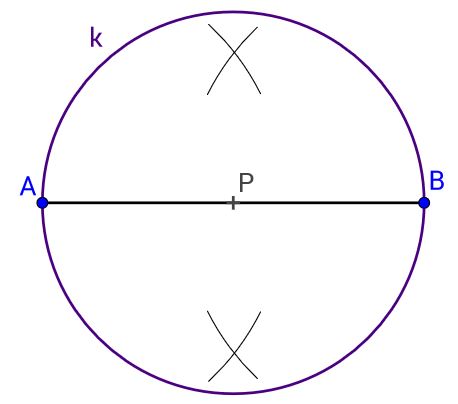
U polovište dužine zabodimo šestar, odmjerimo do jedne i druge dijametralno suprotne točke i i nacrtajmo kružnicu oko točke
Konstruirajte u bilježnicu kružnicu promjera
Krug je dio ravnine omeđen kružnicom.
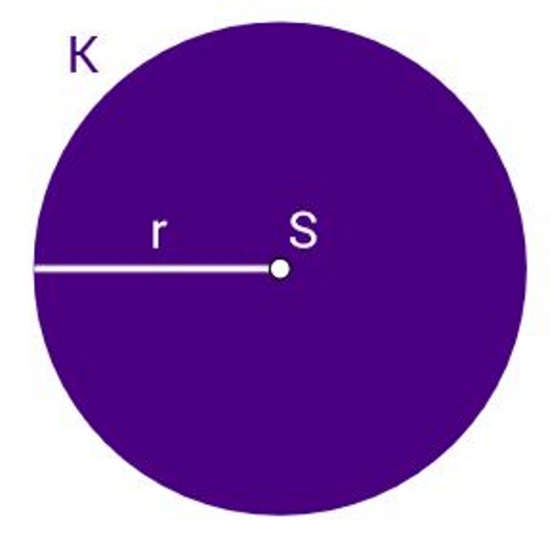
Krug sa središtem u točki
polumjera
matematički označavamo
i čitamo "krug sa središtem u točki
polumjera
".
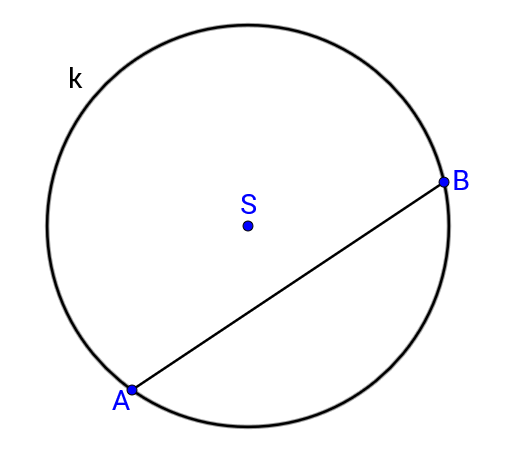
Dužinu koja spaja dvije točke na kružnici nazivamo tetiva.
Nacrtajte u bilježnicu kružnicu ( ). Nacrtajte njezinu najdulju tetivu. Što primjećujete?
Dio kružnice omeđen dvjema točkama na toj kružnici nazivamo kružni luk.
Matematička oznaka za kružni luk omeđen točkama
i
kružnice je
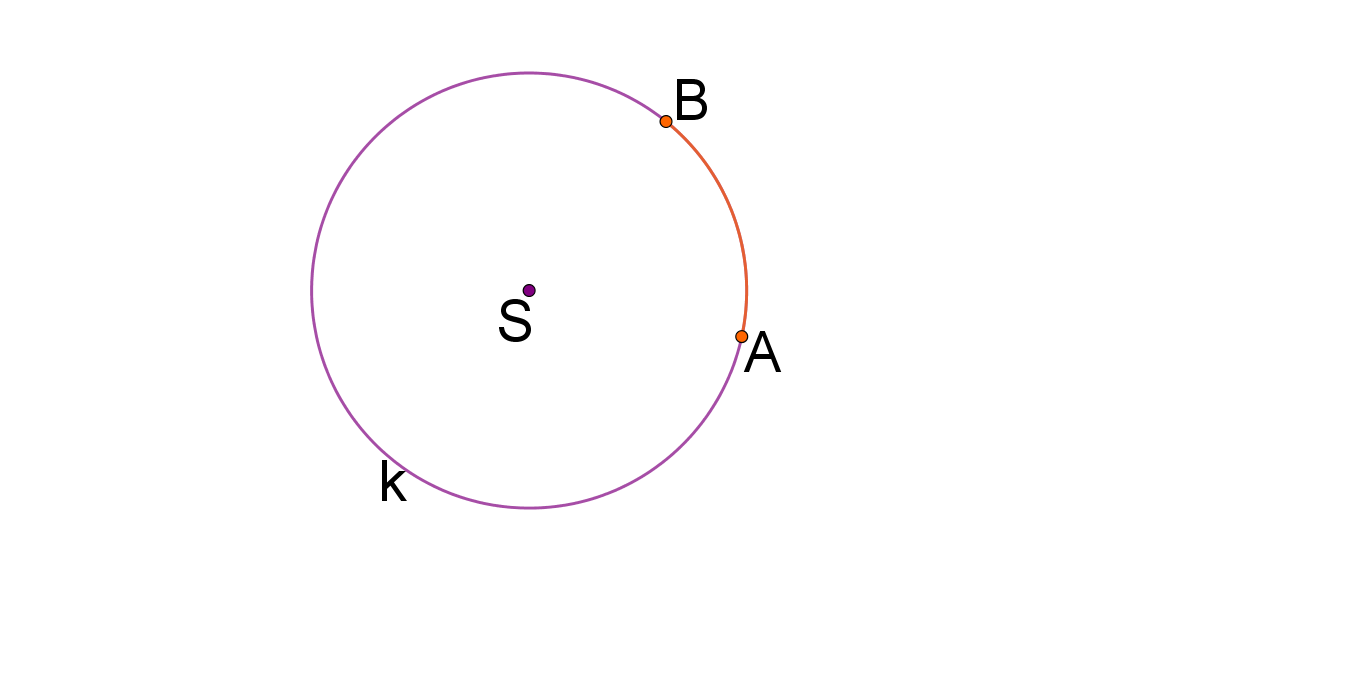
Pravilno čitanje kružnog luka sa slike je obrnuto od kazaljke na satu. Tako je kružni luk sa slike manji kružni luk, a kružni luk veći kružni luk. Kad crtate kružne lukove u nekoj od dinamičkih geometrija, morate na to pripaziti, ali kad crtate kružne lukove u bilježnicu, uobičajeno se misli na manji kružni luk, osim ako ne piše drugačije u zadatku, pa se ne mora toliko paziti na to koju ćete točku napisati prvu.
Na slici je isječen komad sira iz koluta kružnog oblika.
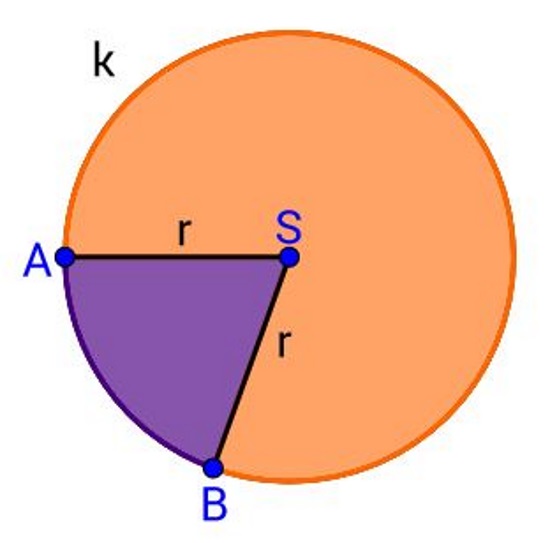
Dio kruga omeđen dvama polumjerima toga kruga i pripadnim kružnim lukom nazivamo kružni isječak.
Na slici je odsječen komad kruha od kruha kružnog oblika.
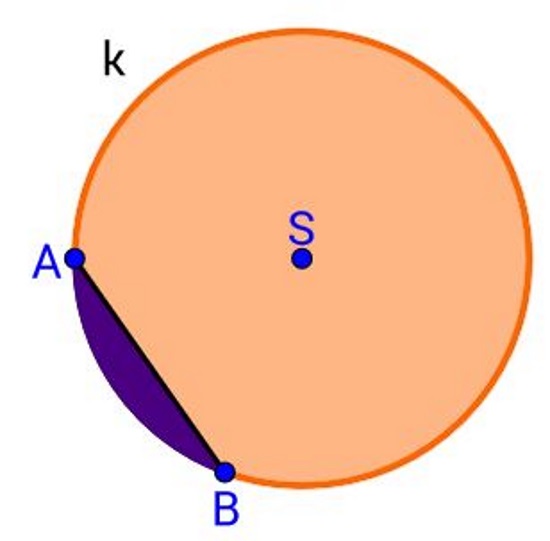
Dio kruga omeđen jednom tetivom toga kruga i pripadnim kružnim lukom nazivamo kružni odsječak.
Što je zajedničko kružnicama na slici?
Nacrtajte
u bilježnicu
tri kružnice oko iste točke
(
),
(
) i
(
).
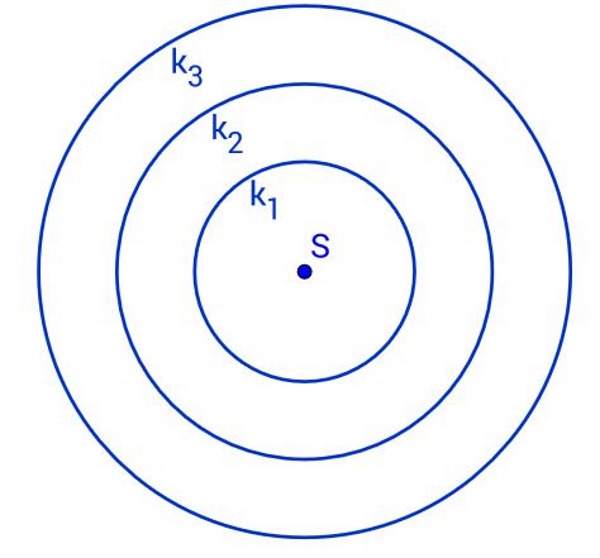
Kružnice u istoj ravnini koje imaju zajedničko središte nazivamo koncentrične kružnice.
Što se nalazi na vratima ograde?
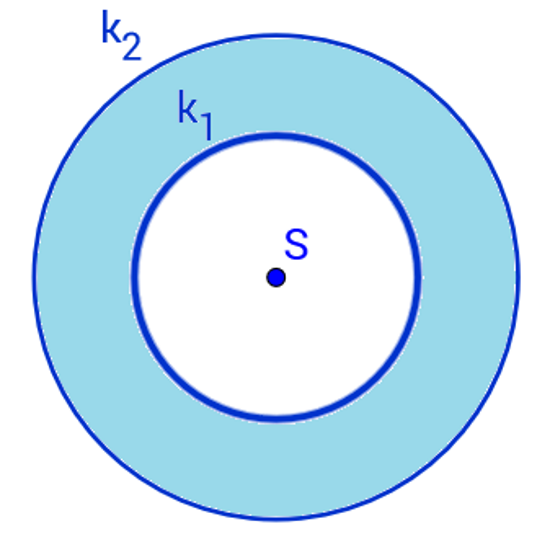
Dio ravnine omeđen dvjema koncentričnim kružnicama nazivamo kružni vijenac.
Kružnica i krug na slici podijeljeni su na dva jednaka dijela.
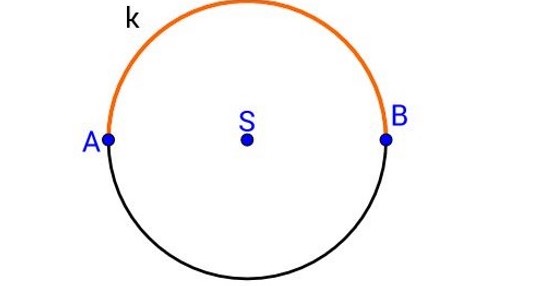
Dio kružnice između dviju dijametralno suprotnih točaka nazivamo polukružnica.
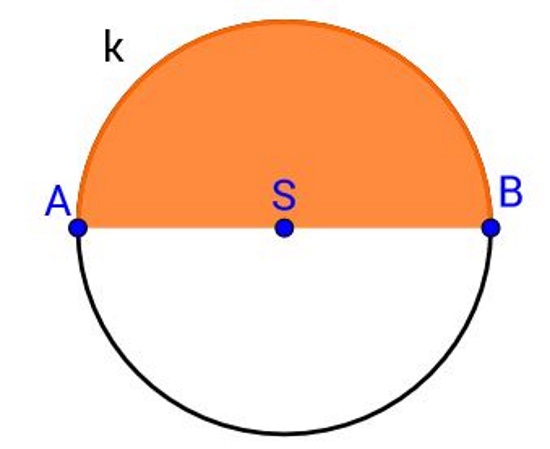
Dio kruga omeđen jednim promjerom i pripadnom polukružnicom nazivamo polukrug.
Ponovite dijelove kruga i kružnice u sljedećoj igrici. Bodove skupljate tako da kliknete na sliku elementa čiji se naziv pojavi u dnu ekrana. Pokušajte dobiti najveći broj bodova. Ako krivo kliknete pomicanje se ubrzava. Imate tri pokušaja za svaki element.
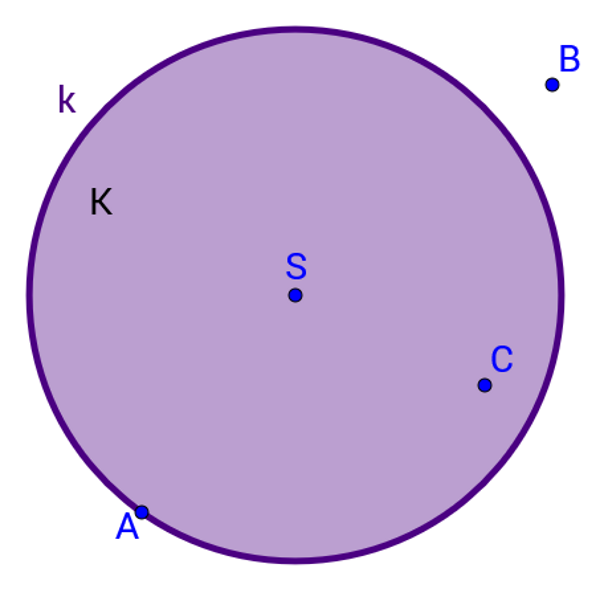
Koje su izjave točne?
Pomoć:
Razmislite što znači da točka pripada nekom skupu točaka.
Koje dijelove kružnice vidite na slici?
Pomoć:
Traže se dijelovi kružnice, ne dijelovi kruga.
Polukrug je ujedno i kružni isječak i kružni odsječak.
Pomoć:
Omeđen je dvama polumjerima, koji čine promjer, i pripadnim kružnim lukom - polukružnicom.
Omeđen je najduljom tetivom i pripadnim kružnim lukom.
"Ne dirajte moje krugove" - bile su, prema legendi, posljednje riječi velikoga grčkog matematičara i fizičara starog vijeka Arhimeda iz Sirakuze. U vrijeme opsade Sirakuze, dok je Arhimed crtao u pijesku krugove i proučavao ih, prišao mu je rimski vojnik. Arhimed ga je upozorio da ne dira njegove krugove. Vojnik ga je ubio jer je smatrao da Arhimed tom rečenicom vrijeđa moć pobjednika. Na nadgrobnoj ploči Arhimedova groba nalaze se kugla i valjak u čast njegova znanstvenog rada.
U ovoj jedinici naučili ste ili ponovili kružnicu i krug i njihove elemente i dijelove. Vidjeli ste slike s kružnim oblicima. Krug nalazimo na mnogo mjesta u prirodi. Kružni oblici koriste se svugdje. Najvažniji čovjekov izum kružnog oblika je kotač. Možete li zamisliti život bez kotača?
Kotač nije važan samo u prometu, nego i za radne strojeve, jer omogućava neki rad uz manju silu. Prijenos energije omogućen je zupčanicima, remenicom ili koloturom. Kotač upotrebljavamo i za iskorištavanje vodene energije (mlinsko kolo) te za obavljanje raznih poslova, primjerice u lončarstvu.
Razmislite, gdje i kada vi upotrebljavate kotač?
Za kraj riješite sljedeći matematički diktat.
