

Što mislite, jesu li uspjeli točno izmjeriti duljinu staze oko jezera?
Hoćemo li uvijek moći mjeriti duljinu ruba kruga koracima?
Što ako je dio staze oko jezera neprohodan ili je neki krug neprikladan za hodanje oko njega i mjerenje?
Dobivamo li takvim mjerenjem točnu ili približnu duljinu ruba kruga?
Možemo li duljinu ruba kruga izmjeriti ravnalom?
Ne možemo uvijek na taj način mjeriti duljinu ruba kruga.
Na taj način dobivamo približnu duljinu.
Za točnu duljinu trebamo neku drugu metodu.
Krug je krivulja pa duljinu ruba kruga ne možemo izmjeriti ravnalom.
Duljinu ruba nekog pravokutnika, trokuta ili mnogokuta nazivamo opseg tog lika. Rub kruga je njegova pripadna kružnica.
Opseg kruga je duljina njegove pripadne kružnice.
Donesite od kuće neki kružni oblik, primjerice selotejp, kovanicu, poklopac ili nešto slično. Također vam treba komad konopca i ravnalo.
Ovaj projekt radite u parovima.
Konopac omotajte oko kružnog oblika samo jedanput, odrežite uže na tu duljinu, rastvorite ga i prislonite uz ravnalo.
Izradite tablicu i zapišite duljinu opsega svojega kružnog oblika u tablicu.
Zatim izmjerite promjer svojega kružnog oblika i također zapišite u tablicu.
Podijelite izmjerenu duljinu opsega kruga i promjer kruga.
Usporedite dobivene količnike s ostalim parovima u razredu.
Što primjećujete?
Zbog nepreciznog mjerenja dobili ste samo približno isti količnik, ali preciznim instrumentima dobili biste za krugove različitih promjera količnik duljine opsega kruga i promjera toga kruga uvijek isti broj.
Uvjerite se u to interaktivnom GeoGebrinom simulacijom. Odaberite kuglu ili loptu po želji, uočite duljinu promjera, kliknite na ljubičasti gumb i pogledajte duljinu najveće rubne kružnice tog tijela, odnosno njen opseg. Uočite omjer opsega i promjera te kružnice. Koji je to broj?
Mjerenjem i dijeljenjem opsega kruga i njegova promjera, i u interakciji smo dobili broj približne vrijednosti
Taj broj označavamo grčkim slovom i čitamo "pi".

Broj je beskonačni decimalni broj kojem se znamenke ne ponavljaju. Matematičari obilježavaju 14. ožujka kao Dan broja Oznaku je uveo u 18. stoljeću engleski matematičar William Jones, ali su za činjenicu da omjer opsega i promjera kruga nije racionalan broj znali još Babilonci. Nizozemski matematičar Ludolph van Ceulen je oko 1600. godine bez pomoći računala izračunao prvih decimala broja pa se po njemu katkad taj broj naziva i Ludolfov broj. Japanski matematičar Yasumasa Kanada je 2005. godine na superračunalu odredio decimala broja a izračun je trajao sati. Ljudi često pokušavaju izgovarati napamet što više znamenki broja a rekorder je -godišnji Japanac koji je zapamtio znamenki. Na slici je prvih decimala broja

Proslavite 14. ožujka Dan broja tako da pronađete na internetu još decimala broja Pokušajte ih zapamtiti što više. Organizirajte natjecanje u razredu tko je zapamtio najviše decimala. Ako želite, taj dan donesite u razred i pitu (pie) kružnog oblika.
Podaci na slici dobiveni su mjerenjem. Kad bismo vodoravno presjekli jelu Kraljicu šume iz park-šume Golubinjak u Gorskom kotaru, dobili bismo savršen krug. Jelu nećemo rezati. Odgovor ćemo saznati računanjem.
Pomoć:
Podijelite opseg jele s njezinim promjerom.
Ako dobijete broj vodoravni presjek jele je savršen krug.
Ako ne dobijete broj
vodoravni presjek jele nije savršen krug.
Postupak:
Izračunajte
Označimo opseg kruga s
a promjer s
Iz činjenice da je
slijedi formula za opseg kruga,
Za duljinu promjera kruga znamo da je jednaka dvostrukoj duljini njegova polumjera, tj.
pa formulu pišemo:
Formula za opseg kruga je
Primjer 1.
Izračunajmo opseg kruga polumjera
Opseg kruga možemo izračunati približno tako da uvrstimo u formulu za opseg kruga zadanu vrijednost polumjera i približnu vrijednost broja
najčešće na dvije decimale,
Ako želimo točnu vrijednost opsega, pišemo:

Pomoć:
Duljina lopatice je polumjer kruga koji opiše u jednom okretu.
Postupak:

Vjetroelektrana Vrataruša kod Senja nalazi se na obroncima Velebita. Izgrađena je 2009. godine. To je prva i najveća vjetroelektrana u Republici Hrvatskoj. Sastoji se od vjetroagregata pojedinačne snage (megavata). Visina vjetroagregata je metara.
Točna vrijednost opsega kruga polumjera je
Pomoć:
Izračunajte približnu vrijednost opsega poklopca oblika kruga kreme za njegu usana, promjera
Pomoć:
Polumjer kruga je
Postupak:
Primjer 2.
Promjer kotača brdskog bicikla je inča.
- Ako znamo da je koliki je opseg kotača?
- Koliki put prijeđe bicikl kad kotači naprave puni okret?
- Koliko se puta kotači okrenu kad bicikl prijeđe
Pomoć:
Prijeđeni put podijelite s opsegom kotača.
Postupak:
Opseg manjeg kotača
Opseg većeg kotača
Primjer 3.
Izračunajmo polumjer kruga kojem je opseg
Uvrstimo zadani opseg u formulu
Polumjer kruga je
Izračunajte polumjer kruga opsega
Uvrstimo zadani opseg u formulu i dobijemo jednadžbu
Polumjer kruga je
Žica je duga Ako je savijemo u krug, koliki će biti polumjer toga kruga?
Pomoć:
Duljina žice je opseg kruga.
Postupak:

Pomoć:
Postupak:
Opseg jednog namotaja je
Promjer koluta
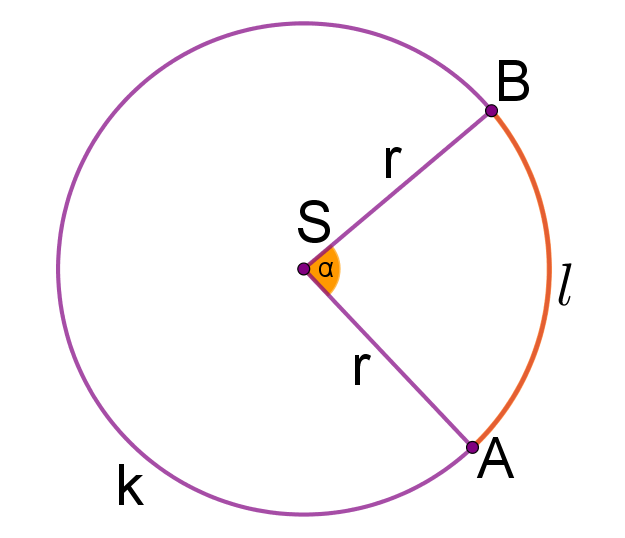
Kružni luk je dio kružnice, a duljina kružnice je opseg kruga. Ako možemo računati duljinu kružnice, možemo računati i duljinu njezinih dijelova.
Oznaka duljine kružnog luka je malo pisano slovo kao na slici.
Na slikama su kružnice istog polumjera. Sa slika vidimo da ako je veći središnji kut, onda je pripadni kružni luk.
Pomoć:
Pažljivo pogledajte slike.
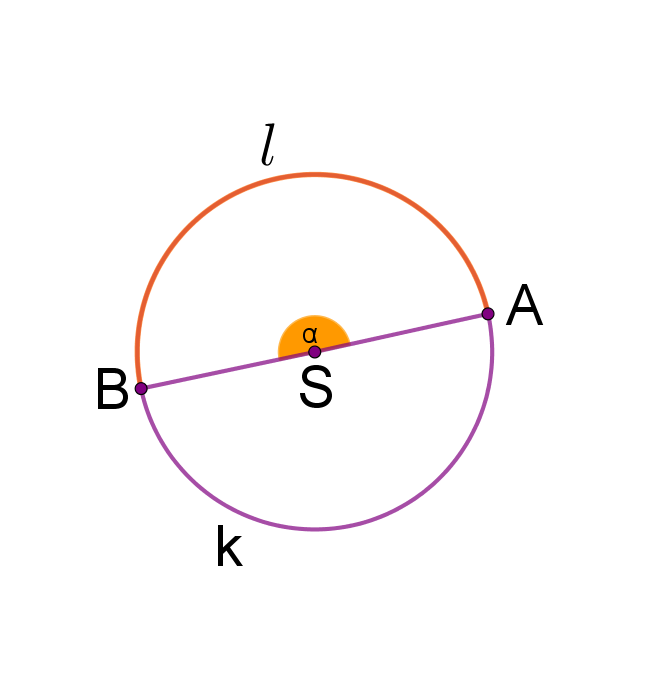
Duljina polukružnice je opsega kruga, tj. u ovom slučaju
Pomoć:
Polukružnica je pola kružnice.
Središnji kut od
je pola punog kuta od
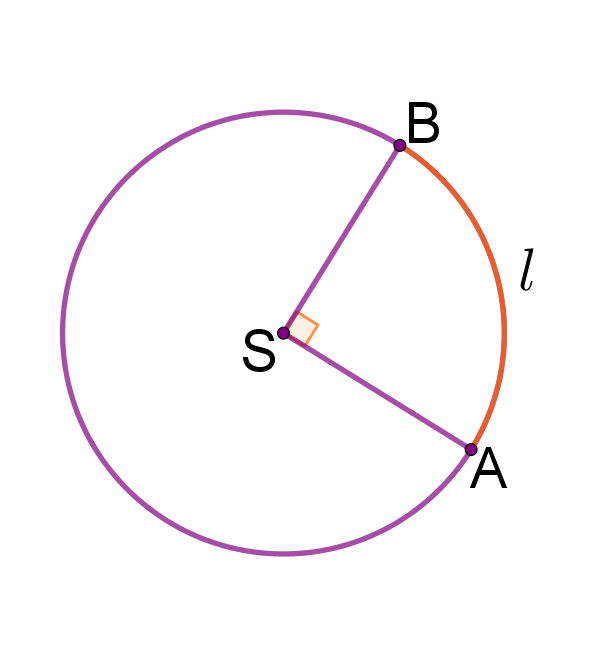
Središnji kut na slici je kut i iznosi .
Pomoć:
Pažljivo pogledajte sliku.
Središnji kut od je punog kuta od .
Pomoć:
Prisjetite se veličina kutova i njihovih naziva.
Duljina pripadnog kružnog luka je opsega kruga.
Pomoć:
Ako središnji kut podijelimo na jednaka dijela, i krug je podijeljen na jednaka dijela, pa je i kružnica podijeljena na jednaka dijela.
Cijeloj kružnici pripada središnji kut od Spojite parove dijelova kružnice i pripadnog središnjeg kuta.
|
šestina kružnice
|
središnji kut |
|
desetina kružnice
|
središnji kut |
|
petina kružnice
|
središnji kut |
|
trećina kružnice
|
središnji kut |
Pomoć:
Nacrtajte kružnicu bilo kojeg polumjera. Puni kut iznosi Podijelite puni kut, nacrtajte kutomjerom središnji kut.
Polumjer kruga je Izračunajte opseg toga kruga.
Opseg kruga je duljina pripadne kružnice. Za krug polumjera spojite parove dijela kružnice i duljine pripadnog kružnog luka.
|
šestina kružnice
|
|
|
četvrtina kružnice
|
|
|
trećina kružnice
|
|
|
dvanaestina kružnice
|
Pomoć:
Podijelite kružnicu na tri, četiri, šest i dvanaest dijelova, zatim podijelite opseg s tri, četiri, šest ili dvanaest.
Pogledajte još jedanput prethodna četiri zadatka i razmislite o promjenama veličine središnjeg kuta i duljine pripadnog kružnog luka. Što možete zaključiti?
Koliko se puta povećala veličina središnjeg kuta, toliko se puta duljina pripadnog kružnog luka iste kružnice. Koliko se puta smanjila veličina središnjeg kuta, toliko se puta duljina pripadnog kružnog luka iste kružnice.
Pomoć:
Dobro pogledajte prethodne zadatke i promotrite veličine središnjih kutova i duljine pripadnih kružnih lukova.
Duljina kružnog luka i veličina pripadnog središnjeg kuta iste kružnice međusobno su veličine.
Pomoć:
Ako za dvije veličine vrijedi: koliko puta se poveća ili smanji jedna veličina, toliko će se puta povećati ili smanjiti i druga veličina, za te dvije veličine kažemo da su proporcionalne veličine.
Duljina kružnog luka
i veličina pripadnog središnjeg kuta
su proporcionalne veličine pa vrijedi razmjer:
duljina kružnog luka
: opseg kruga
= veličina pripadnog središnjeg kuta
: veličina punog kuta
, odnosno
Riješimo razmjer
skratimo razlomak s i dobijemo formulu za duljinu kružnog luka
Duljina kružnog luka kružnice polumjera s pripadnim središnjim kutom računa se prema formuli:
Primjer 4.
Polumjer kruga je Izračunajmo duljinu kružnog luka kojem pripada središnji kut od
Duljinu kružnog luka računamo prema formuli
ili približno (za približno računanje preporučujemo upotrebu džepnog računala)
Polumjer kruga je
Izračunajte duljinu kružnog luka kojem pripada središnji kut od
Uvrstimo i u formulu za duljinu kružnog luka.
Primijetimo da su u primjeru i zadatku središnji kutovi jednakih veličina, ali su polumjeri kružnica različitih duljina. Što možete zaključiti za duljine pripadnih kružnih lukova?
Ako je polumjer kružnice dvostruko dulji, za središnji kut jednake veličine dobit ćemo kružni luk.
Pomoć:
Usporedite polumjere, središnje kutove i duljine kružnih lukova primjera i zadatka.
Duljina kružnog luka i duljina polumjera kružnice međusobno su veličine.
Pomoć:
Ako za dvije veličine vrijedi: koliko se puta poveća jedna veličina, toliko će se puta povećati i druga veličina, za te veličine kažemo da su proporcionalne.
Izračunajte duljinu kružnog luka kojem pripada središnji kut kružnice polumjera
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Uvrstite duljinu polumjera i veličinu kuta u formulu za duljinu kružnog luka, skratite razlomak i pomnožite preostale brojeve ili zadatak riješite logički s pomoću dijelova punog kuta i proporcionalno dijela opsega kruga.
Velika kazaljka sata duga je Koliki kut napravi kad se pomakne od broja do broja
Pomoć:
Sat je podijeljen na brojeva. Između svaka dva broja je kut
Postupak:
Pomoć:
Primjer 5.
Izračunajmo duljinu polumjera kruga ako je duljina kružnog luka s pripadnim središnjim kutem
U formulu za duljinu kružnog luka uvrstimo poznate podatke
skratimo razlomak s
Duljina polumjera kruga je
Izračunajte duljinu promjera kruga ako je duljina kružnog luka približno
i pripadni središnji kut
U formulu za duljinu kružnog luka uvrstite poznate podatke i približnu vrijednost broja
(za račun preporučujemo upotrebu džepnog računala)
Promjer kruga je
Primjer 6.
Duljina promjera kruga je Izračunajmo veličinu središnjeg kuta kružnog luka duljine približno
Polumjer kruga je Nakon uvrštavanja podataka u formulu za duljinu kružnog luka, dobijemo jednadžbu iz koje slijedi
Veličina središnjeg kuta je
Duljina zavoja ceste je Izračunajte pripadni središnji kut zavoja ako je njegov polumjer
Pomoć:
Duljina zavoja je duljina kružnog luka.
Postupak:
Primjer 7.
Izračunajmo duljinu kružnog luka nad jednom stranicom pravilnog deveterokuta upisanog u kružnicu opsega
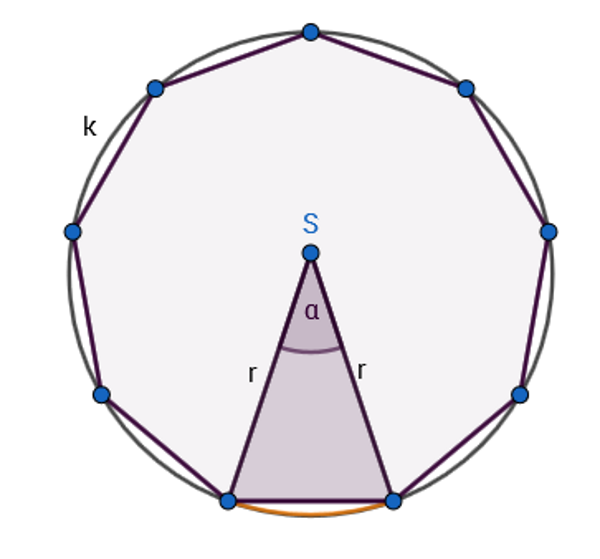
Iz opsega kruga izračunamo polumjer
Središnji kut karakterističnog trokuta pravilnog deveterokuta je
To je ujedno središnji kut kružnog luka nad jednom stranicom pravilnog deveterokuta. Uvrstimo te podatke u formulu za duljinu kružnog luka.
Duljina kružnog luka nad jednom stranicom pravilnog deveterokuta je
Odredite opseg kruga opisanog pravilnom šesterokutu kojem je duljina kružnog luka nad jednom stranicom
Središnji kut pravilnog šesterokuta je Iz jednadžbe dobijemo a opseg kruga opisanog tom pravilnom šesterokutu je
Rješenje možete dobiti i iz omjera opsega kružnice i duljine kružnog luka.
U kružnicu promjera
upisan je pravilni mnogokut. Koji je to mnogokut ako je duljina kružnog luka nad jednom stranicom približno
U formulu za duljinu kružnog luka uvrstimo podatke i dobijemo Iz formule za veličinu središnjeg kuta pravilnog mnogokuta dobijemo
Mnogokut je pravilni deseterokut.
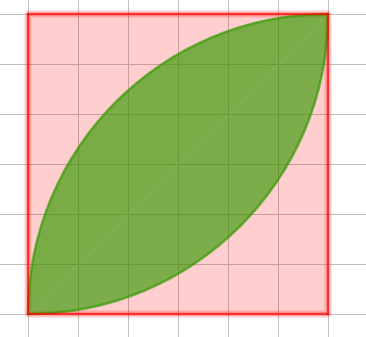
Izračunajte duljinu zelenog konca potrebnog za obrub zelenog lika koji predstavlja motiv listića na platnenoj božićnoj salveti. Duljina stranice kvadrata je 3 cm, a konca treba tri puta više od duljine obruba listića.
Rub listića sastoji se od dva kružna luka polumjera
i pripadnog središnjeg kuta od
Duljina jednog kružnog luka je
duljina ruba listića je
a duljina konca je
.
Zelenog konca treba

Promjer prednjeg kotača traktora je a stražnjeg Koliki je put prešao traktor ako je stražnji kotač načinio okreta manje nego prednji.
Označimo s broj okreta prednjeg kotača i s opseg prednjeg kotača, a s broj okreta stražnjeg kotača i opseg stražnjeg kotača. Tada je Put koji je prešao prednji kotač jednak je putu koji je prešao stražnji kotač. Put koji je prešao prednji kotač je a put koji je prešao stražnji kotač je . Izjednačimo te jednadžbe i uvrstimo .
Put je
Traktor je prešao put od
U ovoj jedinici naučili ste povezati duljinu promjera i opseg kruga te veličinu središnjeg kuta i duljinu kružnog luka iste kružnice. Upoznali ste beskonačni decimalni broj i vidjeli primjenu znanja opsega kruga i duljine kružnog luka u problemima iz matematike i svakodnevnog života.
Na kraju provjerite koliko ste naučili kratkom procjenom znanja.
Kako nazivamo broj koji dobijemo kao količnik opsega i promjera kruga?
Pomoć:
Pogledajte dio jedinice o tom broju i prisjetite se naziva beskonačnog decimalnog broja, koji ima i svoj dan, 14. ožujka.
Formula za opseg kruga je
Pomoć:
Formula za opseg kruga je
Pomoć:
Zapišite barem dvije decimale broja
ali možete zapisati i više decimala ako ste ih zapamtili ili pronašli na internetu.
Izračunajte točno ili približno opseg kruga ako je zadana duljina promjera
ili polumjera
kruga.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Pomoć:
Pogledajte formulu za duljinu kružnog luka.
Izračunajte točno ili približno duljinu kružnog luka ako su zadani polumjer
kruga i središnji kut
koji pripada tom kružnom luku.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Postupak:
Razlomke skratite nakon uvrštavanja podataka u formulu
.
Opseg kruga je a duljina kružnog luka Izračunajte veličinu pripadnog središnjeg kuta.
Pomoć:
Iz opsega kruga izračunajte polumjer kruga.
Prema formuli za duljinu kružnog luka i polumjera odredite veličinu središnjeg kuta.
Postupak:
Pomoć:
Broj zaokružite na najmanje dvije decimale.
Pomoć:
Broj zaokružite na najmanje dvije decimale.
Na rub stolnjaka kružnog oblika našiveno je približno ukrasne vrpce. Izračunajte promjer stolnjaka.
Pomoć:
Promjer u metrima zaokružite na jednu decimalu. Promjer u centimetrima zaokružite na desetice. Duljina vrpce je također zaokružena na jednu decimalu.