

Sve je moguće uz malo matematike, zar ne?
Za uvježbavanje sličnosti trokuta predlažemo vam nekoliko zadataka koje možete samostalno riješiti u bilježnicu ili u nekom interaktivnom elementu. Posljednjh nekoliko zadataka namijenjeno je onima koji žele znati više, ali svi ih možete pokušati riješiti. Nakon što riješite zadatke, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili ih zamolite da vam pomognu ako vam je neki zadatak težak.

Dužinu proizvoljne duljine podijelite na jednakih dijelova koristeći se Talesovim poučkom o proporcionalnim dužinama.

Dužinu
proizvoljne duljine podijelite točkom
u omjeru
koristeći se Talesovim poučkom o proporcionalnim dužinama.
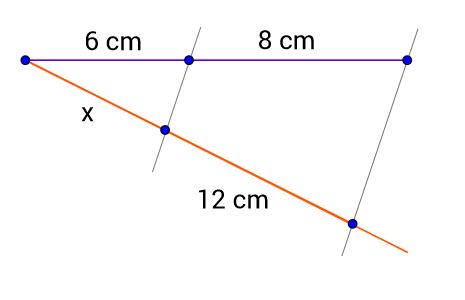
Izračunajte nepoznatu duljinu dužine na slici (sve su mjere izražene istom mjernom jedinicom) koristeći se Talesovim poučkom o proporcionalnim dužinama.
Prema Talesovu poučku usporedni pravci odsijecaju proporcionalne dužine, zato vrijedi
Trokuti su slični ako su im omjeri duljina odgovarajućih stranica jednaki i kutovi jednakih veličina. Dovucite nazive poučaka na odgovarajuće elemente koji su prema određenom poučku dovoljni da se pokaže sličnost trokuta.
|
SSS poučak o sličnosti trokuta
|
Omjeri svih triju stranica |
|
KK poučak o sličnosti trokuta
|
Omjeri dviju stranica i kut između |
|
SKS poučak o sličnosti trokuta
|
Dva sukladna kuta |
Pomoć:
Pozorno pročitajte nazive svakog poučka, u kojima
označava kut, a
označava stranicu.
Svjetionici omogućuju sigurnu dnevnu i noćnu plovidbu morem. Oni su kao semafori na moru. Izgrađeni su na najistaknutijim i na najudaljenijim točkama na moru. Najviši je svjetionik na Jadranu svjetionik Rt Veli rat u Zadarskom arhipelagu. Kula svjetionika visoka je Više o svjetionicima možete saznati ovdje.
Koliko je svjetionik udaljen od obale?
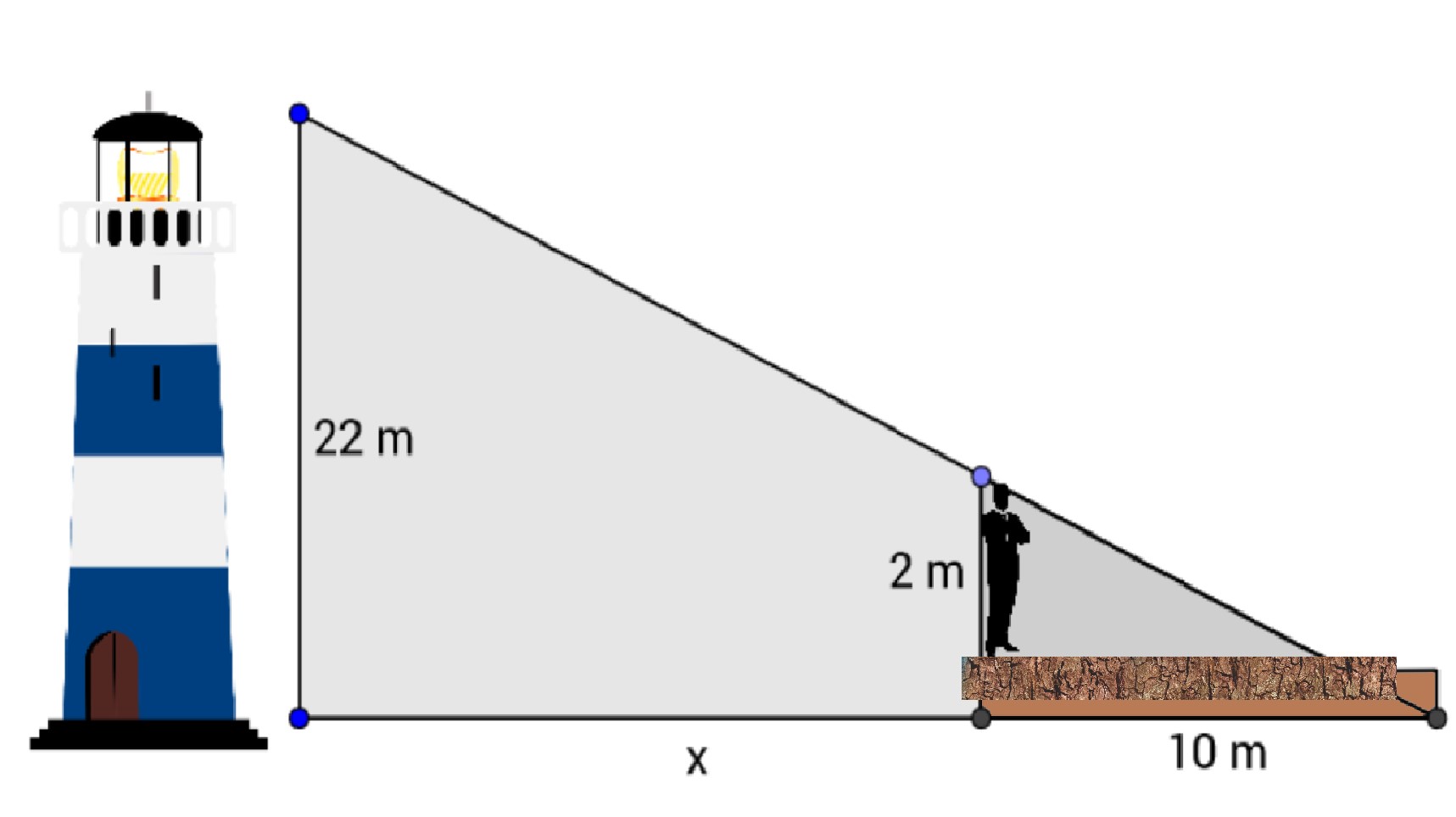
Pomoć:
Uočite kako se na slici nalaze dva slična trokuta. Stavite odgovarajuće stranice u omjer i pronađite rješenje. Rješenje zapišite u obliku cijelog broja na za to predviđeno mjesto. Obrati pozornost na duljinu mola.
Trokut
sličan je manjem trokutu
s koeficijentom
Izračunajte nepoznate duljine stranica tih trokuta ako je zadano
i
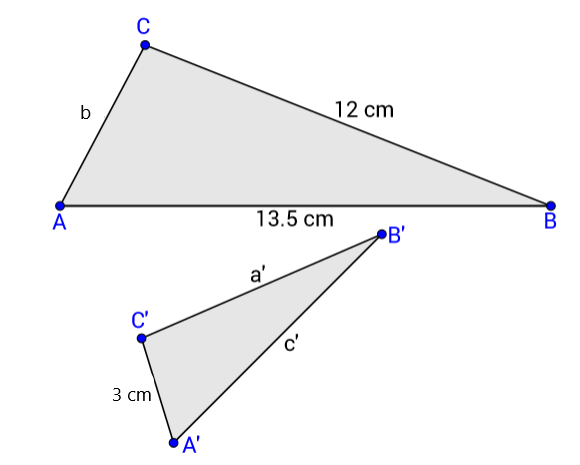
Nacrtajmo skicu.
Trokuti su slični s koeficijentom veći trokut
manji trokut
Duljine nepoznatih stranica su i
U Minimundusu se nalazi više od
minijaturnih modela građevina izrađenih u mjerilu
Kolika je visina minijaturne građevine Eiffelova tornja u Minimundusu ako je stvarna visina tornja
Pomoć:
Rješenje dobijete tako da visinu stvarnog Eiffelova tornja podijelite s
Odgovor upišite u obliku cijelog broja na za to predviđeno mjesto.

Minimundus je park minijaturnih građevina u Klagenfurtu u Austriji. Nalazi se na jezeru Wörthsee i sadržava modela poznatih građevina iz zemalja koje su izađene u mjerilu
Više o Minimundusu možete pročitati na službenoj stranici parka.
Odaberite jednu manju građevinu u svojemu mjestu i saznajte njezinu visinu. Izradite minijaturni model te građevine prema uzoru na one u Minimundusu. Možete ih izraditi i nekoliko te organizirati izložbu.
Omjer odgovarajućih stranica sličnih trokuta je Ako znate da je opseg većeg trokuta koliki je opseg manjeg trokuta?
Označite opseg manjeg trokuta s
Duljine stranica jednog trokuta iznose i Opseg njemu sličnog trokuta iznosi Izračunajte duljine stranica drugog trokuta.
Označimo vrhove ovog trokuta s a opseg s
Iz slijedi
Iz slijedi
Iz slijedi
Duljine stranica trokuta iznose i
Nacrtajte trokut
s duljinama stranica
i
Zatim nacrtajte njemu sličan trokut tako da novi trokut i početni trokut budu u omjeru
Zadatak riješite tako da prvo izračunate duljine odgovarajućih stranica i nacrtate oba trokuta u bilježnici. Zatim sve provjerite u GeoGebrinu interaktivnom predlošku.
Ako je omjer znači da je novi trokut sličan početnom s koeficijentom Stranice novog trokuta bit će puta dulje od duljina stranica početnog trokuta.
Zadatak ste mogli riješiti i s pomoću razmjera.
Duljine stranica novog trokuta iznose i
Zadatci sa sličnim trokutima katkad se pojavljuju na Državnoj maturi pa predlažemo da pogledate i sljedeće zadatke.
Omjer površina sličnih trokuta iznosi
Ako je opseg većeg trokuta
koliki je opseg manjeg trokuta?
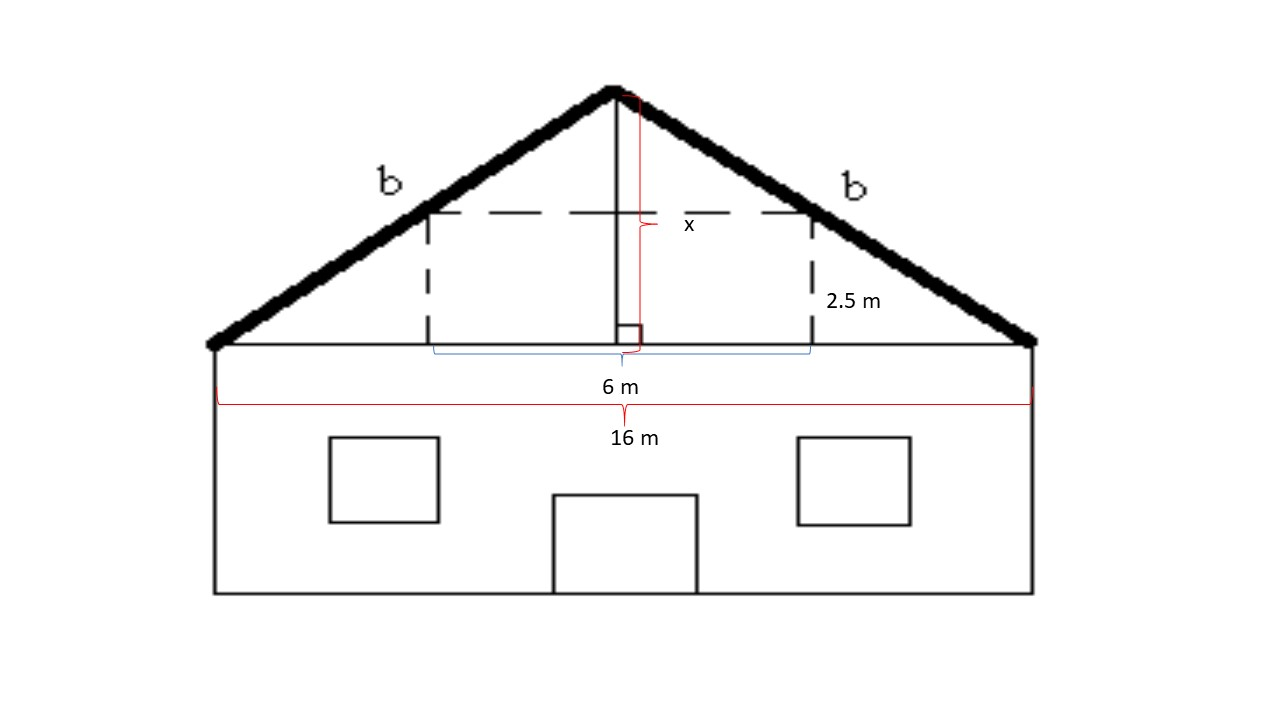
Marija će u potkrovlju kuće dobiti svoju sobu. Visina sobe bit će
a širina
Ako je širina kuće
kolika mora biti visina krova?
Na zapuštenom zemljištu pokraj grada želi se izgraditi trgovački centar. Bilo bi preskupo i besmisleno odmah prionuti na posao, prvo treba napraviti plan i projekt u umanjenom mjerilu. Danas se to sve radi računalno, čak se može i isprintati 3D-tehnologijom, da si investitori mogu bolje predočiti kako će sve to izgledati. Nekad se sve radilo ručno, nacrti, makete od kartona... Svaka duljina mora biti umanjena s istim koeficijentom sličnosti. Od davnina su ljudi radili geografske karte, no da bi bile dobre, moraju biti nacrtane precizno i u točnom omjeru. Danas na bilo kojem mediju možete učitati kartu i proporcionalno ju povećavati i smanjivati.
Ako želite napraviti veliku reklamu za svoj proizvod, prvo ćete na računalu nacrtati malu sliku, a onda ju povećati na veliku dimenziju. Za proučavanje malih objekata, primjerice zuba, atoma, DNK i slično, izrađuju se proporcionalno uvećani modeli. U učionici biologije zasigurno imate takve modele.
Sjetite se još nekih primjera u kojima svakodnevno upotrebljavamo sličnost, a toga uopće nismo svjesni. Čini nam se da je to jednostavno tako.
Na kraju pročitajte zanimljivost o trokutu Sierpinskog i pokušajte nacrtati što više trokutića kao što je objašnjeno u zanimljivostima, a vidi se u interaktivnoj GeoGebri autorice Julijane Novaković.
Trokut Sierpinskog nastaje tako da nacrtamo prvo veliki jednakostranični trokut, označimo polovišta njegovih stranica, spojimo polovišta u novi trokut, zatim izvan tog trokuta dobijemo tri nova trokuta kojima opet označimo polovišta stranica i spojimo ih u nove trokute, i tako što više puta uspijemo. Postupak takvog ponavljanja naziva se iteracija. Likovi dobiveni iteracijom su fraktali. Karakterizira ih to da se isti lik stalno ponavlja tako da je svaki manji dio sličan svojemu prethodnom dijelu. Fraktale susrećemo i u prirodi, primjerice paprat, brokula ili šenon. Zanimljivo je da se med kristalizira u fraktalne oblike. Više o fraktalima i o tome kako nastaju možete pročitati u seminarskom radu Mladena Paušića, s Fakulteta elektrotehnike i računarstva.
Iteracijom dobivamo trokute slične početnom trokutu. Mogu se tako crtati i drugi likovi, čak i tijela.
Posebno je zanimljivo to da što više iteracija crtamo, opseg lika postaje sve veći, a površina tamnog dijela sve manja. Posebno lijepo izgleda kada se to napravi od nekog čvrstog materijala i kada se bijeli trokuti izrežu. Na slici dolje je tijelo koje se sastoji od
pravilnih peterokuta, dodekaedar. Od njega je iteracijom napravljen dodekaedar Sierpinskog.
Nacrtajte trokute Sierpinskog u raznim bojama i napravite izložbu u učionici.