Matematika 7 - Aktivnosti za samostalno učenje

Riješite, provjerite i podijelite

Za uvježbavanje prikupljanja i analize podataka predlažemo vam nekoliko zadataka koje možete samostalno riješiti u bilježnici ili u nekom interaktivnom elementu. Nekoliko posljednjih zadataka je za one koji žele znati više, ali svi ih možete pokušati riješiti. Nakon što riješite zadatke, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili ih zamolite da vam pomognu ako vam je neki zadatak težak.

Kolekcija zadataka 1

Zadatak 1.

U tablici su prikazani podatci o djelatnosti hitne medicinske pomoći iz 2010. godine. Izvor podataka je DZS.

Intervencije	Broj intervencija
Intervencija u ordinaciji	$1 026 000$
Intervencije u kući bolesnika	$187 000$
Intervencije na terenu	$69 000$
Sanitetski prijevoz	$542 000$

Podaci u prikazuju vrstu i broj intervencija hitne medicinske pomoći u 2010. godini.

Vrsta intervencije je , a broj intervencija je skupa podataka.

Pomoć:

Pročitajte pažljivo jedinicu Prikupljanje podataka.

null

Zadatak 2.

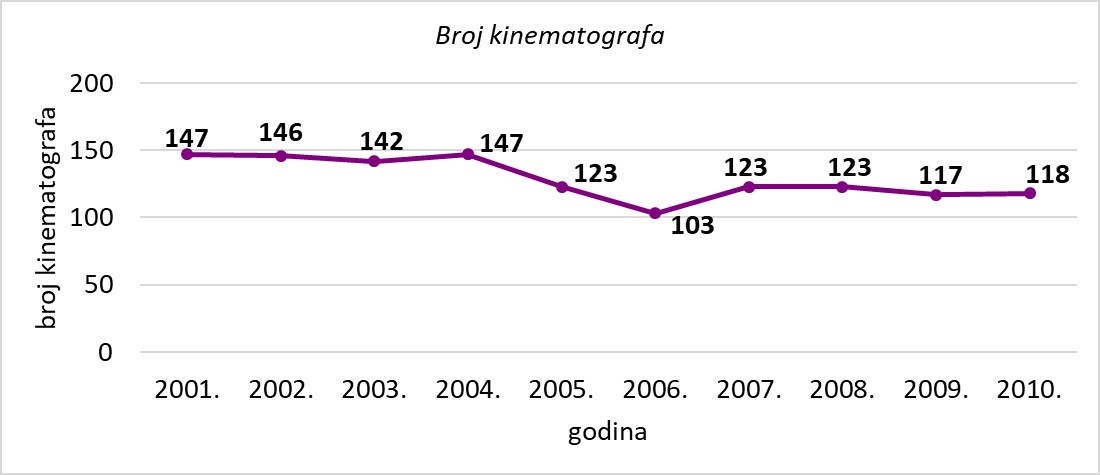
Na slici je linijski dijagram o broju kinematigafa od 2001. do 2010. godine

U linijskom je dijagramu prikazan broj kinematografa u Republici Hrvatskoj od 2001. do 2010. godine. (Izvor: DZS)

Dopunite rečenice.

Od godine 2004. do 2006. broj kinematografa u Republici Hrvatskoj naglo:

raste
Pozorno pogledajte dijagram.

pada.

Pomoć:

Kod linijskog dijagrama pratimo linije slijeva nadesno.

null
Od godine 2006. do 2007. broj kinematografa u Republici Hrvatskoj :

raste

pada.
Pozorno pogledajte dijagram.

Pomoć:

Kod linijskog dijagrama pratimo linije slijeva nadesno.

null

Zatvori

Kolekcija zadataka 2

Zadatak 3.

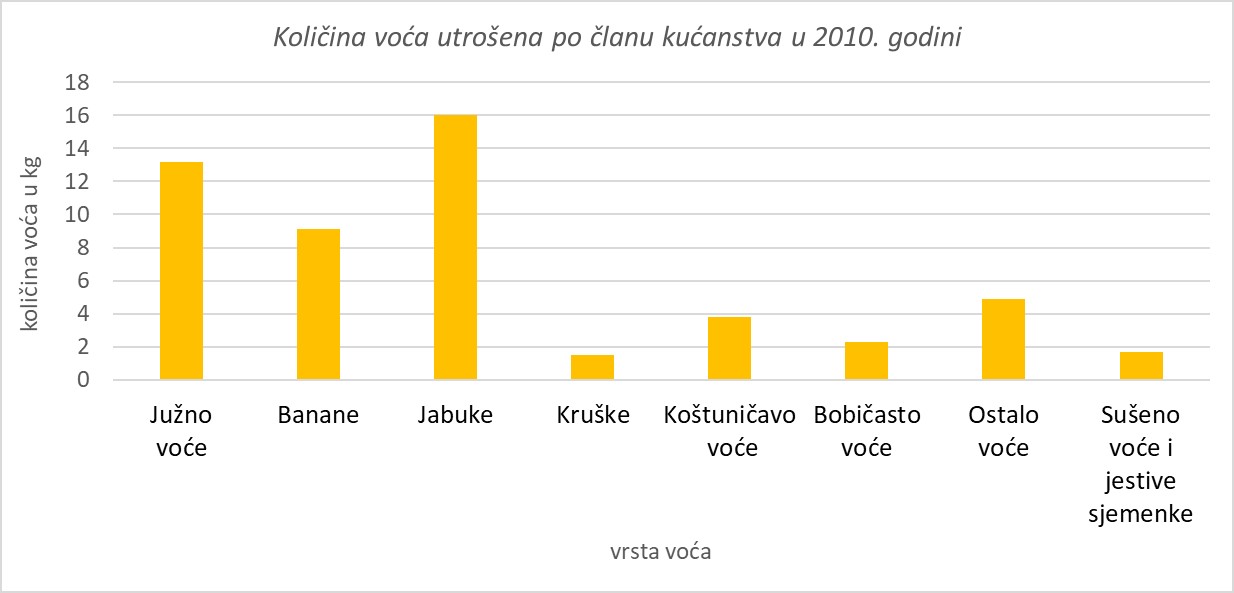
U tablici su podatci o prosječnoj godišnjoj količini voća u kilogramima utrošenoj po članu kućanstva u Republici Hrvatskoj u 2010. godini.

Vrsta voća	Količina voća po članu kućanstva u kg
južno voće	$13.2$
banane	$9.1$
jabuke	$16.0$
kruške	$1.5$
koštuničavo voće	$3.8$
bobičasto voće	$2.3$
ostalo voće	$4.9$
sušeno voće i jestive sjemenke	$1.7$

Izvor: DZS

Nacrtajte stupčasti dijagram frekvencija za te podatke.
Kojeg je voća najviše utrošeno po članu kućanstva 2010. godine?
Kojeg su voća članovi kućanstva najmanje pojeli u 2010. godini?
Koliko je kilograma voća prosječno pojeo jedan član kućanstva u 2010. godini?
Koliko bi to približno kilograma bilo na tjedan po članu kućanstva?
Koliko posto se pojelo bobičastog voća po članu kućanstva u 2010. godini u odnosu prema ukupnom voću koje je utrošeno po članu kućanstva te godine?

na slici je stupčasti dijagram koji pokazuje količinu voća utrošenog po članu kućanstva u 2010. godini

Stupčasti dijagram frekvencija
Najviše se pojelo jabuka.
Najmanje se jelo krušaka.
Svaki je član kućanstva 2010. godine pojeo prosječno $52.5 kg$ voća.
To bi na tjedan bilo približno $1 kg$ voća po članu kućanstva.
Bobičastog voća u odnosu prema ukupnom voću pojelo se $4.38 % .$

Zadatak 4.

Andrea je otvorila trgovinu prirodnih proizvoda za njegu tijela. Prvi je mjesec zaradila $2 000 kn,$ drugi $3 000 kn,$ treći $12 000 kn,$ četvrti $18 000 kn,$ peti $6 000 kn$ i šesti mjesec $4 000 kn .$

Odredite frekvenciju i relativnu frekvenciju Andreine zarade u prvih šest mjeseci od otvaranja trgovine.
Koji je mjesec ostvarila najveću, a koji najmanju zaradu? Koliki je udjel zarade tih mjeseci u ukupnoj zaradi?
Nacrtajte stupčasti dijagram relativnih frekvencija.
Izračunajte Andreinu prosječnu mjesečnu zaradu.

a. Frekvenciju i relativna frekvencija Andreine zarade u prvih šest mjeseci

Mjesec	Frekvencija	Relativna frekvencija	Relativna frekvencija u obliku postotka
1.	$2 000$	$0.01$	$1 %$
2.	$3 000$	$0.15$	$15 %$
3.	$2 500$	$0.13$	$13 %$
4.	$3 500$	$0.18$	$18 %$
5.	$6 000$	$0.3$	$30 %$
6.	$3 000$	$0.15$	$15 %$
Ukupno	$20 000$	$1$	$100 %$

b. Najveću je zaradu imala peti mjesec kad je ostvarila $30 %$ ukupne zarade. Najmanju je zaradu imala prvi mjesec kad je ostvarila $1 %$ ukupne zarade.

Na slici je stupčasti dijagram relativnih frekvencija koji prikazuje zaradu u prvih šest mjeseci od otvaranja trgovine. — c) Stupčasti dijagram relativnih frekvencija

c. Stupčasti dijagram relativnih frekvencija.

d. Prosječnu zaradu izračunajte s pomoću formule za aritmetičku sredinu podataka.

$\begin{array}{l} \bar{x_{n}} = \frac{2 000 + 3 000 + 2 500 + 3 500 + 6 000 + 3 000}{6} \end{array}$

$\bar{x_{n}} = 3 333.33 kn$

Prosječna zarada bila joj je $3 333.33 kn .$

Zatvori

Projekt

Zamislite da vodite poduzeće s prijateljem iz razreda. Osmislite čime će se ono baviti i kako će se zvati. Odredite koliki su vam troškovi svaki mjesec, ali i kolika vam je zarada. Koliki udjel određenog proizvoda ste prodali. Podatke prikažite s pomoću tablica i dijagrama. Prikažite svoj rad plakatom.

Zadatak 5.

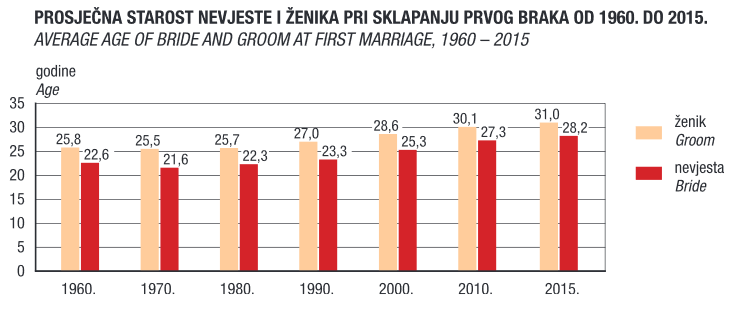
Pogledajte dijagram i odgovorite na pitanja. (Izvor: DZS, Statistički ljetopis 2016.)

Koje je godine prosječna dob ženika bila najveća?
Koje je godine prosječna dob nevjeste bila $22.3$ godine?
Usporedite i objasnite prosječnu dob pri ulasku u brak $1970 .$ godine i $2015 .$ godine.

Na slici je višestruki stupčasti dijagram koji pokazuje prosječnu dob stupanja u brak

Prosječna dob ženika bila je najveća
Pozorno pogledajte dijagram.
. godine.

Pomoć:

Odgovor upišite u obliku cijelog broja na za to predviđeno mjesto.

null
Prosječna dob nevjeste $22.3$ godine bila je
Pozorno pogledajte dijagram.
. godine.

Pomoć:

Odgovor upišite u obliku cijelog broja na za to predviđeno mjesto.
Prosječna dob pri ulasku u brak $2015 .$ godine bila je nego prosječna dob $1970 .$ godine.

Pomoć:

Pozorno pogledajte dijagram.

Projekt

Zamijetite da je većina podataka preuzeta od Državnog zavoda za statistiku. U Statističkom ljetopisu 2016. godine pronađite dio s tablicama za obrazovanje. Podijelite se u skupine. Izaberite jednu tablicu, pripremite pitanja vezana za nju. Izaberite dijagram i pripremite pitanja za njegovu analizu. Dajte svoja pitanja drugoj skupini, a ona neka vama da svoja. Napravite izvješće o aktivnosti koristeći se jednim od online alata za infografiku. Neki od njih spomenuti su i u ovoj cjelini.

Zadatak 6.

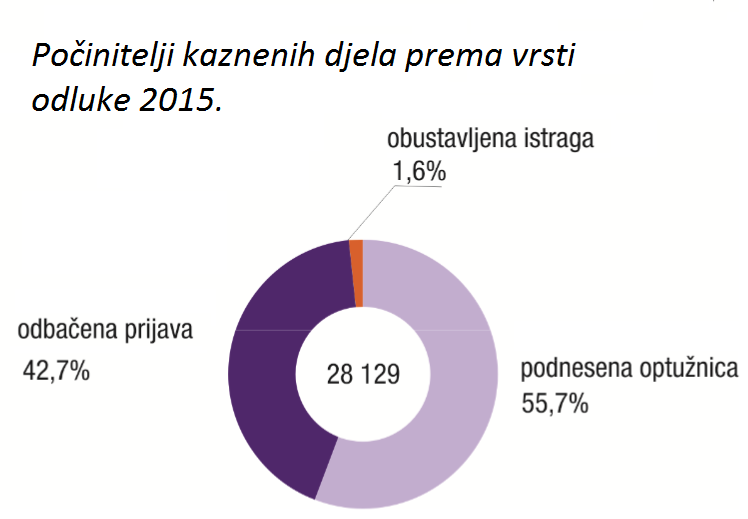
U Hrvatskoj je bilo $28 129$ potencijalnih počinitelja kaznenih djela čija je podjela prema vrsti odluke suda prikazana kružnim dijagramom.

Koliko ima počinitelja kojima je prekinuta istraga?
Koliko ima počinitelja kojima je odbačena prijava?

Imajte na umu da mnogi od potencijalnih počinitelja kaznenih djela nisu to isto djelo i počinili te je zato protiv njih prekinuta istraga ili odbačena prijava.

Na slici je broj potencijalnih počinitelja kaznenih djela čija je podjela prema vrsti odluke suda prikazana kružnim dijagramom.

Protiv
Rješenje zaokružite na cijeli broj.
počinitelja kaznenih djela odbačena je prijava.

Pomoć:

Rješenje napišite u obliku cijelog broja na za to predviđeno mjesto.

null
Protiv
Rješenje zaokružite na cijeli broj.
počinitelja prekinuta je istraga.

Pomoć:

Rješenje napišite u obliku cijelog broja na za to predviđeno mjesto.

null

Kutak za znatiželjne

Kolekcija zadataka 3

Zadatak 7.

Najviša prosječna visina snijega na vrhovima hrvatskih planina jedne zime bila je $108 cm .$ Podatci za vrh Vojak na Učki obrisali su se. Izračunajte s pomoću preostalih podataka iz tablice visinu snijega na vrhu Vojak te zime. Istražite gdje se nalaze ostali vrhovi.

Vrh	Visina snijega u cm
Zavižan	$207$
Sljeme	$25$
Štimčev vrh	$162$
Veliki Snježnik	$178$
Sveta Gera	$59$
Sveti Jure	$120$
Vojak

Prosječna visina snijega $\bar{x}$ je $108 cm .$ Jedan podatak nam je nepoznat, označimo ga s $x,$ ostali podatci su nam poznati. Prosječna visina računa se tako da sve podatke zbrojimo i podijelimo s brojem vrhova. Uvrstimo podatke u jednadžbu.

$\bar{x} = \frac{207 + 25 + 162 + 178 + 59 + 120 + x}{7}$

$108 = \frac{207 + 25 + 162 + 178 + 59 + 120 + x}{7}$

$108 = \frac{751 + x}{7}$ $/ \cdot 7$

$756 = 751 + x$

$x = 5 cm .$

Najviša visina snijega na Vojaku te zime bila je $5 cm .$

Zadatak 8.

Prosječna visina djece u razredu od $23$ učenika je $150 cm .$ Kad u razred dođe jedan novi učenik, prosječna visina učenika u razredu je $151 cm .$ Koliko je visok dječak koji je došao u taj razred?

Prosječna visina $23$ učenika $\bar{x}$ je $150 cm .$ Postavimo jednadžbu tako da izračunamo zbroj svih visina učenika.

$\bar{x} = \frac{x_{1} + x_{2} + . . . + x_{23}}{23}$

$150 = \frac{x_{1} + x_{2} + . . . + x_{23}}{23}$ $/ \cdot 23$

$x_{1} + x_{2} + . . . + x_{23} = 3 450 .$

Kad u razred dođe novi učenik, učenika je $24,$ a njihova prosječna visina sada je $151 cm .$ Postavimo novu jednadžbu.

$\bar{x} = \frac{x_{1} + x_{2} + . . . + x_{23} + x_{24}}{24}$

$151 = \frac{x_{1} + x_{2} + . . . + x_{23} + x_{24}}{24}$ $/ \cdot 24$

$3 624 = x_{1} + x_{2} + . . . + x_{23} + x_{24}$

Iz prve jadnadžbe dobili smo da je $x_{1} + x_{2} + . . . + x_{23} = 3 450 .$ Uvrstimo taj izraz u novu jednadžbu i riješimo.

$3 624 = 3 450 + x_{24}$

$x_{24} = 174 cm$

Novi je dječak visok $174 cm .$

Zadatak 9.

Proglašavanje mjera zaštite od poplave ovisi o visini vodostaja neke rijeke. Stupnjevi mjera zaštite od poplave su:

normalno stanje vodostaja
pripremno stanje
redovite mjere zaštite od poplave
izvanredne mjere zaštite od polave i
izvanredno stanje.

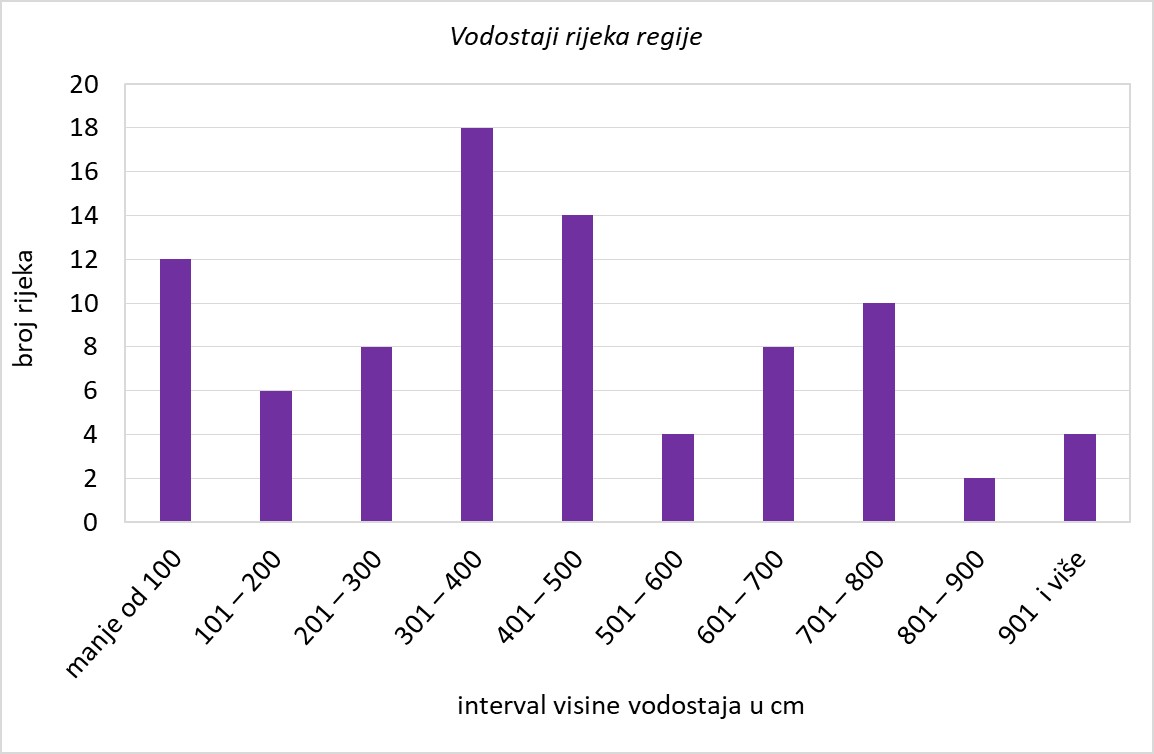
Na slici je stupčasti dijagram vodostaja rijeka neke regije

Na slici su prikazani vodostaji rijeka jedne regije u jednom satu. Pravokutnik na intervalu od $0$ do $100 cm$ predočuje da $12$ rijeka ima vodostaj niži od $100 cm,$ a primjerice pravokutnik na intervalu od $501$ do $600 cm$ predočuje da $4$ rijeke imaju visinu vodostaja veću od $501 cm$ i manju od $600 cm .$

Koliko je rijeka u toj regiji?
Koliko cm treba biti vodostaj da bi se proglasile izvanredne mjere ili izvanredno stanje obrane od poplave ako znamo da za $58$ rijeka nisu proglašene ni izvanredne mjere ni izvanredno stanje.

Zbrojimo sve visine stupaca, tj. brojeve rijeka na svakom intervalu. Rijeka u toj regiji ima $86 .$
Zbrojimo visine prvih $5$ stupaca, $12 + 6 + 8 + 18 + 14 = 58 .$ Visinu vodostaja do $500 cm$ ima $58$ rijeka, znači vodostaj treba biti $501 cm$ da bi se proglasile izvanredne mjere zaštite od poplave.

Zatvori

Zanimljivost

Zadatci s analizom podataka često se pojavljuju na državnoj maturi pa predlažemo da pogledate i ove zadatke:

Državna matura, ljetni rok šk. god. 2014./2015., Matematika, osnovna razina B, zadatak 16.

Državna matura, ljetni rok šk. god. 2013./2014., Matematika, osnovna razina B, zadatci 26. i 28.

Jezero	Dubina u metrima
Vransko jezero na Cresu	$74$
Peruća	$64$
Prokljansko jezero	$25$
Lokvarsko jezero	$40$
Sabljačko jezero	$6$
Bajersko jezero	$7$
Baćinska jezera	$32$

Aktivnosti za samostalno učenje

Na početku...

Riješite, provjerite i podijelite

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Kolekcija zadataka 2

Zadatak 3.

Zadatak 4.

Projekt

Zadatak 5.

Projekt

Zadatak 6.

Kutak za znatiželjne

Kolekcija zadataka 3

Zadatak 7.

Zadatak 8.

Zadatak 9.

Zanimljivost

...i na kraju

Zadatak 10.