

Kolika je cijena jedna olovke?
Jednadžbe
dobivene u animaciji čine
Pomoć:
Zapisane jednadžbe su oblika
Cijenu jedne olovke označili smo nepoznanicom , a cijenu jedne gumice nepoznanicom .
Pomoć:
U sustavu dviju linearnih jednadžbi s dvije nepoznanice
nepoznanice su označene slovima
i
Da bismo saznali cijenu olovke i gumice, moramo riješiti sustav.
Pomoć:
Riješiti sustav znači izračunati vrijednost nepoznanice
i
Postupak:
Sustav riješite metodom suprotnih koeficijenata
tako da pomnožite drugu jednadžbu s
Cijena jedne olovke iz animacije je
Pomoć:
Cijena olovke označena je nepoznanicom
koju pišemo u prvom članu uređenog para.
Za uvježbavanje postavljanja i rješavanja sustava dviju linearnih jednadžbi s dvije nepoznanice predlažemo nekoliko zadataka koje možete samostalno riješiti u bilježnicu ili u nekom interaktivnom elementu. Posljednjih nekoliko zadataka je za one koji žele znati više, ali svi ih možete pokušati riješiti. Nakon što riješite zadatke, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili zamolite da vam pomognu ako vam je neki zadatak težak.
Provjerite je li uređeni par
rješenje sustava
Uređeni par
je rješenje sustava ako ga uvrstimo u jednadžbe i dobijemo točnu jednakost za obje jednadžbe.
Uređeni par
je rješenje sustava.
Provjerite je li uređeni par rješenje sustava
Uređeni par rješenje sustava.
Pomoć:
Uređeni par je rješenje sustava ako je rješenje obiju jednadžbi.
Metodom supstitucije riješite sustav dviju linearnih jednadžbi s dvije nepoznanice.
Iz druge linearne jednadžbe izrazimo nepoznanicu
Dobiveni izraz uvrstimo u prvu jednadžbu:
Dobivenu vrijednost nepoznanice
uvrstimo u
Rješenje je uređeni par
Metodom suprotnih koeficijenata riješite sustav dviju linearnih jednadžbi s dvije nepoznanice.
Uočimo suprotne koeficijente uz nepoznanice
Uvrstimo
u prvu jednadžbu:
Rješenje sustava je uređeni par

učenika Osnovne škole Smiljane išla su na izlet u Zagreb. Smješteni su u trokrevetnih i četverokrevetnih soba. Dječaci su smješteni u četverokrevetne, a djevojčice u trokrevetne sobe. Zapišite sustav dviju linearnih jednadžbi s dvije nepoznanice s pomoću kojih možemo saznati koliko je učenika, a koliko učenica na izletu u Zagrebu.
Odaberite točan odgovor.
Pomoć:
Označimo s
broj učenika, a s
broj učenica. Njihov zbroj je
Učenike treba podijeliti u četverokrevetne sobe i tome pribrojiti učenice podijeljene u trokrevetne sobe. Kad zbrojimo broj soba u kojima su učenici s brojem soba u kojima su učenice, dobijemo ukupan broj soba.
Melita i Andreja zajedno imaju
godine. Melita je četiri godine starija od Andreje. Koliko je godina Meliti, a koliko Andreji?
Označimo s broj Melitinih godina, a s broj Andrejinih godina. Kad podatke zapišemo u obliku sustava dviju linearnih jednadžbi s dvije nepoznanice, vidimo da je:
Pri rješavanju sustava metodom supstitucije, uvrstimo izraz za nepoznanicu iz druge jednadžbe u prvu i dobijemo
Uvrstimo u drugu jednadžbu i dobijemo vrijednost nepoznanice
Meliti su godine, a Andreji godina.

Osmislite nekoliko problemskih zadataka. Pretvorite ih u QR kodove. To možete učiniti vrlo jednostavno kopirajući svoje zadatke u prazno polje na ovoj stranici, a preuzeti ih na svoje računalo klikom na gumb Download. Ispišite QR kodove i rasporedite ih po učionici, školskom hodniku, školskom igralištu ili na nekom drugom prostoru. Pronađite jednu od besplatnih aplikacija za čitanje QR kodova i preuzmite je na mobitele. Podijelite se u skupine tako da u svakoj skupini bude jedan mobitel ili tablet s čitačem QR kodova. Organizirajte natjecanje u kojem će učenici tražiti QR kodove koje je sakrila nastavnica ili protivnička skupina. Nagradite skupinu koja je najbrže pronašla i riješila sve zadatke.
Na jednom natjecanju bilo je
zadataka. Za svaki točan odgovor dobivalo se
bodova, a za svaki netočan odgovor gubila su se
boda. Ana je osvojila
boda.
Koliko je zadataka Ana riješila točno, a koliko netočno, ako je riješila sve zadatke?
Pomoć:
Opseg pravokutnika je Ako duljinu jedne stranice pravokutnika povećamo za a duljinu druge stranice smanjimo za pravokutnik će postati kvadrat. Kolike su početne stranice pravokutnika?
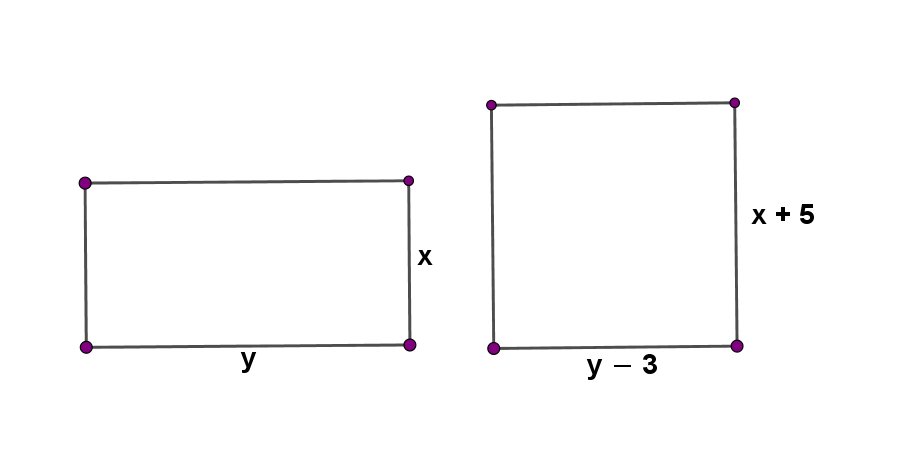
Označimo s i duljine stranica pravokutnika.
Iz formule za opseg vrijedi:
Ako duljinu jedne stranice povećamo za a drugu smanjimo za pravokutnik postaje kvadrat, odnosno duljine stranica bit će mu jednake. Zapišemo li to jednadžbom, dobijemo:
Zapišimo te dvije jednadžbe u sustav dviju linearnih jednadžbi s dvije nepoznanice i riješimo sustav:
Uvrstimo dobiveni
u jednu od jednadžbi:
Duljine stranica pravokutnika su i
Pomičući elemente mišem i spajajući sustave s rješenjima, složite tangram. Elemente možete i rotirati mišem, pomičući točku označenu na svakom elementu.
Primjer 1.
Riješimo sustav dviju jednadžbi s dvije nepoznanice
uz uvjet da su i
Ovaj sustav jednadžbi nije jednostavno riješiti uobičajenim metodama. Da bismo pojednostavnili ovaj sustav, jednadžbi uvodimo nove nepoznanice i takve da je i
Sada riješimo pomoćni sustav
s nepoznanicama i bilo kojom metodom.
Kako je
i
uvrstimo dobivena rješenja za
i
i dobijemo
Rješenje sustava je uređeni par
Provjerimo je li uređeni par
rješenje sustava dviju jednadžbi s dvije nepoznanice:
Uvrstimo vrijednosti nepoznanica
i
u prvu jednadžbu.
Zatim uvrstimo te vrijednosti u drugu jednadžbu.
Uređeni par je rješenje sustava.
Ovakav način rješavanja sustava dviju jednadžbi nazivamo metodom uvođenja nove nepoznanice. Ako uočimo pravilnost u obje jednadžbe, na taj način možemo pojednostavniti rješavanje sustava.
Riješite sustav dviju jednadžbi s dvije nepoznanice:
uz uvjet da su i Dobiveno rješenje provjerite.
Prisjetimo se da je
i
Pojednostavnimo rješavanje sustava tako da uvedemo nove nepoznanice:
i
Dobijemo pomoćni sustav
koji možemo riješiti bilo kojom metodom.
Rješenje pomoćnog sustava je
i
Iz toga slijedi i odnosno rješenje početnog sustava je uređeni par
Za provjeru, uvrstimo vrijednosti nepoznanica najprije u prvu jednadžbu, pa u drugu jednadžbu.
Uređeni par je rješenje sustava.
Zadaci sa sustavima dviju linearnih jednadžbi s dvije nepoznanice često se pojavljuju na Državnoj maturi pa predlažemo da pogledate i sljedeće zadatke:
Za kraj, odigrajte igru u razredu. Podijelite se u parove. Svaki učenik neka smisli jednu linearnu jednadžbu s dvije nepoznanice i zapiše je na papirić. Zamijenite papiriće s drugim učenicima u razredu. U paru zapišite dvije dobivene jednadžbe u sustav i riješite ga metodom po želji. Provjerite dobiveno rješenje. Izložite sustave i rješenja svih parova na panou u učionici. Sva rješenja ucrtajte u isti koordinatni sustav u ravnini.