

U sljedećim primjerima bavit ćemo se crtanjem i konstrukcijom pravilnih mnogokuta.
Geometrijsko crtanje je postupak u crtanju pri kojem upotrebljavamo dva trokuta, šestar, kutomjer i ostali geometrijski pribor.
Geometrijska konstrukcija je postupak crtanja pri kojem se koristimo samo šestarom i ravnalom.
Konstruirajte na papiru jednakostranični trokut ako mu je duljina stranice
Nacrtaj na papiru kvadrat ako mu je duljina stranice
Podjela kružnice na jednake dijelove bila je vrlo važna za pitagorejce (koji su tvrdili da broj postoji u svakoj pojavi svijeta) te je poslije našla primjenu u konstrukciji pravilnih mnogokuta.
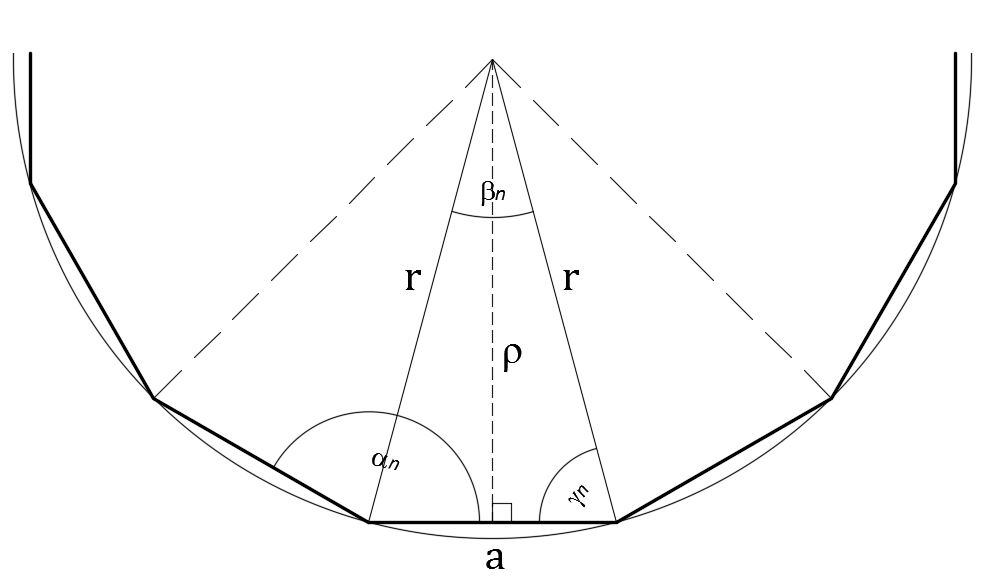
Pravilni mnogokut možemo nacrtati, odnosno konstruirati na razne načine, ovisno o tome koji je element zadan. Da bismo to mogli učiniti, potrebno je analizirati njegov karakteristični trokut.
Mi ćemo navesti dva osnovna načina crtanja i konstrukcije pravilnih mnogokuta, a to su:
Primjer 1.
Konstruirajmo pravilni šesterokut ako mu je duljina polumjera opisane kružnice
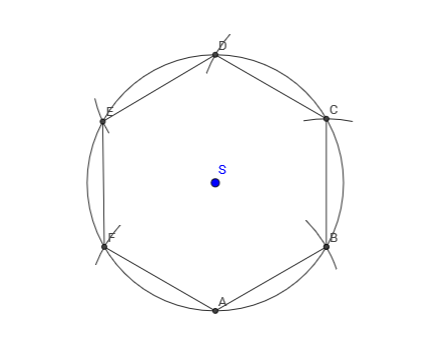
Središnji kut pravilnog šesterokuta iznosi
To znači da je karakteristični trokut jednakostraničan i da su stranice šesterokuta jednake duljine, kao i polumjer opisane kružnice.
Opis konstrukcije:
Konstruirajte na papiru jednakostranični trokut ako mu je duljina polumjera opisane kružnice
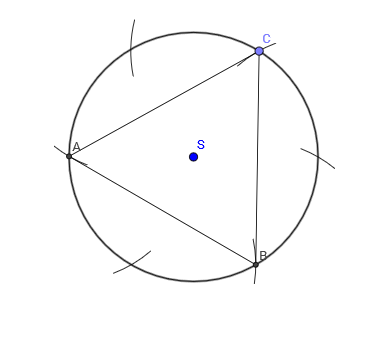
Središni kut pravilnog trokuta iznosi
Opis konstrukcije:
Konstruirajte na papiru pravilni dvanaesterokut ako mu je duljina polumjera opisane kružnice
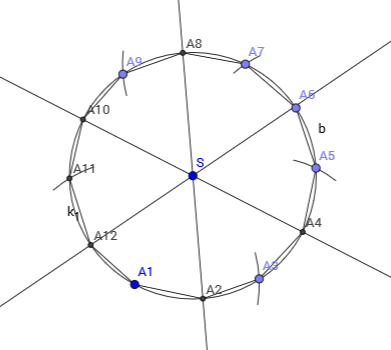
Središnji kut pravilnog dvanaesterokuta iznosi
Opis konstrukcije:
Primjer 2.
Konstruirajmo pravilni četverokut ako mu je duljina polumjera opisane kružnice
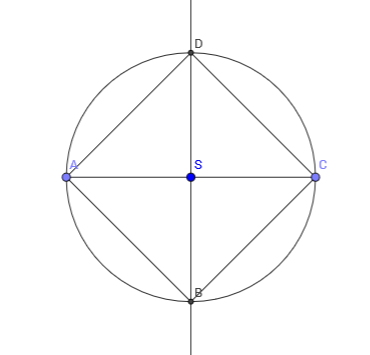
Središnji kut pravilnog četverokuta iznosi
Konstruirajte na papiru pravilni osmerokut ako mu je duljina polumjera opisane kružnice
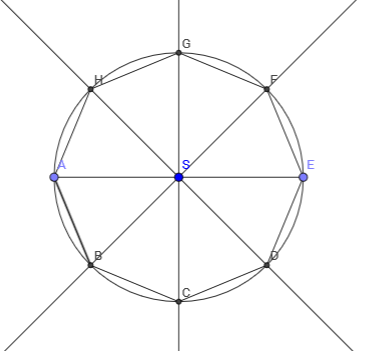
Središnji kut pravilnog osmerokuta iznosi
Opis konstrukcije:
Primjer 3.
Nacrtajmo pravilni peterokut ako mu je duljina polumjera opisane kružnice
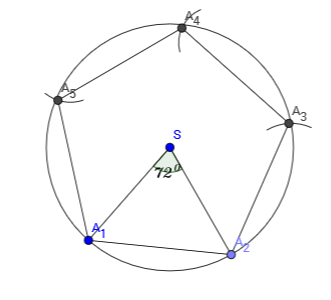
Središnji kut pravilnog peterokuta iznosi
Opis crtanja:
Odredimo sjecišta kružnice i krakova središnjeg kuta.
Dobivenu tetivu nanesemo po kružnici.
Tako dobivene točke su vrhovi pravilnog peterokuta.
Spojimo sve međusobno susjedne vrhove.
Nacrtajte na papiru pravilni deveterokut ako mu je duljina polumjera opisane kružnice
Središnji kut pravilnog deveterokuta iznosi
Crtajte kao i u crtanju pravilnog peterokuta.
Primjer 4.
Nacrtajmo pravilni peterokut ako mu je duljina stranice
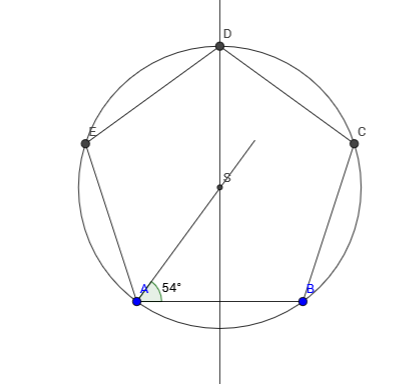
Izračunajmo veličine kutova karakterističnog trokuta:
Opis konstrukcije:
Koji pravilni mnogokut ima duljinu stranice jednake duljine kao i polumjer opisane kružnice?
Pomoć:
Izračunajte kutove karakterističnog trokuta.
Postupak:
Matematičari su vrlo dugo tražili metode konstruiranja pravilnog sedmerokuta, deveterokuta i jedanaesterokuta. Potkraj 18. stoljeća tada 19-godišnji njemački matematičar Karl Friedrich Gauss dokazao je da se ne mogu konstruirati.