

Ponovimo!
Pojam potencije
Ako je realan broj, a prirodan broj, onda je
Broj je baza, a broj je eksponent potencije
Pravila za računanje s potencijama
Pojam imaginarne jedinice
Ponovimo računanje s potencijama u nekoliko zadataka.
jednako je:
jednako je:
Kvadrat imaginarne jedinice jednak je:
jednako je:
jednako je:
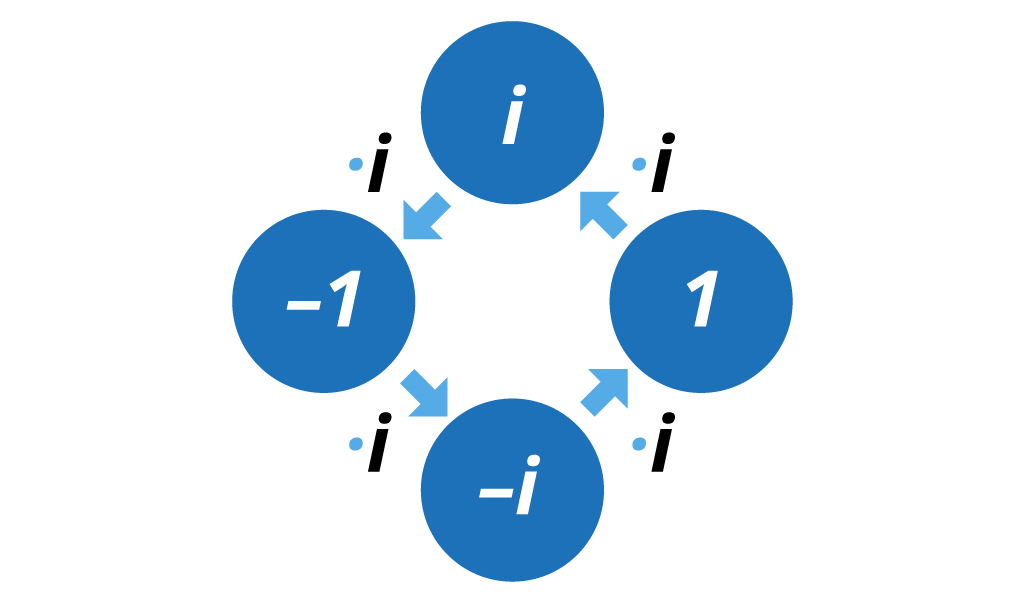
Pogledajmo kako su potencije broja
smještene na brojevni pravac.
Potencije broja
sa slike pridružite točki A ili B.
Primijetimo pravilnost vezanu za eksponent potencije broja
Ako je eksponent neparan broj, potencija je jednaka
a ako je eksponent paran broj onda je potencija
Pri množenju imaginarne jedinice brojevima , možemo primijetiti još jedno zanimljivo svojstvo:
Primjer 1.
Primjer 2.
Pogledajmo kako tu pravilnost pri potenciranju imaginarne jedinice možemo iskoristiti.
Vrijednosti ponavljaju se u potenciranju imaginarne jedinice.
To ćemo ponavljanje iskoristiti da bismo mogli potencirati imaginarnu jedinicu i kada su eksponenti brojeva veći od
Uočimo da smo već u primjeru upotrijebili
Za potencije imaginarne jedinice vrijedi:
gdje je cjelobrojni rezultat dijeljenja eksponenta s brojem a je ostatak pri tom dijeljenju i može biti jedan od brojeva iz skupa
Primjer 3.
Izračunajmo
Primjenimo sada svojstva potencija uz
Izračunajte, pa provjerite.
Koristeći se Generatorom zadataka možete vježbati potenciranje imaginarne jedinice uz mogućnost provjere rješenja. Puno uspjeha!
Kao rezultat zbrajanja, oduzimanja, množenja i potenciranja kompleksnih brojeva možemo dobiti realni broj.
Svaki realan broj ujedno je kompleksni, s imaginarnim dijelom jednakim
Izračunajmo imaginarni dio broja
Zaključak je: Im