


Zašto meljemo kavu? Jeste li kada razmišljali o tome? Zašto jednostavno ne ubacimo u vodu zrnca kave i skuhamo je? Vjerojatno bi nas prošla volja za kavom dok bi se bilo što dogodilo.
Zašto često sitnimo šećer, pogotovo kada pripremamo kolače? Napravite šlag s konzumnim bijelim šećerom i šećerom u prahu. Osjetite li razliku?
Zašto se naša krv sastoji od bilijuna crvenih i milijarde bijelih krvnih zrnaca, koji čine litara krvi? Njihova je zadaća da raznose kisik po cijelom tijelu. Upijaju i otpuštaju kisik, odnosno izmjenjuju ga s ugljikovim dioksidom iz stanica, i to samo svojom površinom. Dakle, što su manja, ima ih više (za isti volumen) te time bolje ispunjavaju svoju zadaću.
Primjer 1.
Zamislimo da su nam sva crvena krvna zrnca, kojih u ljudskom organizmu ima oko litre, u jednoj kugli.
Koliki je promjer takve kugle?
Koliko je približno oplošje te kugle?
Umjesto velike kugle, imamo
bilijuna
malenih krvnih zrnaca. Zamislimo da su u obliku kuglica. Koliko je ukupno oplošje tih krvnih zrnaca?
Koliko je oplošje jednoga crvenoga krvnog zrnca u obliku valjka?
Koji je odnos oplošja raspršenih krvnih zrnaca u obliku valjka u usporedbi s oblikom kugle?
Općenito, ako se tijelo raspadne na
dijelova, tada je povećanje oplošja približno jednako kubnom korijenu broja
tj.
pri čemu je
oplošje jednog tijela, a
ukupno oplošje svih raspršenih čestica. Dokažite formulu.
Koristite se poznatim proporcijama za stranice nekog tijela, odnosno njihova oplošja i obujme: i
Dokaz možete provesti s pomoću formule za oplošje i obujam kugle ili valjka uz uvjet:
Izjednače se obujmi jednog tijela, i raspršenih tijela,
Dobije se da je omjer stranica (polumjera) tijela koje promatramo jednak
Usporedimo pripadajuća oplošja i dobiveni kvadrat omjera stranica (polumjera) zamijenimo s Sredimo izraz i dobijemo traženu formulu.
Npr. za kuglu vrijedi:
Pokušajte sami s formulama za valjak.
Provjerite formulu za crvena krvna zrnca iz prethodnog primjera.
Uzmimo u obzir pogrešku zaokruživanja pri računanju.
Sami provjerite za oblik valjka.
Sada možemo razumjeti zašto neke tvari usitnjavamo. To činimo da bismo dobili veću površinu materije na kojoj djeluje neko svojstvo.
U prethodnom nam je primjeru cilj bio za isti obujam dobiti što veće oplošje.
Pogledajmo sada obrnuti primjer, tzv. problem konzerve.

Problem konzerve
Kako napraviti valjkastu posudu s dnom i poklopcem tako da njezino oplošje uz zadan obujam
bude što manje?
Odnosno, proizvođače zanima kako utrošiti što manje materijala (lima) za jedno pakiranje?
Diferencijalnim računom (koji vi još ne znate) može se dokazati da je oplošje minimalno ako je osni presjek valjka kvadrat. Međutim, pogledate li u ostavu, hladnjak ili neko slično mjesto u kuhinji, vidite da su uglavnom limenke više nego što je promjer dna. Provjerimo zašto je tako.
Pri rezanju plašta za konzervu nema otpada. Međutim pri rezanju dna i poklopca obično ostaje dio od kruga. Dakle, za minimalizaciju troškova treba uzeti u obzir da se za svako dno i poklopac izreže kvadrat (ili neki drugi mnogokut) u kojem izrezujemo krug, dno konzerve, zato uključimo otpad u izračun. Za sada ne možemo izračunati kada će to biti najpovoljnije, ali možemo pronaći nekoliko limenki i mjeriti.
Pronađite limenke istog obujma, ali različitih veličina. Uzmite metar te izmjerite potrebne veličine za računanje oplošja i obujma. Usporedite limenke istog obujma. Pokušajte odgovoriti na pitanje u kojem su omjeru visina konzerve i promjer dna. Dobivate li slične rezultate?
Omjer bi trebao biti približno jednak
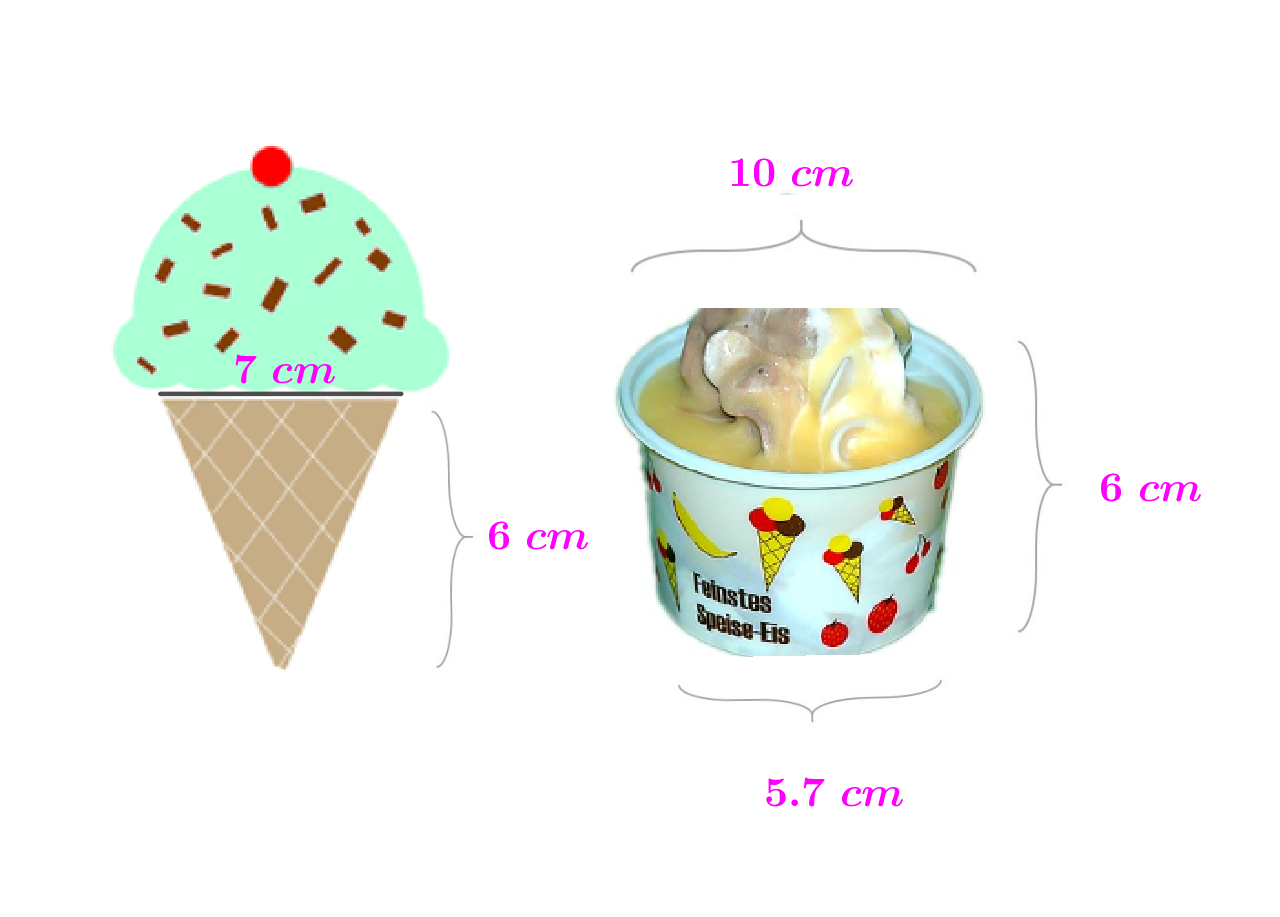
U ovaj vrući dan odlučili ste nakon škole otići na sladoled. U slastičarnici možete birati želite li sladoled u čašici ili kornetu. Cijena im je jednaka. Netko je naručio u čašici, a netko u kornetu. Čašica je bila napunjena sladoledom do vrha, a kornet je bio pun i imao kuglicu sladoleda u obliku polukugle još iznad korneta. Tko je dobio više sladoleda za jednaku cijenu? Mjere pročitajte sa slike.
Za kornet izračunajte obujam stošca visine i promjera te mu dodajte obujam polukugle promjera
Čašica ima oblik krnjeg stošca promjera baza i te visine
Bolje su prošli oni koji su naručili sladoled u čašici.
Ilirske gomile grobovi su poglavica rodova i plemena te uglednih ljudi iz ilirskih plemena na području Dalmacije i Hercegovine. To su gomile kamenja nabacanih u obliku krnjeg stošca. Veličina gomile ovisila je o brojnosti roda ili plemena iz kojeg pokojnik potječe.
Megalitička kultura jedna je od najdužih i najrasprostranjenijih graditeljskih kultura u povijesti. Nastala je na početku ljudske povijesti, oko 3 800 g. pr. Krista, i trajala tri tisućljeća. Tri su osnovne vrste megalita. Jedna su vrsta golemi kameni blokovi, najčešće valjkastoga, stožastoga ili vretenastog oblika.
Istražite više o ostavštini megalitičkih građevina. Jesu li se u prošlosti koristili još neki geometrijski oblici? Jesu li ih ljudi pronalazili u prirodi ili oblikovali, klesali, rezbarili i slično?
Zašto su ih gradili i kako su uspjeli obrađivati tako goleme blokove? Pronađite najpoznatije megalite u svijetu.

Prerađivači papira kupuju drva od šumarskih poduzeća. Ako im je prodano debla promjera i duljine koliko su kubika drva kupili? (Pod kubik se podrazumijeva kubni metar.)

Istražite koliko se šume uništi za proizvodnju papira. Što država i lokalne zajednice poduzimaju u vezi s tim? Kako vi sudjelujete u smanjenju uništavanja šuma? Organizirajte se s razrednikom i provedite malu akciju skupljanja papira. Povežite skupljeni papir u oblik kocke ili smotajte u valjak te izračunajte njegov obujam. Izmjerite masu tih blokova pa izračunajte gustoću skupljenog papira.
Posjetite ustanove u svojemu mjestu koje se bave otkupom papira, to jest imaju reciklažna dvorišta. Zamolite stručnjake da vam održe kratku edukaciju o čuvanju naših šuma, o odvajanju otpada i trenutačnom stanju u vašemu mjestu. Koliko su vaši sugrađani senzibilizirani o uništavanju našeg planeta? Pokušajte utjecati pozitivno u svojoj okolini na odvajanje otpada i odvoženje u recikliražna skladišta.
Bilježite kojom ste se matematikom i s koliko nje koristili u ovom projektu. Napravite s nastavnicima i ostalim učenicima u školi prezentaciju o svojim saznanjima.

Kako su dani postali topliji, teta Marija odlučila je napuniti svoj bazen u dvorištu. Bazen je cilindričnog oblika promjera Puni se s pomoću cijevi koja u jednom satu ispusti vode. Koliko je bazen dubok ako se tom brzinom za pet sati napuni četvrtina bazena?
Koliko je
vode u kubnim metrima?
Dubina bazena iznosi:
Koja geometrijska tijela nastaju rotacijom sljedećih ravninskih likova (kao u interakciji u nastavku):
Izračunajte njihova oplošja i volumene.
Uputa za uporabu interakcije: nakon svakog zadatka osvježite interakciju (oznaka u gornjem desnom kutu lijevog prozora) kako biste obrisali trag koji ostavlja geometrijski lik rotacijom oko svoje osi.
Opustite se na posljednjim satovima Matematike uz timski rad.
Pripremite neko geometrijsko tijelo koje nađete kod kuće (može i u školi) i donesite ga na sat. Tijelo mora biti izmjerljivo. Pripremite se za mjerenje. Na satu nasumično birate tim kojem ćete dati svoje geometrijsko tijelo. Dakle, razmijenite stvari geometrijskog oblika, ali tako da prije sata nitko ne zna što će dobiti za rad. Podijelite uloge u timu i prionite poslu. Istražite geometrijsko tijelo koje ste dobili, izmjerite, utvrdite koje vam formule trebaju i izračunajte što više elemenata iz toga geometrijskog oblika. Sastavite priču o tijelu. Zamislite da ga možete iskoristiti na neki način, napuniti nečim, usporediti ili nešto treće. Napravite prezentaciju o svojemu malome projektnom zadatku.
Ideju potražite u Swayu
, Geometrijska tijela oko nas, od učenika SŠ Markantuna de Dominisa Rab, koji su radili nešto slično.