

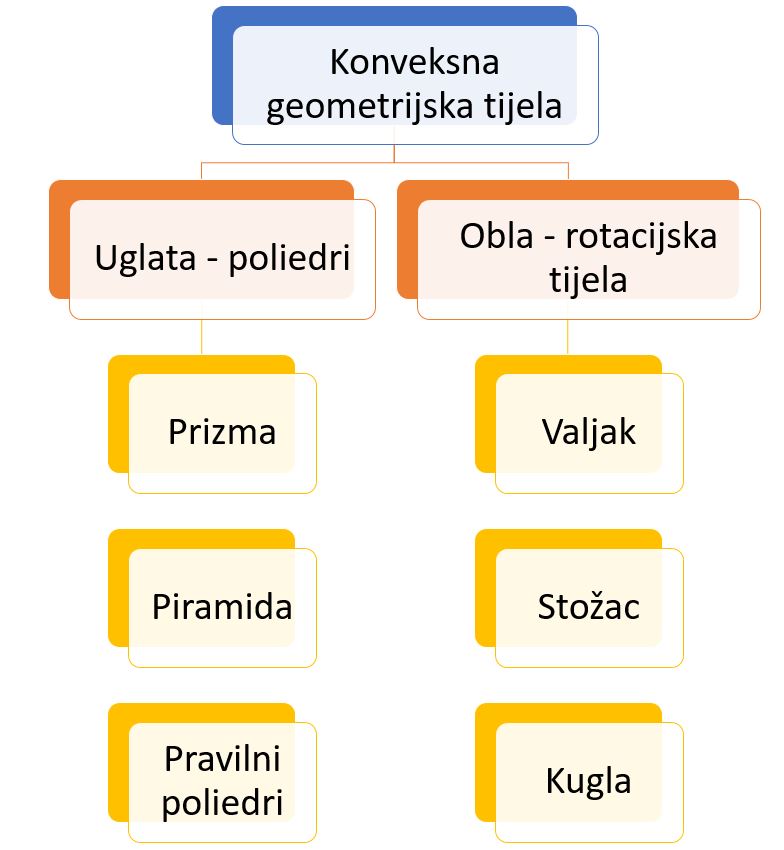
Konveksno geometrijsko tijelo je omeđeni dio prostora čije spojnice bilo kojih dviju njegovih točaka pripadaju tom tijelu.
Rotacijska tijela su tijela koja nastaju rotacijom krivulje (geometrijskog lika) oko zadane osi rotacije.
Pogledajte u sljedećoj interaktivnoj vježbi što se događa s pravilnom
-terostranom prizmom kojoj povećavamo broj bridova baze (pravilnog mnogokuta). U lijevom prozoru s pomoću klizača mijenjajte veličinu brida
i broj bridova
U desnom prozoru možete mijenjati visinu prizme pomicanjem gornje baze. Cijelu prizmu možete horizontalno pomicati pomicanjem baze (mnogokuta) u lijevom prozoru. Smanjite veličinu brida baze, a povećajte broj bridova do maksimuma. Što ste dobili? Na što vas podsjeća dobiveno geometrijsko tijelo?
Ponovimo definiciju prizme.
Prizma je geometrijsko tijelo omeđeno s -terokuta koje nazivamo i s paralelograma, prizme. Sve pobočke zajedno čine prizme.
Promatrajući prethodnu interakciju intuitivno možemo zaključiti da za jako veliki
i zanemarivo malu duljinu stranice
naš mnogokut „postajeˮ krug te plašt više nema bridove, nego postaje valjkasta ploha. Prizma se pretvara u novo geometrijsko tijelo koje nazivamo valjak. Pogledajmo interakciju.
Prema analogiji s prizmom definirajmo valjak.
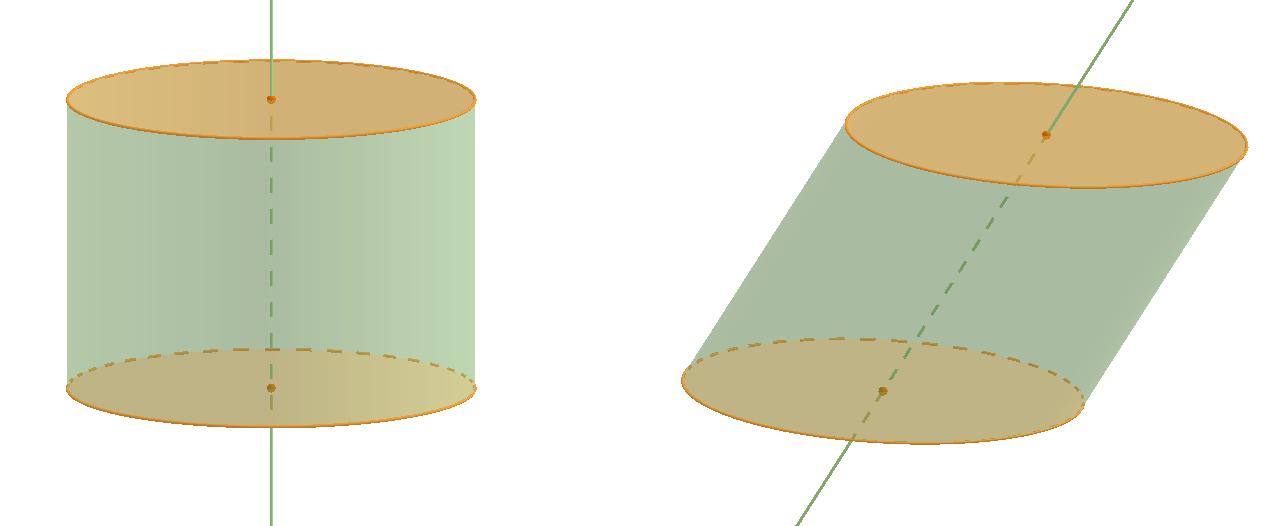
Valjak je najmanji konveksni skup koji sadržava dva paralelna sukladna kruga.
Valjak je geometrijsko tijelo omeđeno s
Neka su zadane jedna dužina i elipsa. Elipsa je određena dvama žarištima udaljenima od središta elipse za duljinu Postavimo li jednu krajnju točku dane dužine u središte elipse, a elipsu pomičemo danom dužinom, dobiveni skup točaka u prostoru nazivamo valjak. Polumjeri elipse jesu polumjeri valjka. Dana dužina jest izvodnica valjka, a udaljenost između dviju najudaljenijih dobivenih elipsa jest visina valjka. Elipsa sa središtem u početnoj točki izvodnice naziva se baza valjka. Skup točaka svih elipsa bez početne i završne (elipse sa središtem u krajevima dane dužine) nazivamo plašt valjka. Ako je baza elipsa, valjak nazivamo eliptični, a ako je krug, valjak je kružni.
U sljedećoj interakciji konstruirajte valjak pomičući točku po danoj dužini – izvodnici. Možete mijenjati udaljenost žarišta od središta elipse,
Ako su njihove udaljenosti jednake nuli, elipsa postaje kružnica. Možete mijenjati i veličinu elipse, odnosno polumjer kružnice,
Poigrajte se interakcijom i istražite mogućnosti koje ona nudi.
U animaciji pogledajte kako nastaje valjak, odnosno što čini mrežu valjka.
Dan je uspravan valjak visine
i polumjera baze
Odgovorite na sljedeća pitanja o mreži valjka. Ako za neko pitanje niste sigurni u odgovor, još jedanput pogledajte animaciju.
Baza je , a plašt je .
Na prazne crte, odnosno iza jednakosti posložite ponuđene izraze.
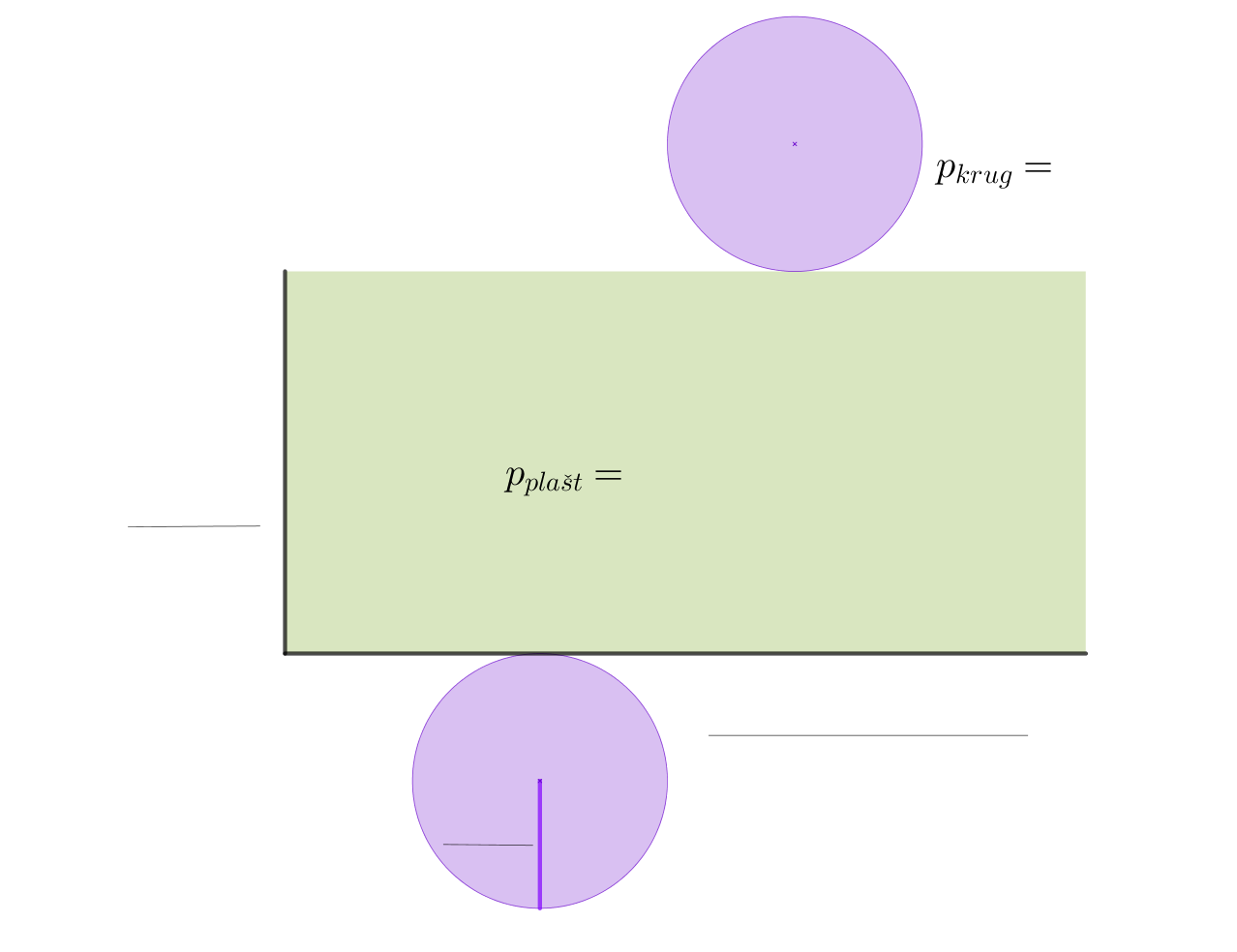
Površinu baze (kruga) označit ćemo s
Površinu plašta (pravokutnika) označit ćemo s
Pokušajte sami napraviti mrežu valjka. Nakon što ste pripremili pravokutnik čija je jedna stranica jednaka duljini kružnice, nacrtajte najkraći put između dviju najudaljenijih točaka pravokutnika. To je njegova dijagonala. Nakon što mrežu savijete u valjak, pogledajte putanju najkraćeg puta. Istražite više o toj spojnici koju nazivamo zavojnica ili cilindrična spirala. Više zanimljivosti potražite u matematičkom časopisu MiŠ (br. 18/2013.).
Presijecite valjak ravninom koja sadržava os valjka. Nacrtajte taj presjek.
Koji geometrijski lik dobijemo kada valjak presječemo ravninom koja sadržava os valjka, odnosno promjere krugova baze?
Takav presjek nazivamo osni presjek.
Je li presjek isti geometrijski lik ako je valjak uspravan ili kos?
Koji je osni presjek moguć ako je valjak uspravan?
(Moguće je više odgovora.)
Valjak kojem je osni presjek kvadrat naziva se jednakostraničan valjak.
Pogledajte osni presjek kosog valjka (paralelogram) u sljedećoj interakciji.
Uočite kada je kut izvodnice i promjera baze valjka (šiljasti kut paralelograma) najmanji. Odaberite alat za pomicanje te pomičite označenu točku i promatrajte kako se mijenja taj kut. U kojem je položaju ravnina osnog presjeka u odnosu prema ravnini baze valjka kada je kut presjeka najmanji? U kojem se položaju dobije pravi kut?
Pokušajte sada odgovoriti na sljedeća pitanja o osnom presjeku valjka.
Jesu li svi osni presjeci sukladni?
Ako je osni presjek (paralelogram) okomit na ravninu baze, njegov je pripadajući manji kut:
Osni presjek kojem izvodnica s bazom zatvara najmanji kut naziva se karakteristični presjek valjka.
Može li se dobiti kao osni presjek pravokutnik?
U kojem su položaju ravnine koje sadržavaju karakteristični presjek valjka i osni presjek kojem je izvodnica okomita na promjer?
Iz valjka polumjera
izvađen je valjak polumjera
(sa zajedničkim središtem baza). Manjem je valjku osni presjek
Izračunajte osni presjek i površinu baze šupljeg valjka.
Osni presjek velikog valjka iznosi pa je osni presjek šupljeg valjka
Površina baze je površina kružnog vijenca:
Kosom valjku karakterističan je presjek romb stranice
i šiljastog kuta
Izračunajte visinu kosog valjka te površinu baze.
Kojom formulom računamo oplošje prizme kojoj je površina baze
te površina plašta
Prisjetite se interakcije u kojoj smo od prizme dobili valjak. Što znamo o njihovim oplošjima?
Vrijedi li ista formula za oplošje valjka?
Neka je površina baze četverostrane pravilne prizme stranice i visine površina baze valjka polumjera i visine te površine plašta prizme, odnosno valjka. Uparite točne izraze.
|
|
|
|
|
|
|
|
|
|
|
|
Za razliku od prizme, valjak uvijek
ima
istu bazu pa je zato i formula za računanje oplošja ista za svaki valjak. Uvrštavanjem prethodnog izraza u formulu za oplošje
dobije se formula za računanje oplošja valjka.
Oplošje uspravnog valjka polumjera baze i visine jednako je
Primjer 1.
Izvedimo formulu za oplošje jednakostraničnog valjka ako imamo zadan polumjer baze
Jednakostraničnom valjku osni je presjek kvadrat pa vrijedi U formuli za oplošje valjka prikažimo s pomoću
Oplošje jednakostraničnog valjka za dani računamo formulom:
Izvedite formulu za oplošje jednakostraničnog valjka ako je zadana visina valjka
Dovoljno je u formulu dobivenu u prethodnom primjeru uvrstiti
Za dane elemente valjka potražite pripadajuća rješenja.
Odredite visinu uspravnog valjka ako je površina baze
, a oplošje
.
Neka je jednakostraničnom valjku površina baze jednaka . Izračunajte oplošje valjka.
Koliko je oplošje valjka kojem je promjer baze i visina
Jednakostraničnom valjku površina je osnog presjeka Izračunajte oplošje valjka.
Uspravni valjak s promjerom baze ima oplošje Koliko je visok valjak?
Prema analogiji s obujmom prizme, izvest ćemo formulu za obujam valjka.
Kojom formulom računamo obujam prizme kojoj je površina baze te visina

Stari Babilonci i Egipćani su obujam valjka računali približno. Točnu formulu za obujam, te za površinu plašta, prvi je izračunao Arhimed.
Dokažite formulu za obujam valjka u tri koraka.
(tekst: formula
)
Obujam valjka polumjera baze i visine jednak je
Odredite obujam jednakostraničnog valjka ako mu je polumjer baze
Izračunajte obujam i oplošje jednakostraničnog valjka visine
Za jednakostranični valjak vrijedi:
U sljedećoj interakciji odredite nepoznati element valjka s pomoću formule za obujam valjka. U svakom zadatku izračunajte i oplošje valjka.
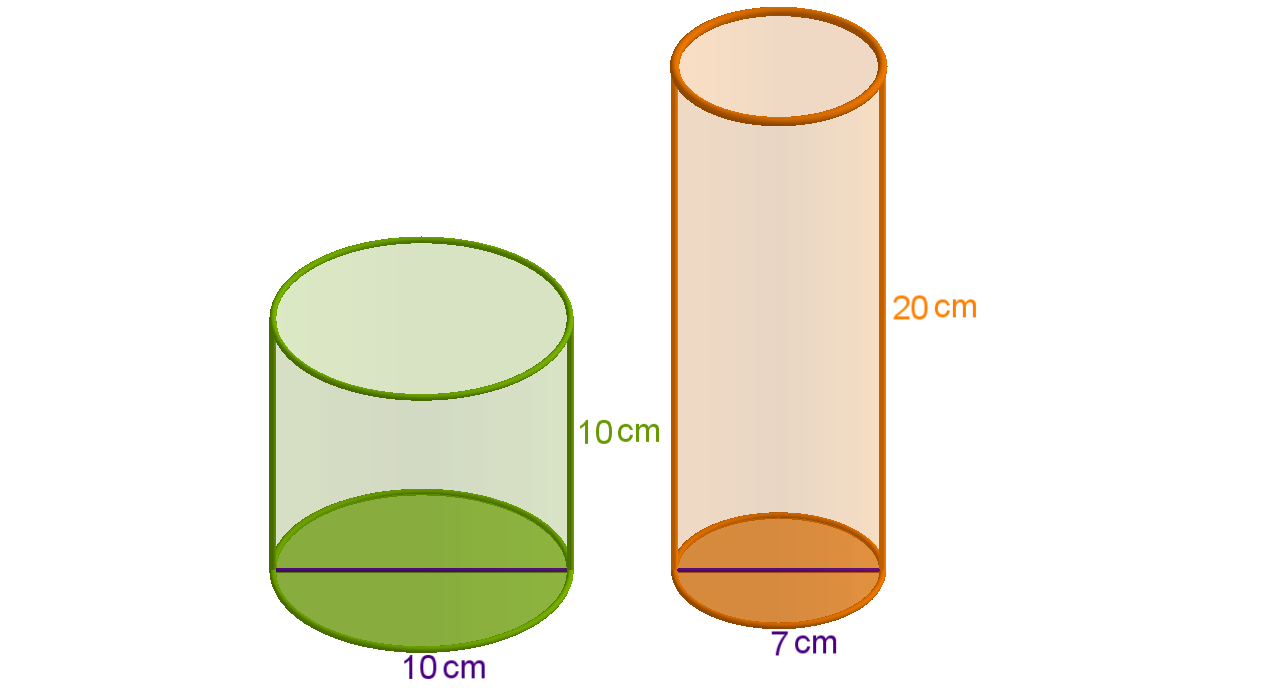
U koju posudu stane više tekućine?
Želite posude oblijepiti reklamnom folijom. Za koju će posudu biti potrebno više folije?
Pomoć:
Polumjer većeg podmetača iznosi a manjeg i visina im je
Koja je količina stiropora potrebna za oba podmetača?
Pomoć:
Pripazite na mjerne jedinice!

Znate li što je stiropor ili ekspandirani polistiren? S nastavnicima kemije istražite svojstva tog materijala koji je u posljednje vrijeme popularan kao dobar izolacijski materijal, posebno za vanjske zidove zgrada. Je li ekološki prihvatljiv materijal? Istražite je li i vaš stambeni prostor toplinski izoliran. Koja se debljina stiropora preporučuje s obzirom na namjenu i eventualno podneblje u kojem živite?
Potražite vanjske stručnjake i zatražite od njih da vam u školi održe predavanje o primjeni stiropora, energetskoj učinkovitosti i ekološkoj prihvatljivosti tih materijala.

Jeste li uočili reklame izrađene od stiropora? Potražite na internetu ideje i sami izradite geometrijske oblike s pomoću stiropora, s unaprijed zadanim dimenzijama. Pokažite svoju kreativnost u povodu obilježavanja nekih dana u školi ili sredini u kojoj živite. Predstavite neki svoj projekt s pomoću stiropora.

Za pripremu kolača upotrebljava se šuplji valjak koji se napuni toplom vodom ako se priprema dizano tijesto ili hladnom za prhko tijesto za kekse. Trebate napuniti valjak vodom. Koliko vode stane u valjak koji je dugačak i širok Svaka je ručkica dugačka Debljina stijenke valjka iznosi
Za izračunavanje volumena tekućine potrebni su visina i polumjer. Za visinu valjka oduzmite od ukupne duljine valjka dvije ručkice ( ) i debljinu stijenke na oba kraja valjka ( ). Od promjera valjka oduzmimo debljinu stijenke ( ) i raspolovimo za polumjer baze.
U valjak stane oko vode.

Cisterna s vodom može odjedanput dopremiti oko vode. Vanjske mjere cisterne iznose: duljina oko a promjer je oko
Stane li litara vode u cisternu u obliku valjka danih dimenzija?
Svaka obitelj ima spremnika vode. Koje su minimalne dimenzije spremnika potrebne da bi sva količina dopremljene vode stala u te spremnike?
(duljina × širina × visina u
)
Pomoć:
Izračunajte površinu baze svih spremnika.
Kada bi spremnici bili u obliku kocke, kolika bi trebala biti duljina brida spremnika u centimetrima?
Za te je spremnike potreban prostor od najmanje
Znate li sličan analogon piramidi, koja vam je već poznata?
Riječ je o stošcu, geometrijskom tijelu s kojim ćemo se
upoznati
u sljedećoj jedinici.
Prije toga provjerite jeste li naučili elemente valjka i svladali računanje nepoznatih elemenata valjka.
Koje su tvrdnje točne za valjak?
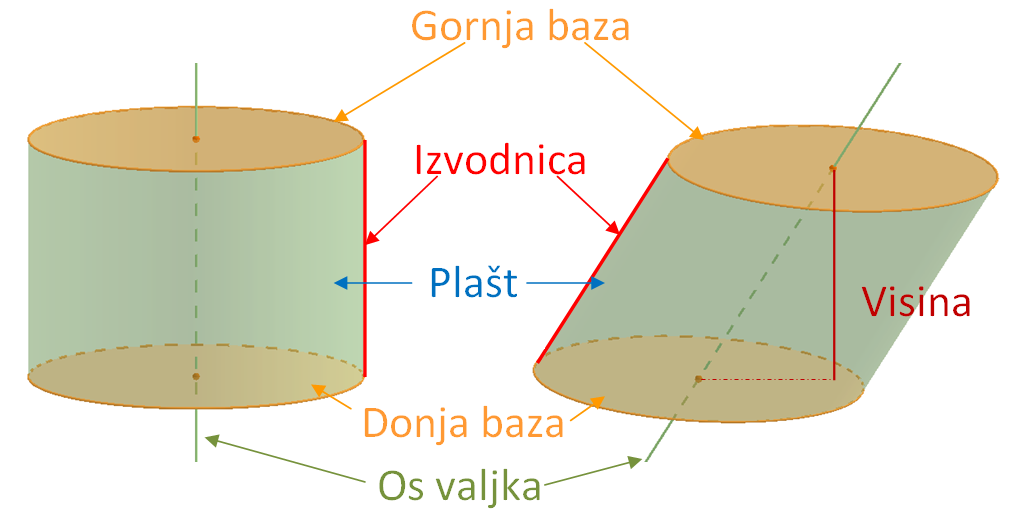
Postavite nazive elemenata valjka na crtu gdje pripadaju.
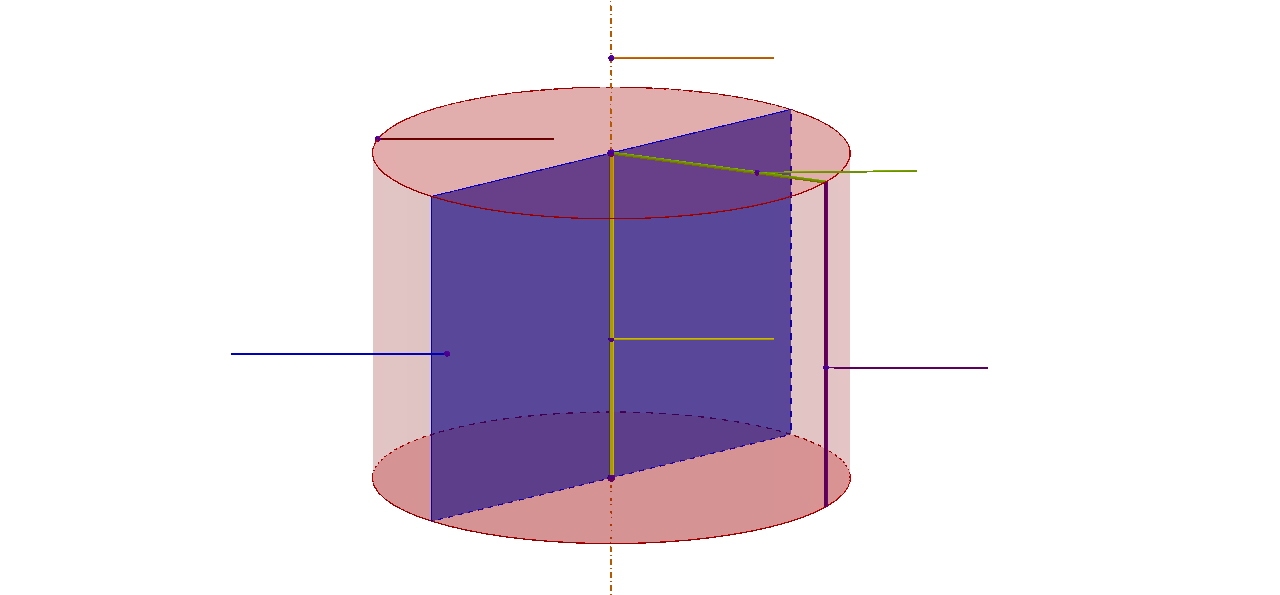
Baza
Os valjka
Polumjer baze
Visina
Izvodnica
Osni presjek
Pomoć:
