Matematika 2 - 10.3 Krnji stožac

Na početku...

Stolna lampica sa sjenilom oblika krnjeg stošca. — Izvor: Pixabay.com

Ivana je dobila noćnu svjetiljku. Visina sjenila za svjetiljku jednaka je promjeru donjeg kruga i iznosi $16 cm .$ Promjer donjeg kruga je dvostruko veći od promjera gornjeg kruga.

Međutim, Ivani se ne sviđa boja. Htjela bi promijeniti crveno sjenilo. Koliko materijala mora kupiti da bi obložila postojeću svjetiljku novim sjenilom?

Pomognimo Ivani izračunati površinu sjenila. Kakvog je oblika sjenilo za noćnu svjetiljku? Podsjeća na stožac, ali nedostaje vrh. Istražimo najprije novo geometrijsko tijelo, stožac kojem nedostaje vrh – krnji stožac.

Pogledajte u maloj galeriji slika gdje se može pronaći krnji stožac. Znadete li još neki primjer?

Primjeri predmeta u stvarnom životu oblika krnjeg stošca.

Pojam i elementi uspravnoga krnjeg stošca

Pogledajte sljedeću animaciju presjeka stošca ravninom usporednom s ravninom baze.

Nastajanje krnjeg stošca

Krnji stožac je geometrijsko tijelo koje nastaje presjecanjem stošca ravninom usporednom s ravninom osnovke i odbacivanjem manjeg stošca.

Uspravni krnji stožac je dio ravnine omeđen dvjema

. Bazu čine dva

, a plašt je

. Udaljenost između dviju baza je

krnjeg stošca.

dio kružnog vijenca

kruga

bazama

visina

plaštom

null

Koji geometrijski lik dobijemo kao presjek krnjeg stošca s ravninom koja prolazi promjerima baza okomito na ravninu osnovke?

krug

pravokutnik

trapez

konveksni četverokut

trokut

null

Ako je krnji stožac uspravan, tada govorimo o karakterističnom presjeku krnjeg stošca koji je okomit na baze.

Koji je geometrijski lik karakterističan presjek krnjeg stošca?

paralelogram

jednakokračni trapez

jednakokračni trokut

pravilni mnogokut

null

Zadatak 1.

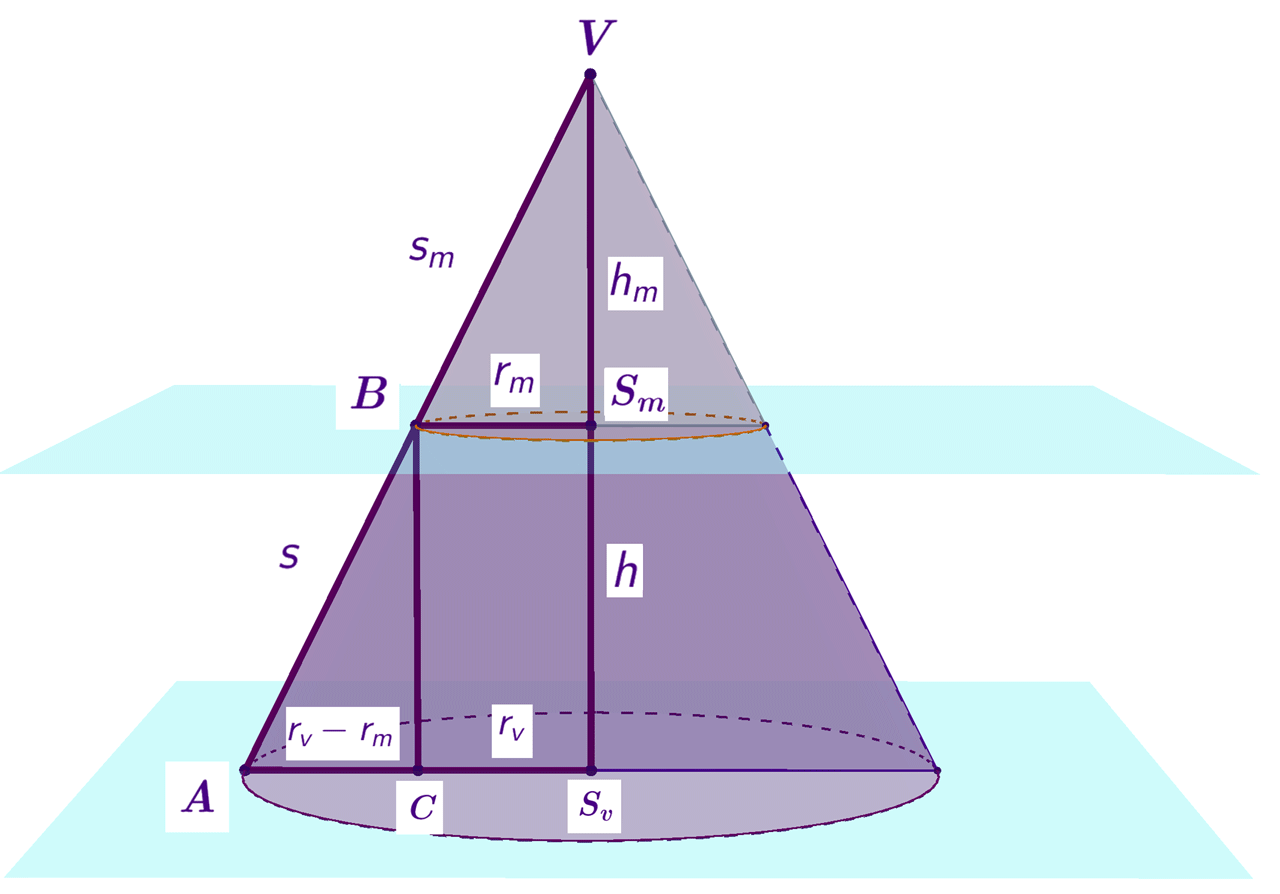
Uočite na slici trokute: $△ A S_{v} V$ i $△ B S_{m} V .$

Razmislite i odgovorite na sljedeća pitanja.

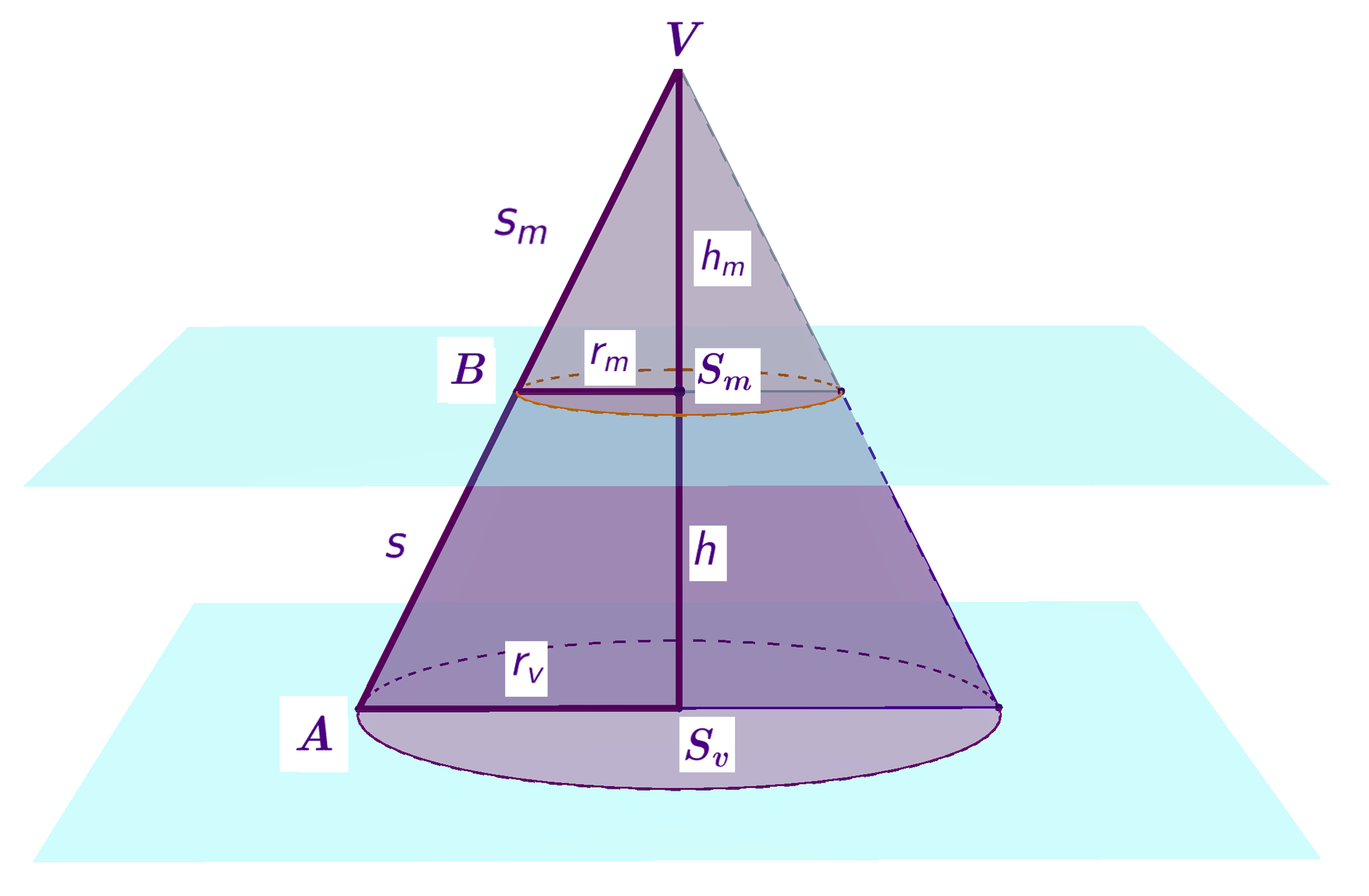
Dopunjena krnja piramida s istaknutim sličnim trokutima

Mreža uspravnog krnjeg stošca

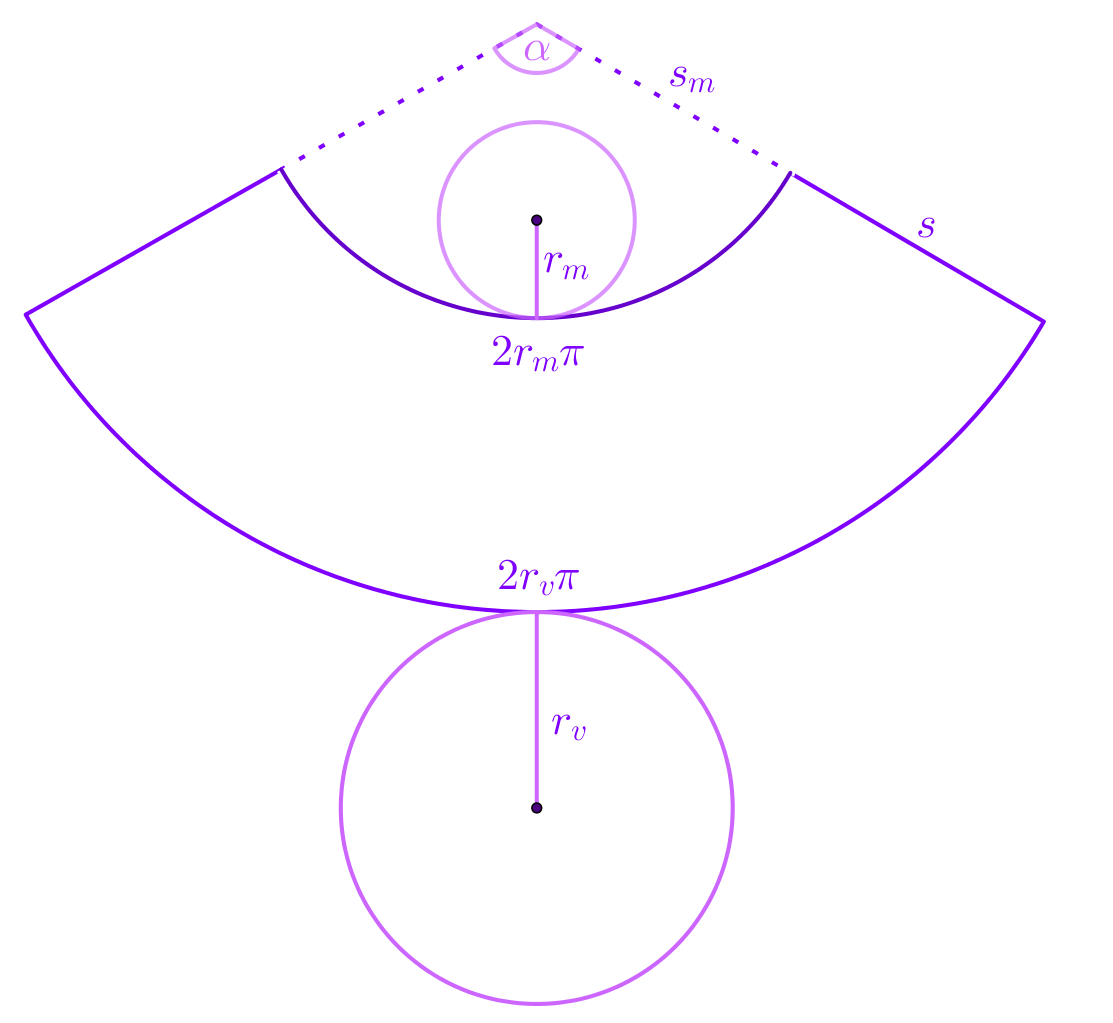
Mreža uspravnog krnjeg stošca sastoji se od

dijela:

kruga i dijela

.
Krug polumjera

$r_{v}$ je

s površinom

.

Krug polumjera

$r_{m}$ je

s površinom

.
Površina dijela kružnog vijenca dobije se

površine kružnog isječka manjeg stošca

od površine kružnog isječka većeg stošca

donja baza

dva

$r_{m} π s_{m}$

tri

$B_{v} = {r_{v}}^{2} π$

$B_{m} = {r_{m}}^{2} π$

kružnog vijenca

$r_{v} π (s + s_{m})$

gornja baza

oduzimanjem

null

Oplošje krnjeg stošca

Oplošje krnjeg stošca dobijemo zbrajanjem svih površina koje ga omeđuju.

$O = B_{v} + B_{m} + P$

Kutak za znatiželjne

Izvedite formulu za oplošje krnjeg stošca koristeći se oznakama s pomoću kojih smo definirali mrežu krnjeg stošca.

Uputa: Uočite na slici još jedan par sličnih trokuta: $△ A C B \sim △ B S_{m} V,$ te primijenite proporciju tako da se iz formule „riješite” veličine koja ne pripada krnjem stošcu, $s_{m} .$

$O = B_{v} + B_{m} + P = {r_{v}}^{2} π + {r_{m}}^{2} π + r_{v} π (s + s_{m}) - r_{m} π s_{m}$

$O = {r_{v}}^{2} π + {r_{m}}^{2} π + r_{v} π s + π s_{m} (r_{v} - r_{m})$

Uvrstimo $s_{m}$ iz proporcije $s_{m} : s = r_{m} : (r_{v} - r_{m}) .$

$O = {r_{v}}^{2} π + {r_{m}}^{2} π + s π (r_{v} + r_{m})$

Oplošje uspravnoga krnjeg stošca s polumjerima baza $r_{v} i r_{m}$ te izvodnicom $s$ dano je formulom: $O = {r_{v}}^{2} π + {r_{m}}^{2} π + s π (r_{v} + r_{m}) .$

Zadatak 2.

Izračunajte oplošje uspravnoga krnjeg stošca kojemu su polumjeri baza $6 cm i 2 cm .$

Visina je za $1 cm$ manja od promjera gornje baze.

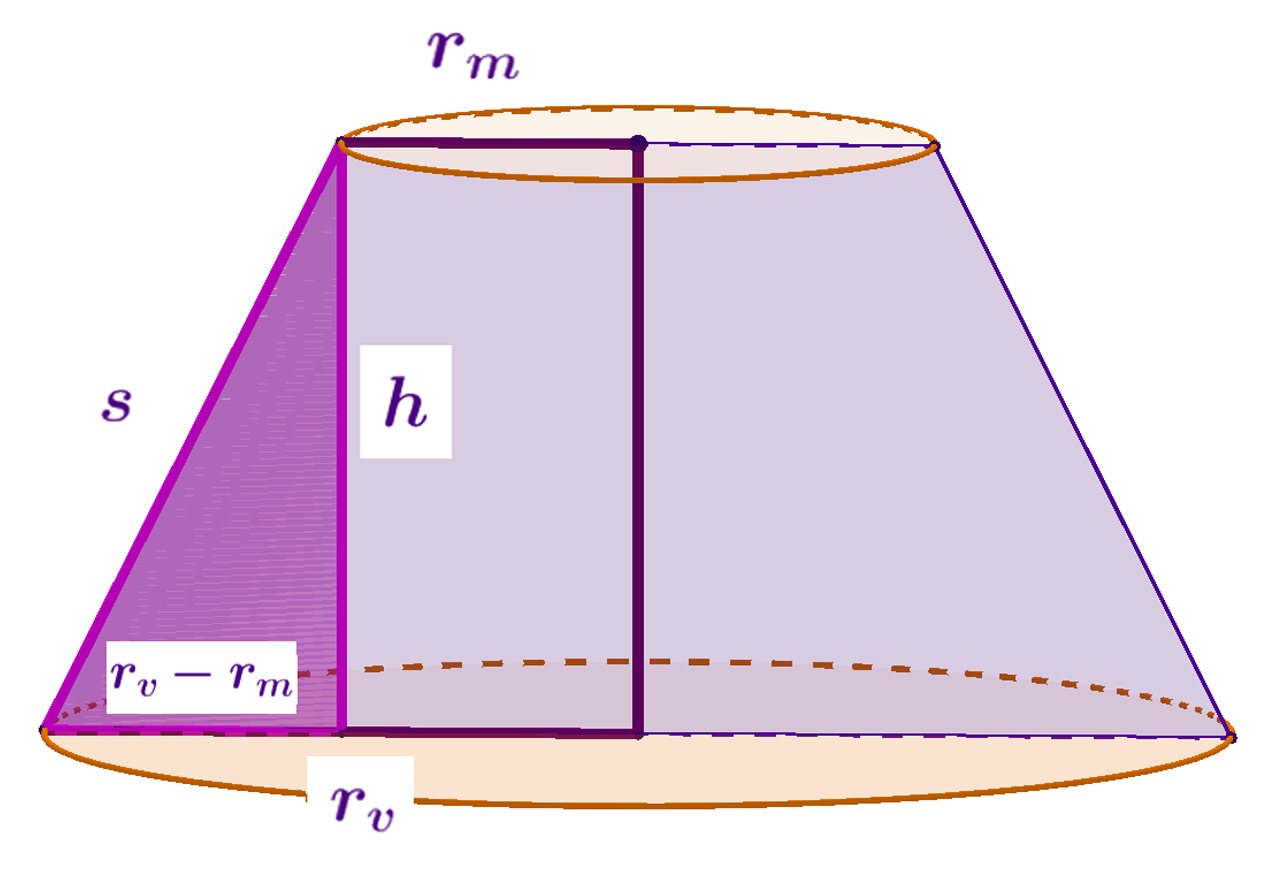
Skica krnjeg stošca s istaknutim trokutom za računanje izvodnice.

$h = 3 \Rightarrow s = 5$

$O = 80 π {cm}^{2}$

Obujam krnjeg stošca

Obujam krnjeg stošca možemo dobiti oduzimanjem obujma manjeg stošca (dopunjka) od obujma cijelog stošca.

$V = V_{v} - V_{m} = \frac{1}{3} B_{v} \cdot (h + h_{m}) - \frac{1}{3} B_{m} \cdot h_{m}$

Iz proporcije koju dobijemo iz sličnih trokuta moramo prikazati $h_{m}$ s pomoću elemenata krnjeg stošca.

Međutim, formulu lakše i brže možemo dokazati koristeći se Cavalierijevim principom ako znamo obujam krnje piramide kojoj su jednake površine baza te visina jednaka kao i kod krnjeg stošca. Na slici vidite primjer s jednakim površinama baza i jednakim visinama.

Obujam krnje piramide je $V = \frac{1}{3} h (B_{v} + \sqrt{B_{v} B_{m}} + B_{m}) .$

Uvrstimo formule za površinu kruga $(B_{v} = {r_{v}}^{2} π i B_{m} = {r_{m}}^{2} π)$ i dobijemo formulu za obujam krnjeg stošca.

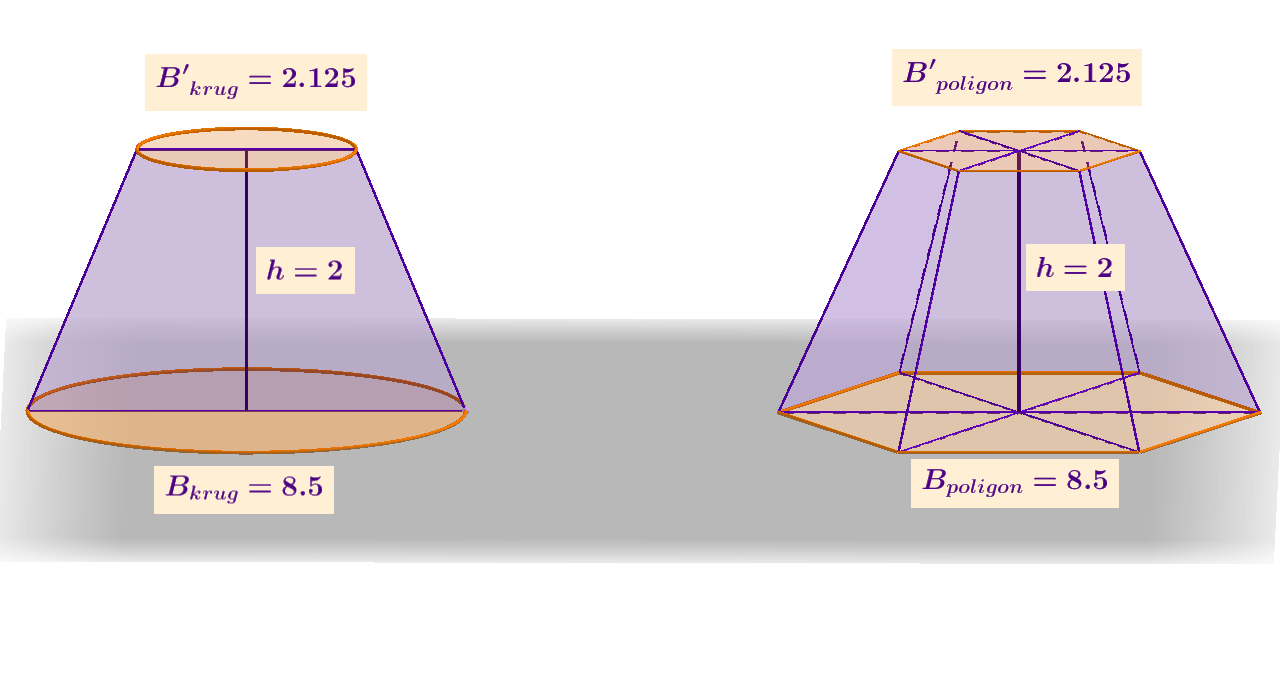
Usporedba krnje piramide i krnjeg stošca, Cavalieriv princip, jednaki volumeni.

Obujam krnjeg stošca s polumjerima baza $r_{v} i r_{m}$ te visinom $h$ dan je formulom $V = \frac{h π}{3} ({r_{v}}^{2} + r_{v} r_{m} + {r_{m}}^{2}) .$

Zadatak 3.

Odredite obujam krnjeg stošca (i krnje piramide) sa zadanim elementima kao na gornjoj slici. Izračunajte polumjere donje i gornje baze te oplošje uspravnoga krnjeg stošca. Imamo li dovoljno podataka za izračun oplošja pravilne šesterostrane krnje piramide? Izračunajte.

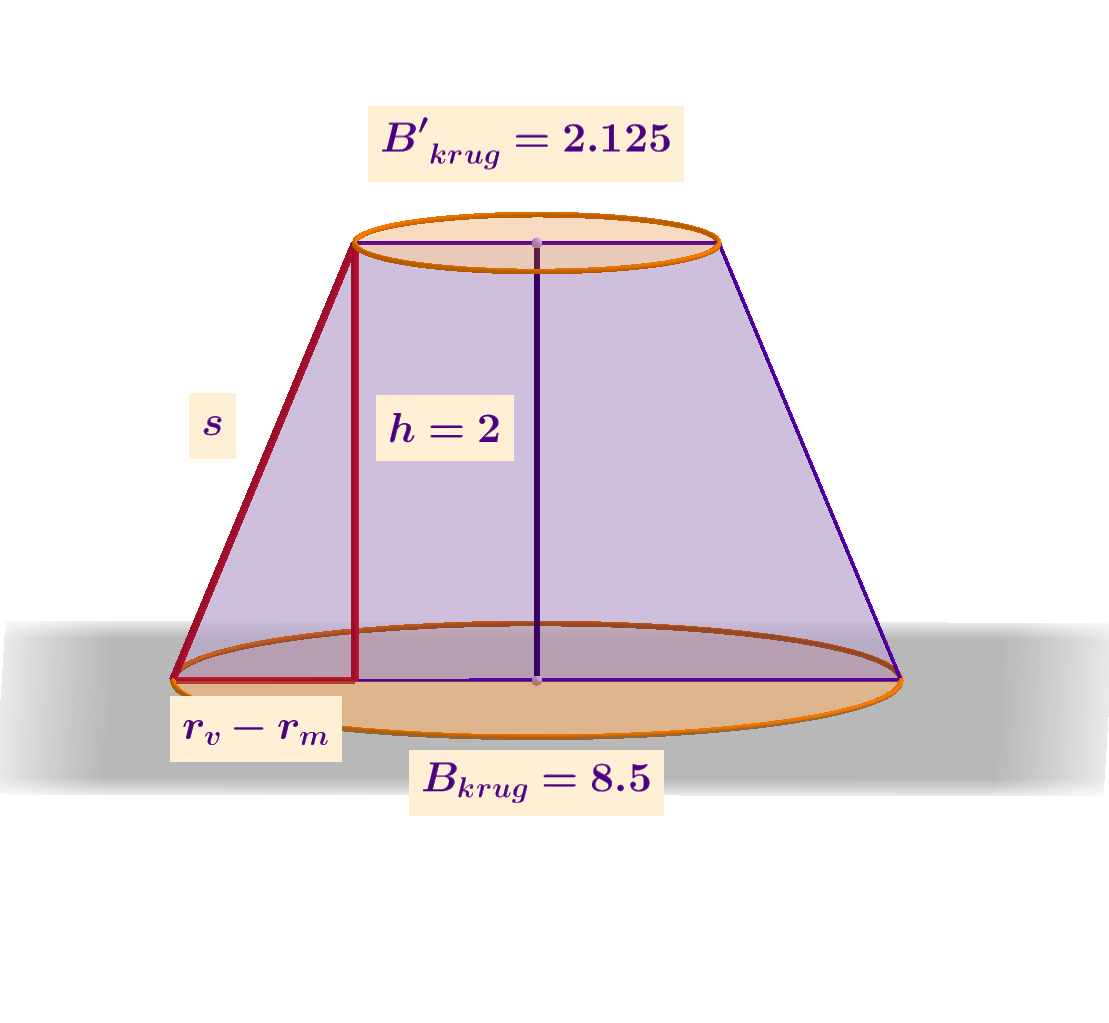
Skica krnjeg stošca s istaknutim trokutom sa izvodnicom.

$V = \frac{1}{3} h (B_{v} + \sqrt{B_{v} B_{m}} + B_{m}) = \frac{2}{3} (8.5 + \sqrt{18.0625} + 2.125) = 9.9$

$r_{v} = 1.6, r_{m} = 0.8$

Na slici je istaknut trokut iz kojeg možemo izračunati izvodnicu.

$s = 2.15$

Iskoristimo zadane površine baza za oplošje: $O = {r_{v}}^{2} π + {r_{m}}^{2} π + s π (r_{v} + r_{m}) = 8.5 + 2.125 + 2.15 π \cdot 2.4 = 26.8 .$

Krnjoj piramidi možemo izračunati duljinu osnovnog brida donje i gornje baze s pomoću formule: $B = 6 \cdot \frac{a^{2} \sqrt{3}}{4} .$ Izračunajmo stranicu donje baze te uočimo omjere sličnih trokuta. Prisjetimo se čemu je jednak omjer površina baza. Iskoristimo to i izračunajmo preostale elemente krnje piramide.

$a_{v} = 1.81$

$\begin{array}{l} \frac{B_{v}}{B_{m}} = {(\frac{a_{v}}{a_{m}})}^{2} \Rightarrow {a_{m}}^{2} = 0.82 \Rightarrow a_{m} = 0.905 \end{array}$

$O = B_{v} + B_{m} + 6 \cdot \frac{a_{v} + a_{m}}{2} \cdot h = 26.9$

Kutak za znatiželjne

Dokažite formulu za obujam krnjeg stošca oduzimanjem manjeg od većeg obujma stošca. Nastavite dokaz:

$\begin{array}{l} V = V_{v} - V_{m} = \frac{1}{3} B_{v} \cdot (h + h_{m}) - \frac{1}{3} B_{m} \cdot h_{m} \end{array} .$

Uputa: primijenite proporciju sličnih trokuta da biste se u izrazu riješili veličine $h_{m} .$

Puni stožac s pripadajućim oznakama sličnih trokuta.

$\begin{array}{l} △ A S_{v} V \sim △ B S_{m} V \Rightarrow r_{v} : r_{m} = (h + h_{m}) : h_{m} \end{array}$

$\begin{array}{l} h_{m} = \frac{h \cdot r_{m}}{r_{v} - r_{m}} \Rightarrow h + h_{m} = \frac{h \cdot r_{v}}{r_{v} - r_{m}} \end{array}$

$\begin{array}{l} V = V_{v} - V_{m} = \frac{1}{3} {r_{v}}^{2} π \cdot \frac{h \cdot r_{v}}{r_{v} - r_{m}} - \frac{1}{3} {r_{m}}^{2} π \cdot \frac{h \cdot r_{m}}{r_{v} - r_{m}} = \frac{h π}{3} \cdot \frac{{r_{v}}^{3} - {r_{m}}^{3}}{r_{v} - r_{m}} \end{array}$

Uvršavanjem formule za razliku kubova te kraćenjem dobivamo traženu formulu.

Računajmo s krnjim stošcem

Kolekcija zadataka 1

Zadatak 4.

Izračunajte oplošje i obujam uspravnoga krnjeg stošca ako mu je visina $4 cm,$ izvodnica $5 cm$ i površina plašta $85 π {cm}^{2} .$

Iz sustava jednadžbi za površinu plašta i Pitagorina poučka dobijemo polumjere.

$\begin{array}{l} \begin{array}{l} P = (r_{v} + r_{m}) s π \\ {(r_{v} - r_{m})}^{2} = s^{2} - h^{2} \end{array}\} r_{v} = 10 cm, r_{m} = 7 cm \end{array}$

$O = 234 π {cm}^{2}, V = 292 π {cm}^{3}$

Zadatak 5.

Izračunajte obujam uspravnoga krnjeg stošca u kojem je $r_{v} = 2 r_{m}, P = B_{v} + B_{m},$ a površina osnog presjeka $36 m^{2} .$

$V = 84 π {cm}^{3}$

Zatvori

U sljedećoj su interakciji prikazani uspravni krnji stožac i njegov dopunjak. Pomicanjem triju crvenih točaka možete mijenjati polumjer donje baze, visinu krnjeg stošca te visinu cijelog stošca.

Poigrajte se i istražite kako tražene veličine ovise o zadanim elementima.

Kutak za znatiželjne

Izračunajte obujam kosoga krnjeg stošca s polumjerima $10 cm i 3 cm .$ Najveća izvodnica iznosi $15 cm,$ a najmanja $13 cm .$

Uputa: Iz trapeza se dobije trokut s poznatim stranicama. Visinu možete dobiti metodom površina. Izjednačite Heronovu formulu s formulom za površinu s pomoću stranice i pripadajuće visine.

$h = 12 cm, V = 556 π {cm}^{3}$

10.3 Krnji stožac

Na početku...

Pojam i elementi uspravnoga krnjeg stošca

Zadatak 1.

Mreža uspravnog krnjeg stošca

Oplošje krnjeg stošca

Kutak za znatiželjne

Zadatak 2.

Obujam krnjeg stošca

Zadatak 3.

Kutak za znatiželjne

Računajmo s krnjim stošcem

Kolekcija zadataka 1

Zadatak 4.

Zadatak 5.

Kutak za znatiželjne

...i na kraju

10.4 Kugla