7.5 Logaritamske nejednadžbe

Logaritamska nejednadžba

Primjer 1.

Neki primjeri logaritamskih nejednadžbi su:​ ${\log }_2\left(3x+4\right)\ge 0,$ $\log x^2+{\log }^{2}x\le 3,$ ${\log }_{x-1}3>1.$

Dovucite zadane elemente na pravo mjesto.

${10}^{2x-1}>1$

${\log }_{2}x=5$

$3^{{\log }_{2}16}<2^x$

${\log }_{x}10\le 2$

${\log }_2\left(x+1\right)>3$

$x^2<{\log }_{2}e$ 

$x^3\le 4$

 Logaritamske nejednadžbe

 Eksponencijalne nejednadžbe

 Ostalo

null

null

Primjer 2.

Pogledajmo kako bismo riješili uvodni primjer da imamo jednadžbu: $\log 48-0.3\log \left(t+1\right)=\log 28.$

Nepoznanicu ostavimo na lijevoj strani, pomnožimo s $-1$ i dobivamo

$0.3\log \left(t+1\right)=\log 48-\log 28.$

Razliku logaritama s desne strane svedemo na logaritam kvocijenta

$0.3\log \left(t+1\right)=\log \frac{48}{28}$ .

Izračunajmo sada logaritam i podijelimo ga s $0.3.$ Dobit ćemo

$\log \left(t+1\right)=0.780277$ .

Kako je logaritam po bazi $10,$ da bismo se oslobodili logaritma djelujemo s eksponencijalnom funkcijom s bazom $10$

$t+1=6.0294.$

Odnosno $t=5.0294.$

Odredili smo da je vrijeme za koje će Marta zaboraviti gradivo točno do ocjene dobar nešto više od $5$ mjeseci. Kako se test provodio u siječnju, Marta bi bez ponavljanja gradiva mogla na završnom testu dobiti ocjenu dobar.

Ipak, odlučila je da će prije završnog testa ponoviti sve sadržaje iz matematike.

Odgovor na naše pitanje dobili smo bez rješavanja nejednadžbe. Jesmo li dobro razmišljali? Koja je razlika u tome rješavamo li nejednadžbu u odnosu na jednadžbu? Možemo li uvijek umjesto znaka nejednakosti staviti znak jednakosti?

Zadatak 1.

Spojite nejednadžbe s njihovim rješenjima.

$2x>-4$	x<2x>-2
$-2x>-4$	x<2x>-2

null

null

Kod linearnih nejednadžbi naučili smo da se smjer znaka nejednakosti mijenja kad množimo ili dijelimo s negativnim brojem. Zašto?

Pogledamo li funkciju $f\left(x\right)=2x,$ uočavamo da je ona monotono rastuća: što je $x$ veći, to je i $y$ veći.

Pogledamo li funkciju $f\left(x\right)=-2x,$ uočavamo da je ona monotono padajuća: što je $x$ veći, to je $y$ manji. ​

Grafičko rješavanje logaritamskih nejednadžbi

Prisjetimo se monotonosti logaritamske funkcije. Na idućem grafičkom prikazu možete pomicati točke i pratiti njihove koordinate.

Zatim promijenite vrijednost baze i ponovno pomičite točke.

Što se događa s vrijednostima koordinata točaka?

Zadatak 2.

Kad je baza logaritamske funkcije $f\left(x\right)={\log }_{a}x$ veća od $1,$ $a>\mathrm{1,}$ funkcija je

 

.
Što je $x$ veći, to je vrijednost funkcije $y$

 

.
Kad je baza logaritamske funkcije $f\left(x\right)={\log }_{a}x$ između $0$ i $1,$ $0<a<1,$ funkcija je

 

.
Što je $x$ veći, to je vrijednost funkcije $y$

 

.

rastuća

manja

padajuća

veća

null

null

Primjer 3.

Grafički riješimo logaritamsku nejednadžbu ${\log }_{2}x>1.$

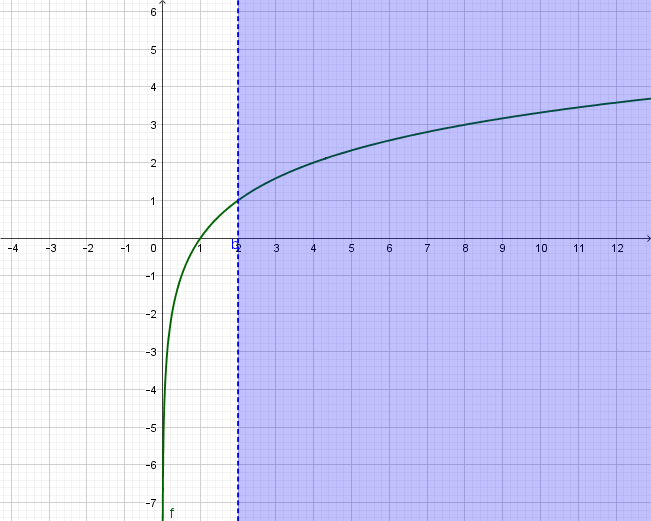
Graf logaritamske funkcije s bazom $2$ istaknut je zelenom bojom. Vrijednost logaritma po bazi $2$ jednaka je $1$ za $x=2.$

Možemo zaključiti da je vrijednost funkcije ​ $f\left(x\right)={\log }_{2}x$ veća od $1$ za sve $x>2.$

Primjer 4.

Grafički riješimo logaritamsku nejednadžbu ${\log }_{\frac{1}{2}}x>1.$  

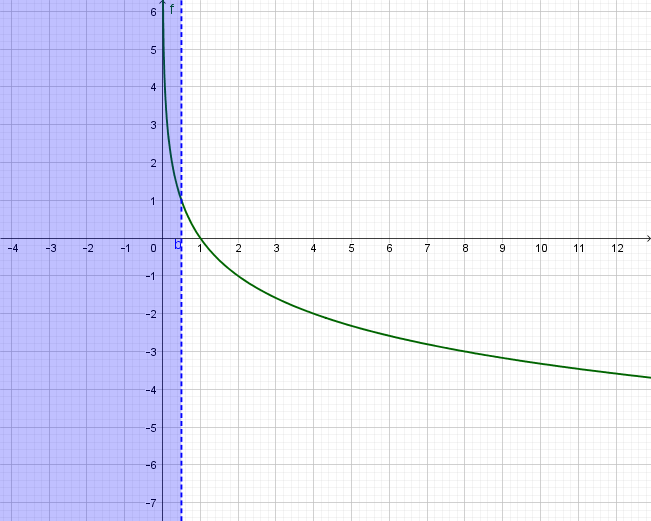
Graf logaritamske funkcije s bazom $\frac{1}{2}$ istaknut je zelenom bojom. Vrijednost logaritma po bazi $\frac{1}{2}$ jednaka je $1$ za $x=\frac{1}{2}.$ Možemo zaključiti da je vrijednost funkcije $f\left(x\right)={\log }_{\frac{1}{2}}x$ veća od $1$ za sve $x<\frac{1}{2}.$ No pogledamo li još jedanput grafički prikaz, uočit ćemo da graf funkcije za negativne vrijednosti od $x$ ne postoji.

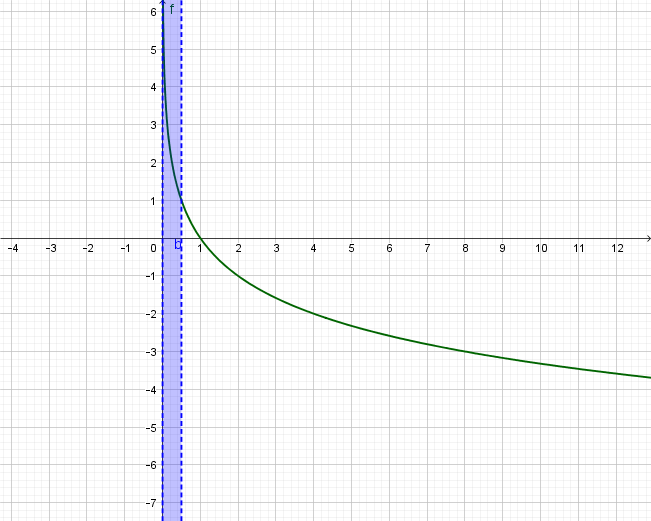
Stoga je rješenje naše nejednadžbe $x\in ⟨0,\frac{1}{2}⟩.$

Zadatak 3.

Baza logaritamske funkcije uvijek je

 

od $0$ i

 

od $1,$ a argument

 

od $1.$

veći

različita

veća

null

null

Kod rješavanja logaritamske nejednadžbe ${\log }_{2}x>1$ dobili smo rješenje $x>2.$

Kod rješavanja logaritamske nejednadžbe ${\log }_{\frac{1}{2}}x>1$ dobili smo rješenje $x<\frac{1}{2},$ uz uvjet $x>0.$

Rješavanje logaritamskih nejednadžbi s pomoću svojstava logaritamske funkcije

Logaritamske nejednadžbe možemo rješavati poznavajući graf i svojstva logaritamske funkcije.

1. Ako je baza $a>1,$ onda vrijedi: ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)\Rightarrow f\left(x\right)>g\left(x\right).$
2. Ako za bazu vrijedi $0<a<1,$ onda: ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)\Rightarrow f\left(x\right)<g\left(x\right).$

Pritom moramo uvažiti da je logaritamska funkcija definirana samo za $f\left(x\right)>0$ i $g\left(x\right)>0.$

Primjer 5.

Riješimo nejednadžbu ​ ${\log }_2\left(3x-6\right)\le {\log }_{2}3.$

Kako je baza veća od $1,$ nejednadžba je ekvivalentna nejednadžbi $3x-6\le 3,$ uz uvjet $3x-6>0.$

Rješavajući nejednadžbu dobijemo $x\le 3,$ uz uvjet $x>2.$

Presjek tih dviju nejednadžbi daje interval $x\in \left.⟨2,3\right].$

Primjer 6.

Riješimo nejednadžbu​ ${\log }_{\frac{1}{2}}\left(x+5\right)<{\log }_{\frac{1}{2}}\left(2x-1\right).$

Kako je baza manja od $1,$ nejednadžba je ekvivalentna nejednadžbi​ $x+5>2x-1,$ uz uvjet $x+5>0$ i $2x-1>0.$

Rješenje nejednadžbe je $x<6,$ a uvjeta $x>-5$ i $x>\frac{1}{2}.$

Presjek ovih triju nejednadžbi je interval $⟨\frac{1}{2},6⟩.$

Zadatak 4.

Riješimo logaritamsku nejednadžbu ${\log }_{0.5}x+{\log }_{0.5}\left(x-3\right)\ge -2.$

Rješenje je detaljno objašnjeno u videu koji slijedi.

Zadatak 5.

Spojite logaritamske nejednadžbe s intervalima rješenja.

$\log \left(x-2\right)>\log \left(x+1\right)$	$⟨1,+\infty ⟩$
${\log }_{\frac{1}{2}}\left(4x-3\right)<0$	$\left[-1,+\infty \right.⟩$  ​
$\log \left(x+1\right)\le \log \left(2x\right)$	$\varnothing$
${\log }_2\left(3x+4\right)\ge 0$	$\left[1,+\infty \right.⟩$

null

null

Rješavanje logaritamskih nejednadžbi s pomoću inverzne funkcije

Funkcija $g$ inverzna je funkciji $f$ ako vrijedi:

• $g\left(f\left(x\right)\right)=x$ za svaki $x\in D_f$
• $f\left(g\left(x\right)\right)=x$ za svaki $x\in D_g$ $.$
  

Oznaka za inverznu funkciju od funkcije $f$ je ​ $f^{-1}.$

Zadatak 6.

 Spojite međusobno inverzne funkcije.

${0.5}^x$	${\log }_{0.5}x$
${\log }_{3}x$	$3^x$
$\log x$	${\log }_{\frac{1}{3}}x$
${\left(\frac{1}{3}\right)}^x$	${10}^x$  ​

null

null

Logaritamske nejednadžbe možemo rješavati i djelujući inverznom funkcijom. Inverzna funkcija od logaritamske je eksponencijalna funkcija s istom bazom.

Stoga vrijedi: ${\log }_a{a}^x=x$  i $a^{{\log }_{a}y}=y.$

Pritom također moramo razmišljati o uvjetima za argument logaritma i bazu.

Primjer 7.

Riješimo nejednadžbu ​ ${\log }_{\frac{1}{3}}\left(1-x\right)\le 1.$

Inverzna funkcija od funkcije $f\left(x\right)={\log }_{\frac{1}{3}}x$  je $f^{-1}\left(x\right)={\left(\frac{1}{3}\right)}^x.$

Kako je baza manja od $1,$ funkcija je padajuća - smjer nejednakosti se mijenja.

${\left(\frac{1}{3}\right)}^{{\log }_{\frac{1}{3}}\left(1-x\right)}\ge {\left(\frac{1}{3}\right)}^1$

$1-x\ge \frac{1}{3}$

$x\le \frac{2}{3}$

Kako je uvjet za argument logaritma $1-x>0,$ tj. $x<1,$ presjek uvjeta i rješenja je ​ $x\in ⟨-\infty ,\frac{2}{3}⟩.$

Zadatak 7.

Riješite nejednadžbu ${\log }_{0.5}\left(x^2-4x+3\right)\ge -3.$

Rješavanje logaritamskih nejednadžbi metodom supstitucije

Neke logaritamske nejednadžbe možemo pojednostavniti upotrebom supstitucije te svesti na već poznate tipove nejednadžbi.

Primjer 8.

Riješimo nejednadžbu $\log x^2+{\log }^{2}x\le 3.$

Uočite razliku između ovih dvaju logaritama. U prvome je argument na kvadrat $\log x^2=2\log x,$ a u drugome je vrijednost logaritma na kvadrat ${\log }^{2}x={\left(\log x\right)}^2.$​

Imamo $2\log x+{\left(\log x\right)}^2\le 3.$

Uvrstimo li umjesto $\log x$ varijablu $t,$ dobit ćemo kvadratnu nejednadžbu $2t+t^2\le 3.$ Rješenje te kvadratne nejednadžbe je interval $\left[-3,1\right].$

Dakle $\log x\in \left[-3,1\right].$

Djelujemo li s inverzom funkcijom, dobit ćemo da je $x\in \left[{10}^{-3},{10}^1\right].$

Uvjet za argument je $x>0.$ Rješenje naše nejednadžbe je interval $x\in \left[0.001,10\right].$

Zadatak 8.

Riješite nejednadžbu ​ ${{\log }_3}^{2}x-3{\log }_{3}x\le -2$ .

Kutak za znatiželjne

Odredite sve cijele brojeve $x$ za koje vrijedi ${\log }_4\left(x+12\right)·{\log }_{x}2\ge 1.$