

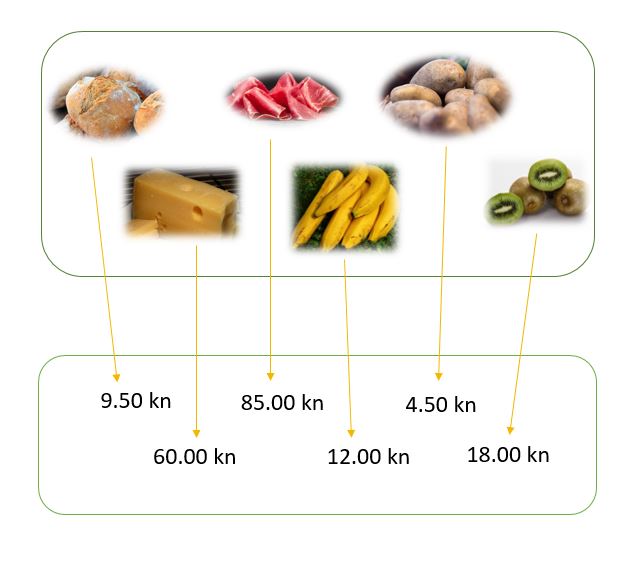
Krenuli ste u dućan. Na popisu za kupovinu imate kruh, kivi, banane, krumpir, šunku i sir. Međutim, zaboravili ste od kuće ponijeti novac. S vama je prijatelj koji će vam rado pomoći, ali ne zna ima li dovoljno novca za sve. Stoga najprije morate pogledati cijene da biste znali možete li sve kupiti. Svakom proizvodu ćete pridružiti iznos u kunama kao na slici.
U prethodnoj smo jedinici 6.1 logaritamsku funkciju definirali kao inverz eksponencijalne funkcije. Funkcija je pridruživanje kojim se svakom elementu iz domene pridružuje točno jedan element iz kodomene. Što znači "inverz"? Provjerimo najprije jesmo li razumjeli istaknute riječi u definiciji funkcije.
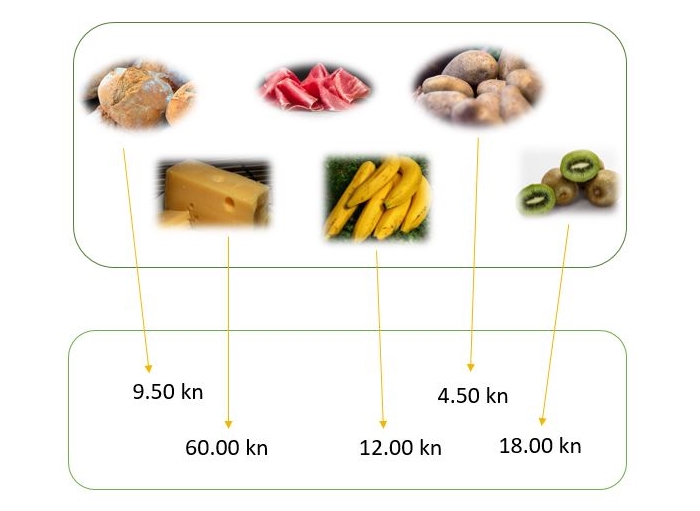
Zaključili ste da za šunku nemate novca. Na slici je prikazano novo pridruživanje, gdje je jedan element ostao bez svoje vrijednosti (na polici, umjesto u košari).
Je li takvo preslikavanje funkcija?
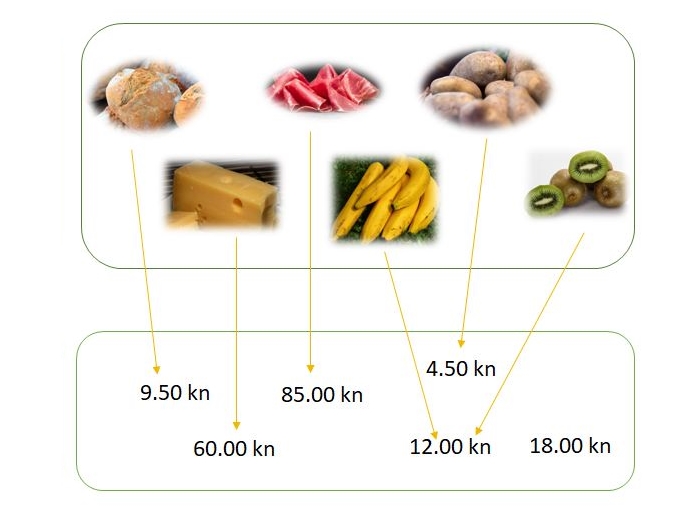
Primijetili ste da je kivi na popustu i sada mu je cijena kao i bananama.
Je li tako definirano preslikavanje funkcija?
Vrijedi li za ovako definirano pridruživanje sljedeće svojstvo za različite elemente domene funkcije :
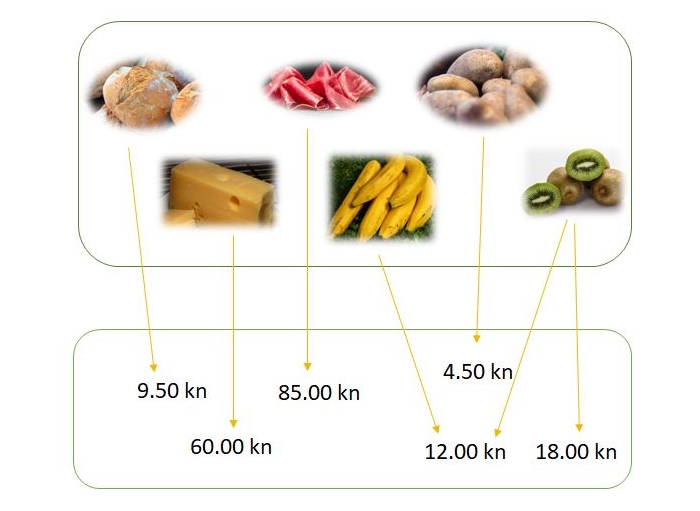
Na jednome mjestu u dućanu istaknuta je cijena kivija s popustom, a na drugom cijena bez popusta. Kako niste sigurni koja je prava cijena, pridružili ste obje cijene ( i ) istom elementu (kiviju).
Je li to preslikavanje funkcija?
Zaključimo. Funkciju zadajemo domenom
kodomenom
i pridruživanjem
kojim svakom elementu iz domene (u domeni ne smije ostati elemenata kojima nije pridružena niti jedna vrijednost iz kodomene) pridružujemo točno jedan element iz kodomene (ne možemo pridružiti jednom elementu iz domene više od jednog elementa iz kodomene). U kodomeni može biti "neiskorištenih" elemenata.
Funkcija je injekcija ako različitim elementima iz domene pridružujemo različite elemente iz kodomene.
Je li neki graf doista graf funkcije i je li funkcija injekcija, ispitujemo vertikalnim i horizontalnim testom.
Povežite što ispitujemo kojim testom.
|
Horizontalni test
|
Funkcija je injekcija |
|
Vertikalni test
|
Krivulja je graf funkcije |
Funkcija je injekcija ako za svaka dva različita elementa iz domene funkcije vrijedi:
Može se pokazati da je ovo ekvivalentno sljedećoj tvrdnji:
Vratimo se u dućan. Stavili ste na papir sve cijene. Napravimo sada obrnuto pridruživanje. Cijenama pridružimo proizvode koje možemo kupiti za taj iznos.
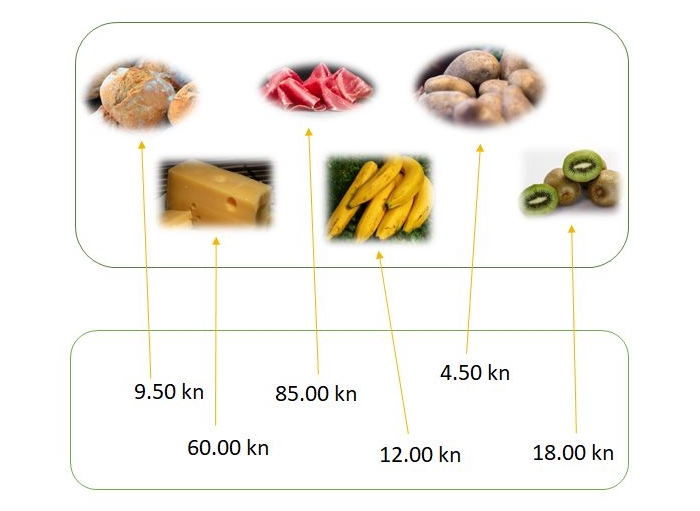
Je li preslikavanje sa slike funkcija?
Za preslikavanje koje svakom elementu iz kodomene pridružuje točno jedan element iz domene zadane funkcije kažemo da je
inverzno (obrnuto) zadanom preslikavanju.
Je li "obrnuto" preslikavanje uvijek funkcija (preslikavanje iz kodomene u domenu)?
Samo ako su zadovoljeni uvjeti da bude funkcija. Svaki element (slika) iz drugog skupa mora imati svoj "original" u prvom skupu. Dva različita elementa iz drugog skupa ne mogu imati isti "original".
Zaključak: funkcija mora biti injekcija da bi imala inverz.
Razmislite i odgovorite.
Koja slika prikazuje pridruživanje za koje se može definirati inverzna funkcija?
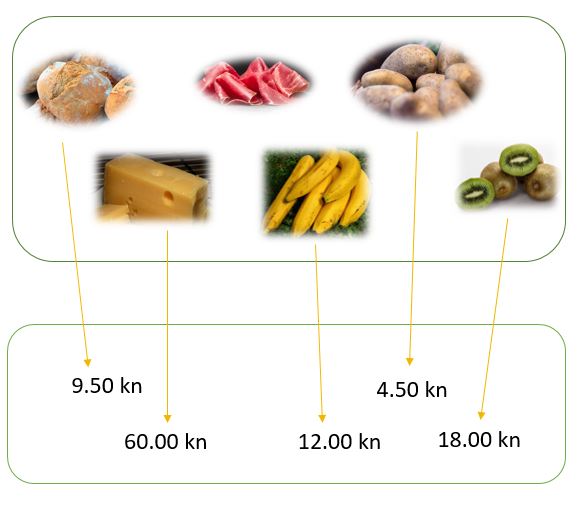
Ako je funkcija
injekcija, gdje je skup
domena, a skup
slika funkcije, tada je funkcija
za koju vrijedi da je
inverzna funkcija funkcije
Ako je funkcija injekcija, tada za proizvoljni broj postoji točno jedan takav da je Znači postoji neko "obrnuto" preslikavanje koje će broju pridružiti broj tj.
Ako u definiciji inverzne funkcije umjesto
stavimo
imamo:
Funkcije za koje vrijedi ovo svojstvo (da se međusobno poništavaju) čine par međusobno inverznih funkcija.
i
nazivamo kompozicija ili slaganje funkcija.
U kompoziciji prvo računamo unutarnju, a potom vanjsku funkciju.
Pišemo (čita se: "ge komponirano sa ef" ili "ge kružić ef") i
Primjer 1.
Za funkcije odredimo njihovu kompoziciju.
Vrijedi li za kompoziciju funkcija svojstvo komutativnosti, tj.
Odredite kompoziciju kvadratne funkcije i funkcije drugog korijena. Provjerite vrijedi li ovdje komutativnost. Za koje su realne brojeve kompozicije funkcija definirane?
Kvadratna funkcija je
Funkcija drugog korijena je
za sve realne brojeve
Možemo zaključiti da ove dvije kompozicije funkcija nisu jednake, jer su im domene različite.
Neka je
eksponencijalna funkcija s domenom
i slikom funkcije
Pridružimo odabranim elementima domene pripadajuće vrijednosti funkcije.
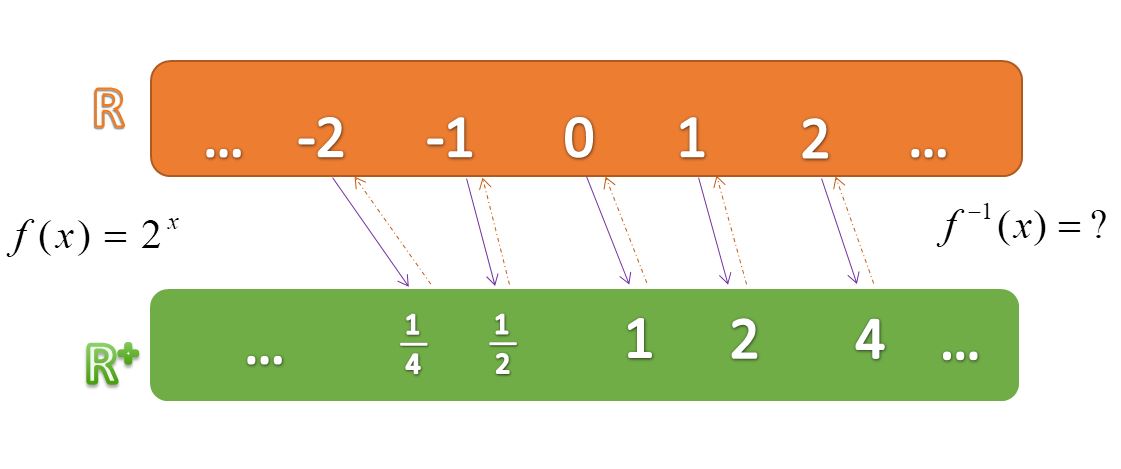
Je li eksponencijalna funkcija injekcija?
U prošloj ste jedinici definirali logaritam
kao eksponent kojim se mora potencirati baza
da bi se dobila vrijednost
Funkcija koja je time definirana pridružuje:
To možemo i ovako zapisati:
S pomoću tog zapisa definirajmo funkciju inverznu eksponecijalnoj funkciji.
Ako je eksponencijalna funkcija, tada je logaritamska funkcija.
Domena logaritamske funkcije je
Slika logaritamske funkcije je
Primjer 2.
Za inverzne funkcije vrijedi: za svaki i za svaki Uvrstimo eksponencijalnu i logaritamsku funkciju u lijevu stranu ovih identiteta.
za svaki
za svaki
Iz svojstva inverznih funkcija slijede identiteti korisni za računanje s logaritmima.
Eksponencijalna funkcija je za svaki element iz kodomene imala točno jedan "original" u domeni, odnosno niti jedan element iz kodomene nije ostao "neiskorišten" kod pridruživanja
Funkcija kod koje za svaki element iz kodomene
postoji barem jedan element iz domene
takav da je
jest surjekcija.
Funkcija je bijekcija ako je i surjekcija i injekcija. To je tzv. preslikavanje "
na
" (jednom elementu domene pripada točno jedan element kodomene). Da bi funkcija imala inverznu funkciju, mora biti bijekcija.
Eksponencijalna i logaritamska funkcija su bijekcije. Zašto?
Je li pridruživanje namirnica cijenama proizvoda (i obrnuto) iz našeg dućana bijekcija? U kojem slučaju jest, a kad nije?
Smjestimo logaritamsku funkciju u koordinatni sustav.
Kao i za eksponencijalnu funkciju, odredit ćemo nekoliko točaka koje pripadaju grafu logaritamske funkcije. U tome će nam pomoći pridruživanje sa slike kojom smo se već koristili. Napravimo tablicu i nacrtajmo graf s pomoću točaka.
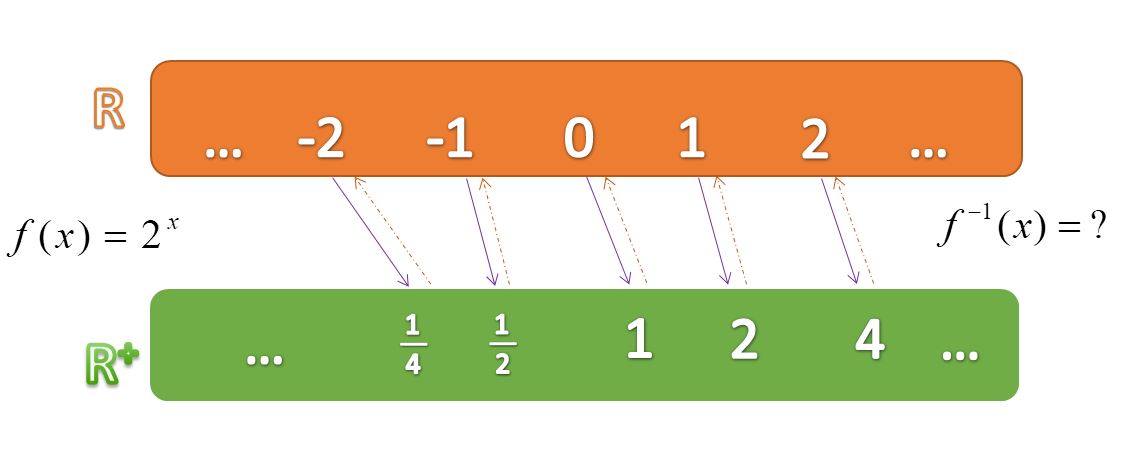
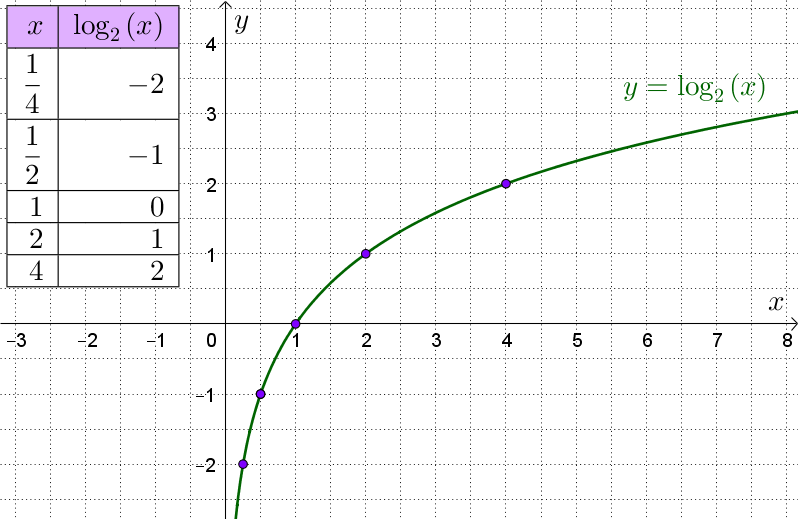
U sljedećoj interakciji, mijenjajući bazu te pomičući točku po grafu pokušajte uočiti koja svojstva ima logaritamska funkcija. Prisjetite se svojstava eksponencijalne funkcije iz prethodnog modula.
Što možemo zaključiti o logaritamskoj funkciji?
Gdje je smješten graf logaritamske funkcije
Pomoć:
U kojoj točki sve krivulje sijeku os
Točka kojom prolaze svi grafovi je logaritamske funkcije.
Kad funkcija raste, a kad pada?
|
Logaritamska funkcija je padajuća
|
|
|
Logaritamska funkcija je rastuća
|
|
Pomoć:
Kad podesite bazu
točku na krivulji pomaknite tako da apscisa bude jednaka bazi i pročitajte vrijednost ordinate.
Ponovno se vratite na interakciju te nacrtajte krivulju
Usporedite je s krivuljom
U kojem su položaju grafovi funkcija s recipročnim bazama?
Sistematizirajmo uočena svojstva na primjeru logaritamske funkcije
uz pomoć sljedeće animacije.
Koja je funkcija simetrična funkciji prirodnog logaritma
s obzirom na os
? Je li rastuća ili padajuća? Za koji argument
poprima vrijedost
Jesu li to inverzne funkcije?
To je funkcija s recipročnom bazom:
Kako je baza
funkcija je padajuća.
Da bi funkcija poprimila vrijednost, jedan argument mora biti jednak bazi, stoga vrijedi
Funkcije nisu inverzne
.
Primjer 3.
Koristeći se vezom te prethodnim svojstvima, nacrtajmo krivulje prirodnog i dekadskog logaritma.
Nacrtajmo tablicu s nekoliko točaka, ucrtajmo ih u koordinatni sustav i povucimo krivulju.
- baza prirodnog logaritma je Kako je prema definiciji logaritam eksponent kojim se mora potencirati baza, odaberimo cijele brojeve za i potencirajmo njima bazu
- baza dekadskog logaritma je Kao i za prirodni logaritam, potencirajmo odabranim točkama bazu
Dobit ćemo tablice kao ove dolje. Pokušajte sami nacrtati krivulje pa tek zatim provjerite rješenje.
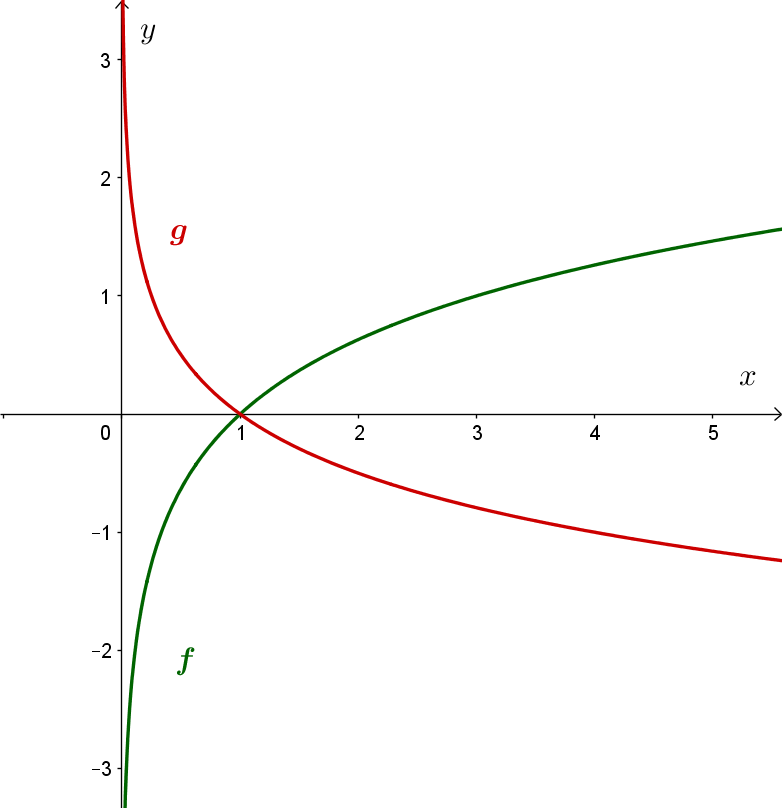
Povežite nacrtane grafove s pripadajućim jednadžbama.
Jesu li funkcije rastuće ili padajuće?
je
je
Postoji li asimptota funkcije? (Prisjetimo se, asimptota je pravac kojem se krivulja približava, ali se nikada ne presijeku.)
Što je asimptota logaritamske funkcije?
U ovoj jedinicu naučili smo kako je odlazak u dućan s popisom namirnica ustvari funkcija, koja može biti i ne mora biti injekcija. Za nju može i ne mora postojati inverzna funkcija.
Međutim, sada znamo da je logaritamska funkcija injekcija i da je inverz eksponencijalne funkcije. Možemo li povezati svojstva eksponencijalne i logaritamske funkcije? Što vrijedi za grafove tih funkcija? Kakvi su općenito grafovi inverznih funkcija? Na ta pitanja odgovorit ćemo u sljedećoj jedinici.
Prije nego što krenete u istraživanje tih veza, provjerite dosad stečeno znanje o logaritmima.
Ako je
koja jednakost je točna?
Odredite primjenjujući definiciju logaritma i svojstvo kompozicije inverznih funkcija.
| | |
| |
Odredite nepoznanicu
primjenjujući vezu između logaritma i potencije.
| | |
| | |
| |