

U uvodu prošle jedinice vidjeli ste gdje se sve koristi trigonometrija pravokutnog trokuta. Pozabavimo se sada iscrpnije tom temom i pogledajmo gdje se trigonometrija sve skriva. Imat ćete prigodu i isprobati trigonometriju u vlastitim malim istraživanjima, proučiti zašto se trigonometrija i astronomija vole (ljubav traje stoljećima), a možda i izabrati buduće zanimanje.
Prije nego što počnete samostalne aktivnosti i istraživanje, ponovite izračunavanje elemenata pravokutnog trokuta s pomoću sljedećega generatora zadataka. Broj zadataka je neograničen. Vježba završava kada želite ili kada su vam barem tri uzastopna zadatka točno rješena.
Napomena
Sve trigonometrijske omjere računajte na četiri decimale. Konačne rezultate zaokružite na dvije decimale i tako upišite u polje za odgovor. Kutove koji su konačni odgovor ostavite u stupnjevima i zaokružite na dvije decimale i tako upišite. Puno uspjeha.
Mjerenje visine zgrada ili planina
S pomoću trigonometrijskih omjera moguće je izmjeriti visine zgrada, planina, drveća, širinu rijeka itd. U nastavku imat ćete prigodu tu tehniku i sami isprobati u projektima.
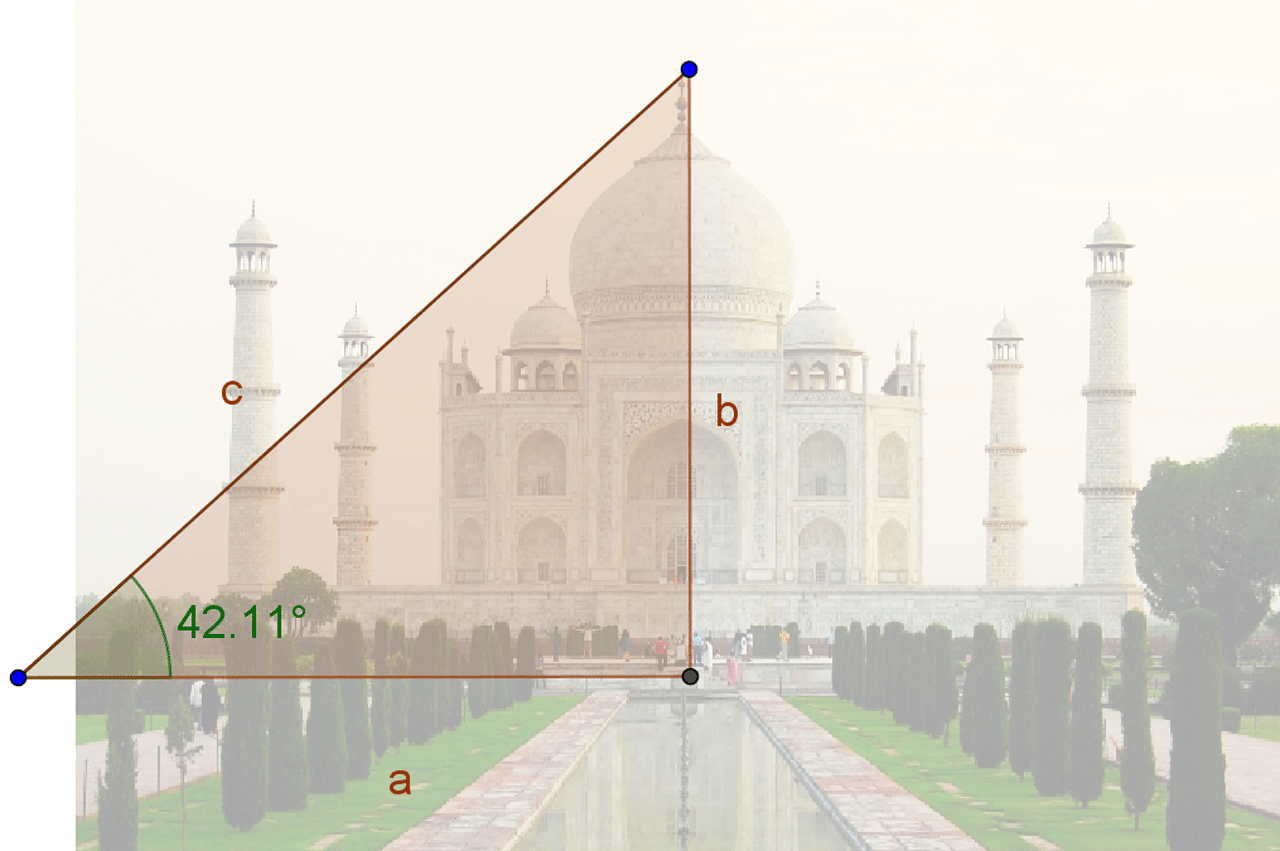

Trigonometrija u arhitekturi i građevini
Arhitekti se koriste trigonometrijom da bi izračunali nagib krova, površinu gradnje, položaj svjetla i sjene te kut pod kojim svjetlo pada.
Inženjeri građevine trebaju trigonometriju da bi izmjerili površine, postavili okomite i usporedne zidove, ugradili pločice, odredili visinu zgrade i još puno toga.

Mjeriti zgradu, drvo ili planinu možete i sami. Pred vama je projekt u kojem ćete se sami ili s prijateljima (u društvu je uvijek zabavnije) koristiti trigonometrijom pravokutnog trokuta. Projekt možete provesti korak po korak, sastavite plan rada. Ako imate volje ili prijatelja koji se bavi snimanjem ili fotografiranjem, pozovite ga da vašu avanturu dokumentira pa sve zajedno možete predstaviti u razredu.
Odaberite građevinu čiju ćete visinu mjeriti. Fotografirajte ju. Za početak riješite zadatak 1. Nakon toga odaberite dvije od ponuđenih metoda za mjerenje visine građevine i izmjerite potrebne veličine te izračunajte visinu građevine. Za zaključak komentirajte točnost pojedine metode i vezu između trigonometrije pravokutnog trokuta i zadanih metoda.
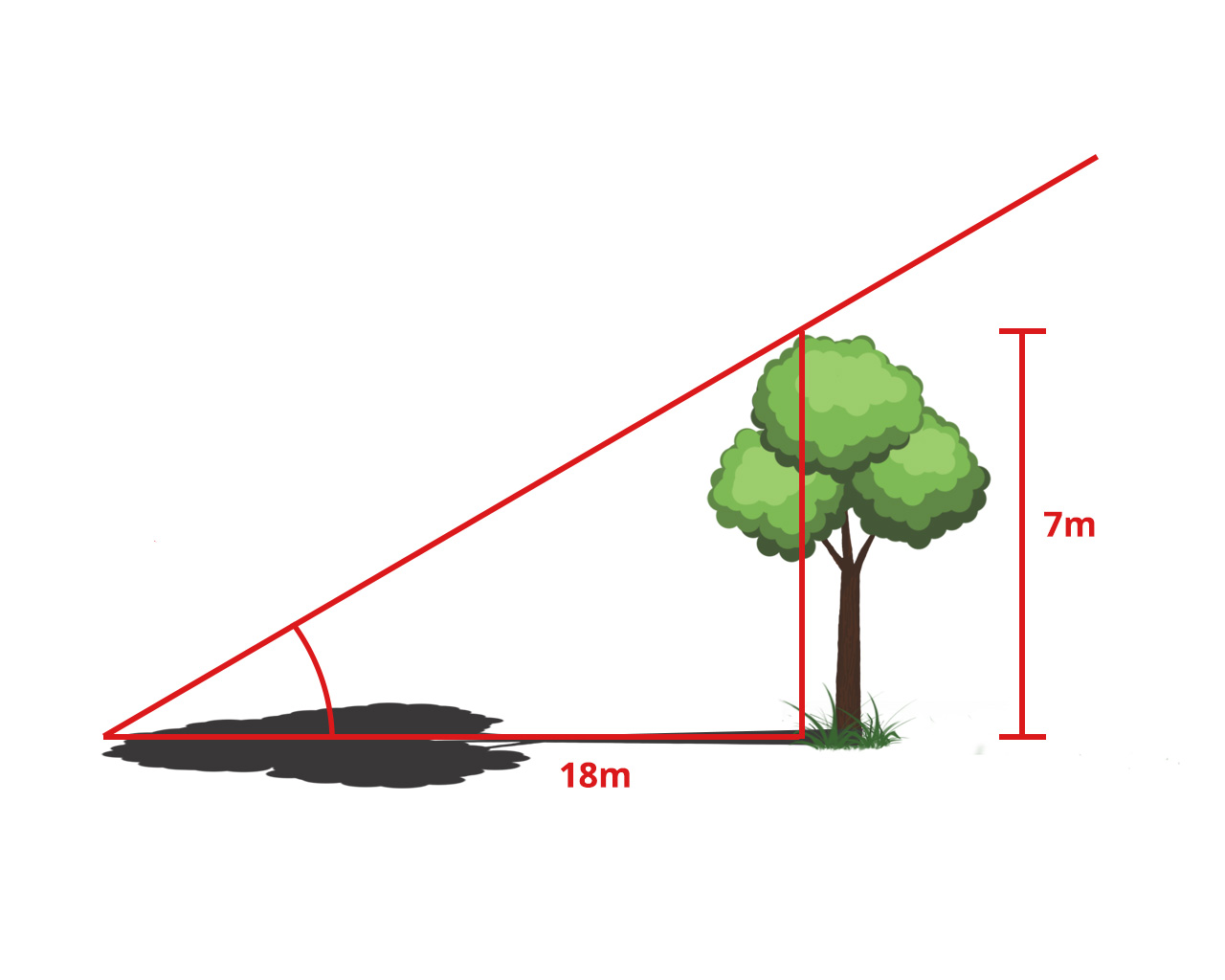
Od vrha sjene vertikalnog objekta, kao što je drvo, kut elevacije do vrha objekta jednak je kutu elevacije Sunca. Koji je kut elevacije Sunca ako drvo visine metara ima sjenu metara?
Iz trigonometrijskog omjera tangens možemo izračunati kut elevacije.

Izmjerite visinu odabrane građevine služeći se pričom o Talesu i Keopsovoj piramidi (upute ne shvaćaj doslovno te primijeni moderne materijale).
Evo jednog izvatka iz Corelusove knjige Od Pitagore do Hilberta u kojoj se opisuje postupak kojim je Tales izmjerio visinu Keopsove piramide.
„Tako on stoji u pustinjskom pijesku podno velike piramide. Jedan od svećenika smiješeći se zapita ga koliko je visoka piramida faraona Keopsa. Tales malo razmisli pa odgovori da on neće visinu cijeniti odoka, nego će je točno izmjeriti bez ikakva posebnog pribora, bez svakoga pomoćnog sredstva. Legnuo je u pijesak i odmjerio duljinu svojega tijela. — Što li to namjerava? – pitaju se svećenici. — Stat ću jednostavno – objasnio je Tales — na jedan kraj ove izmjerene dužine svojega tijela i čekat ću dok moja sjena ne bude točno onoliko duga kolika je i duljina mojega tijela. U istom trenutku mora i duljina sjene piramide vašeg faraona Keopsa iznositi točno onoliko koliko je visoka piramida. Dok je svećenik bio zabezeknut nevjerojatnom jednostavnošću rješenja, da tu nije možda pogrešan zaključak ili je riječ o nekoj varci, Tales nastavlja: — A ako hoćete da vam ovu visinu izmjerim u ma koje doba dana, tada ću zabosti ovaj štap u pijesak. Gle! – njegova sjena iznosi upravo polovinu štapa. Prema tomu, mora i sjena piramide iznositi polovinu njezine visine. Vi ste inače sposobni mjerenje izvoditi vrlo točno. Trebate samo duljinu štapa usporediti s duljinom njegove sjene pa onda, kako biste dobili visinu piramide, pomnožiti duljinu sjene piramide s dobivenim brojem.”

TEODOLIT
Teodolit je geodetski mjerni instrument za mjerenje vodoravnih kutova ili vodoravnih i okomitih kutova. Glavni su mu dijelovi vodoravni i okomiti krug s ljestvicama, dalekozor i dodatni uređaji za očitanje kutova i postavljanje u vodoravan položaj.
Prvi teodolit izađen je u Njemačkoj u 16. stoljeću.

Ako odlučimo mjeriti obližnje stablo ili neku zgradu, prvi je problem što sigurno nemamo pri ruci teodolit. Za naše mjerenje možemo se poslužiti priručnom napravom
–
klinometrom.
Riječ je o plastificiranom listu papira s pravim kutom podijeljenim na stupnjeve (ili kutomjerom) i malim viskom u vrhu pravog kuta. Za preciznije „ciljanje” na jedan je krak kuta nalijepljena slamka za pijenje.
Točne upute za izradu klinometra možete pronaći na adresi:
Sada izmjerite iz točke promatranja udaljenost građevine i kut pod kojim se vrh građevine vidi iz točke promatranja. Mjerenje ponovite najmanje pet puta i izračunajte srednju vrijednost s pogreškom.
Sada imate podatke s pomoću kojih, koristeći se trigonometrijom pravokutnog trokuta, možete izračunati visinu zgrade.
Za jedan krak kuta šestara pričvrsti se libela kako bi se postiglo da krak šestara ima vodoravan položaj. Na drugi se krak šestara pričvrsti dječji laser. Zraka lasera usmjeri se na željenu točku. Na kutomjeru šestara očita se kut, izmjeri udaljenost podnožja građevine od točke promatranja te počne računati. Mjerenje ponovite najmanje pet puta i izračunajte srednju vrijednost s pogreškom.

Kako biste saznali željeni podatak, najprije je potrebno stati na određenu udaljenost (točka promatranja) od građevine koju ćete izmjeriti s pomoću metra. Zatim kutomjerom izmjerite kut od vašeg oka do vrha tornja. Imate sve što trebate, pa počnite računati.

Trigonometrija u videoigricama
Sigurno se pitate kakve to veze ima. Svatko od vas je barem zavirio u svijet Super Maria, Sonica... Kako savršeno skakuću preko raznih zapreka, doskakuju da bi dohvatili predmete na platforme. Da bi ti naši omiljeni junaci izvodili sve te vratolomije imaju zacrtane putanje s pomoću trigonometrije. Trigonometrija je jako važna za stručnjake informatičke tehnologije (IT) u industriji videoigara.

Trigonometrija i zrakoplovi
Piloti računaju brzinu, udaljenost iz smjera i brzine vjetra. Vjetar ima važnu ulogu u tome kada i kako će zrakoplov stići na odredište. Na primjer, ako zrakoplov putuje brzinom
i to
stupnjeva od istoka prema sjeveru, a vjetar puše iz smjera juga brzinom
Trigonomerija pravokutnog trokuta pomoći će nam da nađemo treću stranu pravokutnog trokuta koja vodi zrakolov u pravom smjeru.
Na internetu pronađite smjer zrakoplova, srednju brzinu leta te brzinu i smjer vjetra za taj dan. Izračunajte smjer u kojem zrakoplov treba letjeti i kojom brzinom s pomoću vjetra.
Gdje se još trigonometrija pravokutnog trokuta pojavljuje?
Fizičari –
sjetite se gdje ste učili trigonometriju pravokutnog trokuta u fizici.
Trigonometrija i astronomija se vole. To je prava istina. Na poticaj astronoma, koji su bili i matematičari, trigonometrija se razvijala. Najviše se koristi za određivanje nemjerljivih udaljenosti i veličina objekata. Mjerenje udaljenosti je obično proces u kojem najprije mjerimo udaljenost do nekoga bliskog objekta, onda poznavanje te udaljenosti upotrebljavamo pri određivanju udaljenosti nekoga daljeg objekta, a zatim tu udaljenost koristimo za mjerenje udaljenosti još daljih objekata i tako postupno sve do kraja svemira.
Eratosten je izmjerio veličinu Zemlje. Kako je to učinio i kako vi to možete učiniti, pogledajte na adresi:
Možete li taj pokus izvesti sami ili ćete trebati pomoć?

Aristarh je mjerio udaljenost Mjeseca od Zemlje, a zatim i udaljenost Sunca od Zemlje. Izmjerite zajedno s njim udaljenost od Sunca.
Kut u vrhu u kojemu je smještena Zemlja Aristarh je izravno izmjerio i utvrdio da on iznosi
Koristeći se trigonometrijskim omjerima za pravokutni trokut, pokušajte iz navedenih kutova dobiti omjere udaljenosti do Sunca i Mjeseca te, uptrebljavajući poznatu udaljenost do Mjeseca
odredite udaljenost do Sunca. Odredite kolika je preciznost potrebna u mjerenju kuta alfa s gornje slike kako bi pogreška u određivanju udaljenosti do Sunca bila manja od
posto. Razmislite kako biste izmjerili taj kut s potrebnom preciznošću.
Najveće udaljenosti koje se još mogu određivati izravnim geometrijskim metodama su one do bližih zvijezda. Takve se zvijezde tijekom godine, zbog gibanja Zemlje oko Sunca, prividno pomiču po nebeskom svodu, tj. relativno s obzirom na udaljene zvijezde. Mjereći te pomake, to jest tzv. kut paralakse može se odrediti udaljenost do zvijezde.
Promatrajući prividni pomak zvijezde na svemirskom svodu šest mjeseci moguće je odrediti tzv. paralaksu te zvijezde, to jest kut Uz znanje udaljenosti Zemlje od Sunca ( astronomska jedinica) s pomoću trigonometrije možete odrediti udaljenosti do zvijezde.
Za kut koji iznosi sekundi, pronađi udaljenost pripadajuće zvijezde.

Trigonometrija pravokutnog trokuta prati nas i u matematici. Od velike je pomoći kod geometrijskih tijela. Pokrenite animaciju u 3D-u uz sljedeće upute:
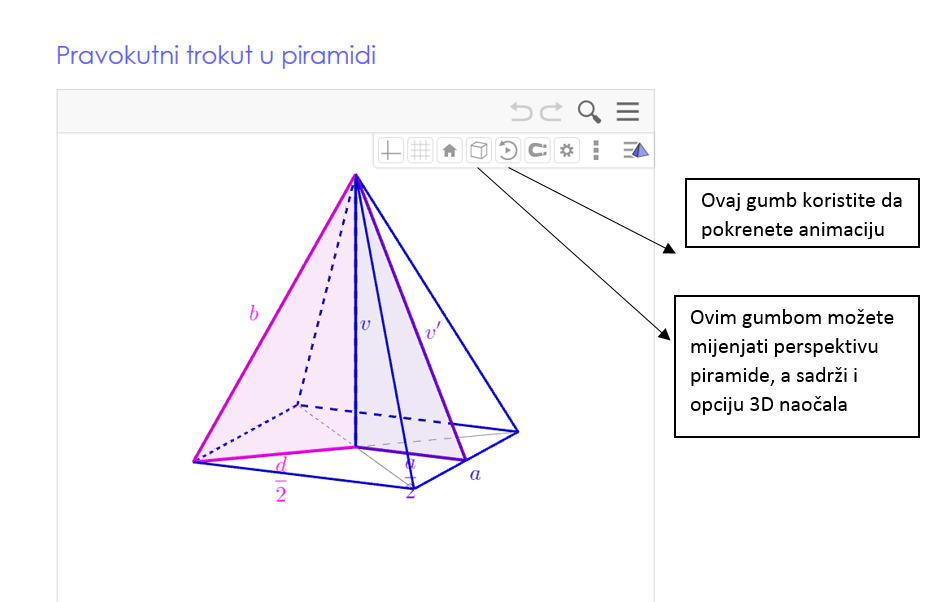
Uočite dva pravokutna trokuta s pomoću kojih se može izračunati visina piramide i visina bočne stranice piramide. Možete li izvesti formule?
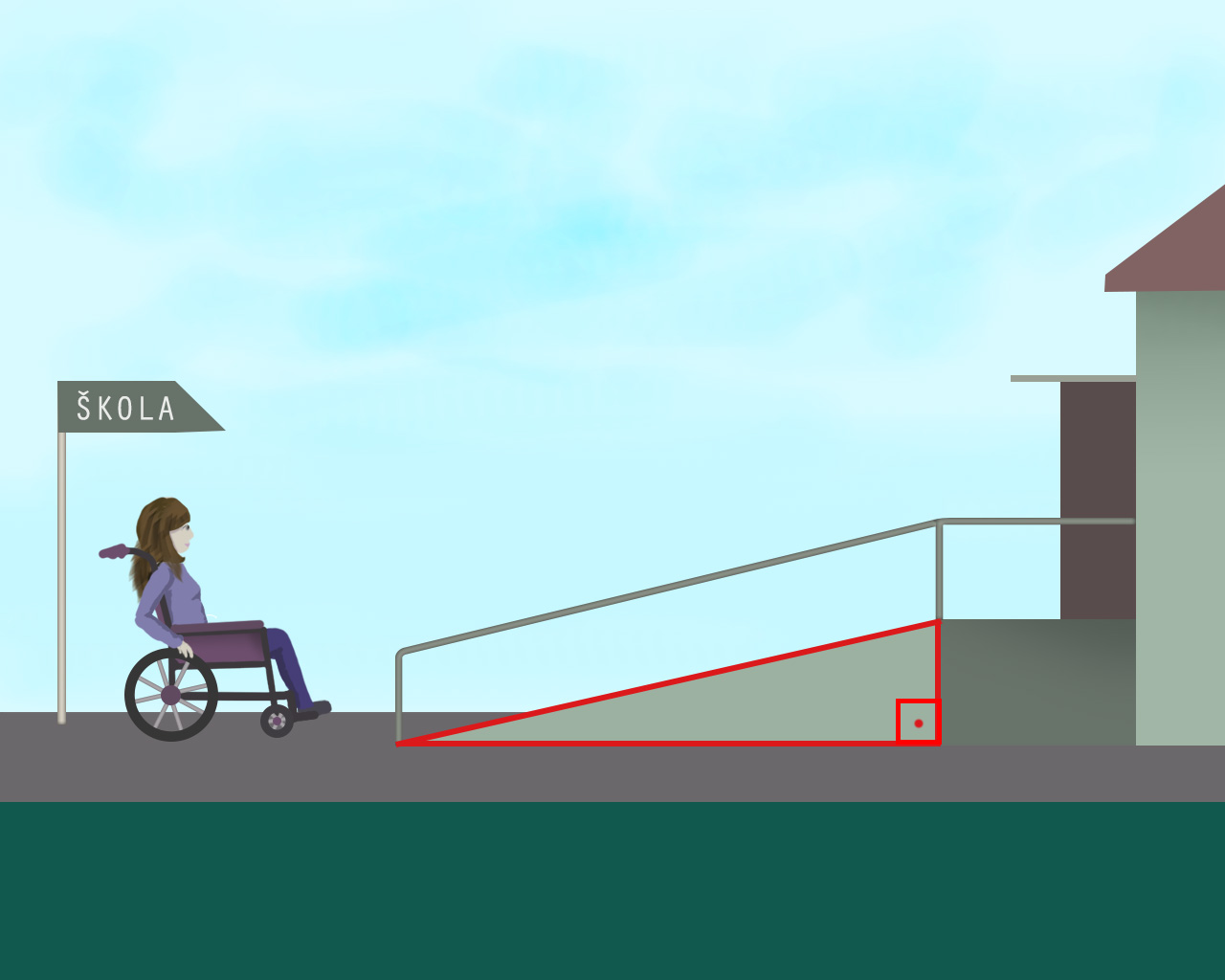
Na linku pronađite dokument iz kojeg donosim izvadak o uvjetima koje treba zadovoljavati rampa za invalide:
„Rampa se koristi kao element pristupačnosti za svladavanje visinske razlike do uključivo 120 cm, u unutarnjem ili vanjskom prostoru. Rampa mora omogućavati ispunjavanje sljedećih uvjeta, odnosno imati:
Koliko je trigonometrije u tom izvadku? Zašto je nagib važan?
Napiši u bilježnici scenarij za izgradnju rampe za invalide u svojoj zgradi ili, ako rampa postoji, provjeri zadovoljava li uvjete.
I za kraj malo matematičke čarolije. Otkrit ćemo tajnu koju ste vidjeli, ali niste dokazali u 4.3. Ali vi i dalje možete zadiviti svoje prijatelje.
Sve što trebate je uočiti pravokutne trokute i izmjeriti katete. Duljina kateta pravokutnog trokuta na dijelu čokolade koji se ne lomi ne mijenja se, ali izmjerite katete gornjeg dijela. Kad s pomoću tangensa izračunate kut jednog i drugog pravokutnog trokuta, vidjet ćete da se kutovi razlikuju. To znači da ni hipotenuze nisu jednake, a mala razlika neće biti previše vidljiva kao pukotina, i to je tajna naše matematičke čarolije.
A višak čokolade možete pojesti.