

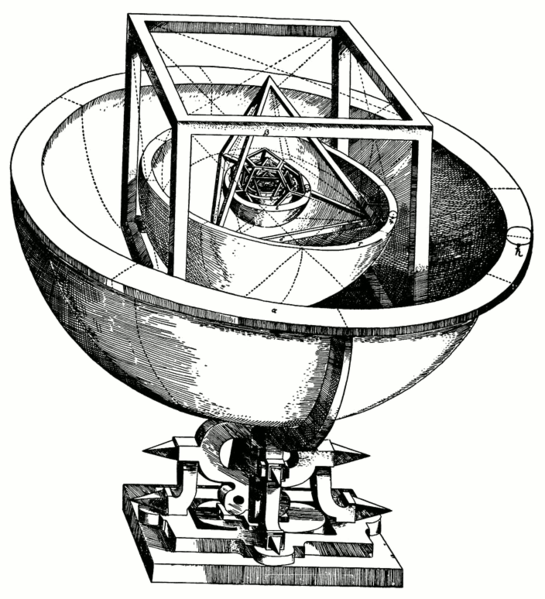
Slika prikazuje model Sunčeva sustava iz Keplerove knjige Kozmičke tajne (1596.). Kepler smješta Sunce u središte svih sfera po kojima se gibaju svi planeti i time se izjašnjava kao zagovornik heliocentričnog sustava. Utvrdio je da bi svako od pet Platonovih tijela moglo biti jedinstveno umetnuto u sferu. Oko sfere po kojoj se giba Merkur opiše se oktaedar, oko tog oktaedra sfera na kojoj se nalazi Venera, a oko te sfere opisuje se ikosaedar oko kojega je sfera na kojoj se nalazi Zemlja. Zatim ide dodekaedar sa sferom na kojoj se giba Mars pa tetraedar na sferi Jupitera i na kraju kocka sa sferom na kojoj se nalazi Saturn, posljednji tada Kepleru poznat planet.

Johannes Kepler (1571.-1630.), njemački je astronom, matematičar i astrolog. Ustanovio je gibanje planeta po elipsama te time srušio vjerovanja da se planeti oko Sunca gibaju po kružnicama. Keplerova kozmološka teorija temelji se na kopernikanskom sustavu u kojem pet pravilnih poliedara određuje strukturu svemira i odražava božanski plan u geometriji.
Jesu li vam poznati istaknuti pojmovi? Ovdje se spominje pet pravilnih poliedara, odnosno Platonovih tijela. Što su Platonova tijela, odnosno pravilni poliedri? Znate li opisati svaki od njih i objasniti zašto se tako zovu?
Da bismo ovo lakše razumjeli i definirali, moramo, uz osnovne pojmove stereometrije s kojima ste se upoznali u jedinici 8.1 Abeceda stereometrije, ponoviti i definirati još nekoliko pojmova.
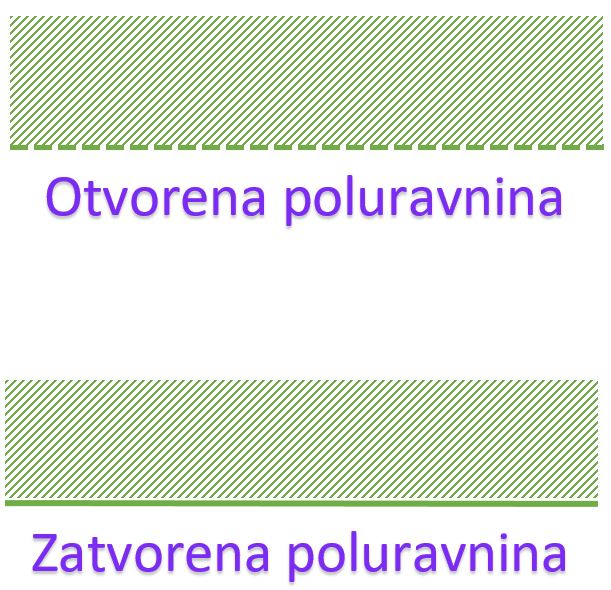
Poluravnina je skup svih točaka ravnine koje se nalaze s jedne strane nekog pravca te ravnine.
Svaki pravac dijeli ravninu na tri dijela: pravac i dvije poluravnine.
Poluravnina može biti otvorena i zatvorena. Poluravnina je zatvorena ako sadrži pravac. Tada je pravac rub zatvorene poluravnine.
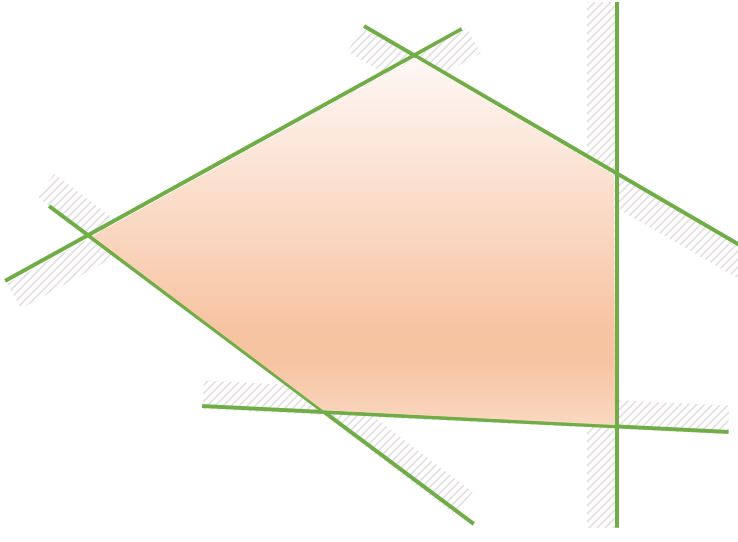
Konveksni mnogokut (poligon) omeđeni je skup u ravnini dobiven kao presjek konačno mnogo poluravnina.
Mnogokut kojemu su sve stranice jednake i svi kutovi jednaki zove se pravilni mnogokut.
Ponovimo nekoliko pojmova ravnine.
Koji se maksimalni konveksni
-terokut može dobiti ako se sijeku četiri različite poluravnine?
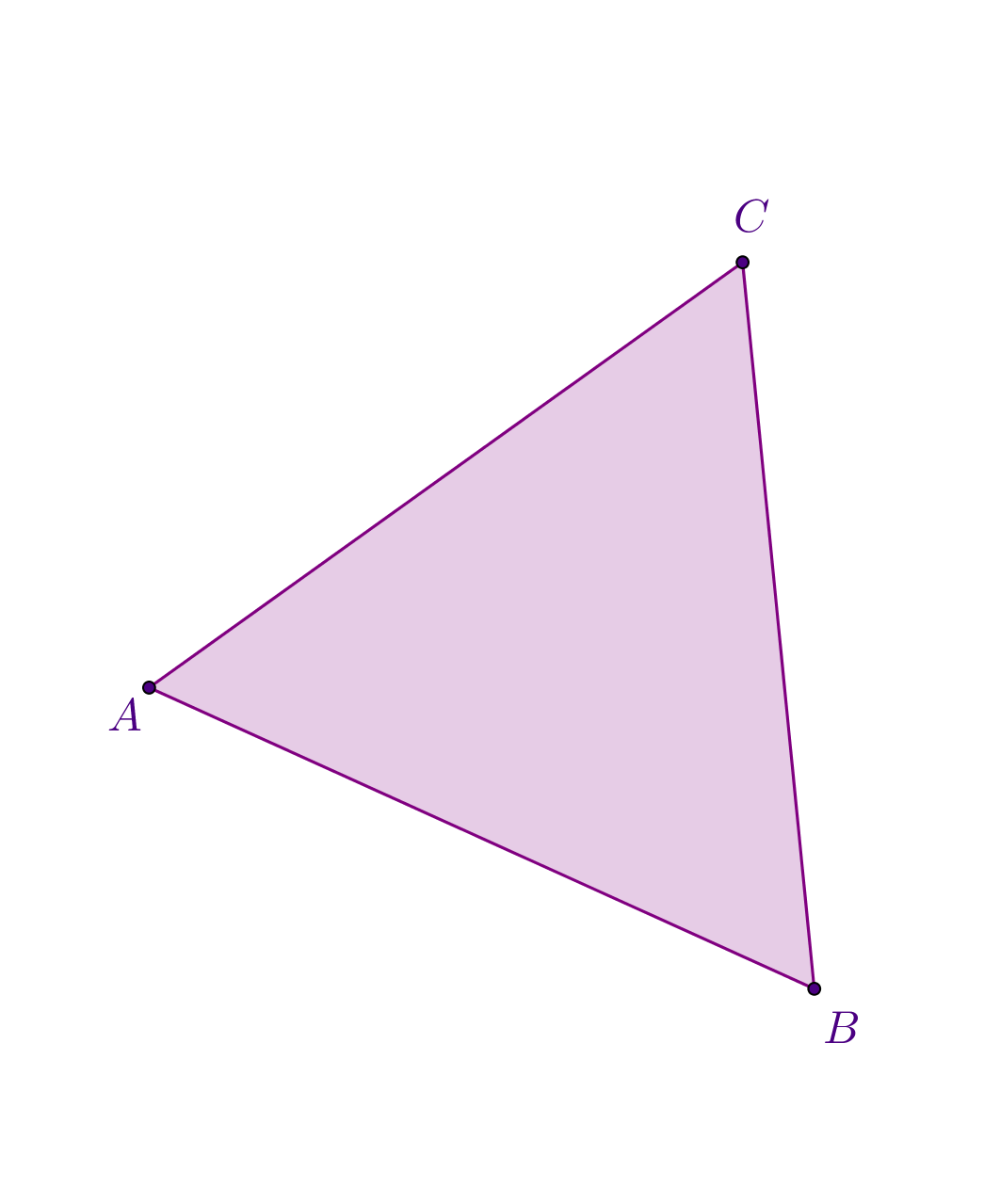
Konveksni mnogokut ne mora biti zadan presjekom konačno mnogo poluravnina.
Zadajmo tri nekolinearne točke Njima je jednoznačno određena ravnina. Koji je najmanji konveksni skup koji ih sadrži?
Po definiciji, konveksni skup mora sadržavati spojnice svakih dviju točaka toga skupa, a najmanji takav upravo je skup točaka unutar spojnica
Dužine
Općenito, najmanji konveksni skup koji sadrži konačno mnogo točaka koje nisu kolinearne konveksni je mnogokut. Zadane točke vrhovi su mnogokuta, osim onih točaka koje se nalaze unutar tog mnogokuta ili na njegovoj stranici.
Konveksnom mnogokutu (poligonu) svaki je unutarnji kut manji od:
Povežite pojmove s pripadajućim formulama.
|
Zbroj unutarnjih kutova
-terokuta
|
|
|
Broj dijagonala
-terokuta
|
|
|
Broj karakterističnih trokuta pravilnog
-terokuta
|
|
|
Mjera kuta nasuprot osnovici
karakterističnog trokuta
pravilnog
-terokuta
|
|
|
Mjera unutarnjeg kuta pravilnog
-terokuta |
|
Potražimo pojmove u prostoru koji su analogoni pojmovima u ravnini.
Znate li definirati pojam geometrije? Ponovimo definicije pojmova povezanih s geometrijom likova i tijela.
Planimetrija je grana geometrije koja se bavi geometrijskim likovima u ravnini i njihovim odnosima.
Pojam planimetrije nastaje u starogrčkoj matematici iako se elementi planimetrije javljaju i prije. Starogrčki znanstvenici i pisci smatrali su da je Egipat kolijevka geometrije.
Naziv (lat. planus - ravan i grč. μετρεω - mjera) nastao je u europskoj srednjovjekovnoj matematici.
Naziv stereometrija prvi se put pojavljuje kod Aristotela.
Dolazi od grčkih riječi στερεoξ (stereos) - prostor i μετρεω (metreo) - mjera.
Stereometrija je grana geometrije koja proučava geometrijska tijela i njihove odnose u trodimenzionalnom prostoru.
Geometrija (mjerstvo) grana je matematike koja se bavi prostornim odnosima i oblicima.
Povežite planimetrijske pojmove sa stereometrijskim analogonima.
|
pravca/poluravnine određuju najmanji konveksni mnogokut
|
Konveksni poliedar |
|
Konveksni mnogokut
|
Ravnina |
|
Pravac
|
ravnine/poluprostora određuju najmanji konveksni poliedar |
|
Poluravnina
|
Poluprostor |
Pokušajmo naći analogiju s planimetrijom kod stereometrijskih pojmova.
Sama riječ geometrija doslovno označava "mjerenje zemlje". Dolazi od grčih riječi γεα (gea) - zemlja i
μετρεω (metreo) - mjera.
Prema Herodotu, egipatska geometrija nastala je zbog potrebe mjerenja zemljišnih parcela, što je bilo često kod Egipćana zbog poplava Nila. U daljnjem razvoju geometrija je otišla mnogo dalje od mjerenja zemlje i postala dio matematike koji proučava svojstva i odnose oblika. Za samo mjerenje zemlje već je Aristotel uveo drugi naziv - "geodezija".
Poluprostor je skup svih točaka prostora koje se nalaze s iste strane neke ravnine tog prostora.
Svaka ravnina dijeli prostor na tri dijela: ravninu i dva poluprostora.
Presjeci poluprostora konveksni su skupovi. Mogu biti omeđeni ili neomeđeni.
U kakvom položaju mogu biti dvije, odnosno tri ravnine prostora?
Dvije ravnine u prostoru mogu:
Tri ravnine u prostoru mogu biti u jednom od pet mogućih položaja:
Primjer 1.
Što dobijemo presjekom tih ravnina? Kada su dobiveni skupovi točaka omeđeni? Nacrtajmo položaje tih ravnina.
Dvije paralelne ravnine dijele prostor na tri dijela od kojih su dva dijela , a treći je .
Koji od položaja triju različitih ravnina u prostoru kao presjek ima omeđeni skup (konveksni poliedar)?
Vidjeli smo da nam tri ravnine nisu dovoljne da dobijemo omeđeni konveksni skup u prostoru. Moramo uzeti bar četiri ravnine da dobijemo omeđeni skup kao presjek poluprostora.
Konveksni poliedar omeđeni je skup u prostoru dobiven kao presjek konačno mnogo poluprostora.
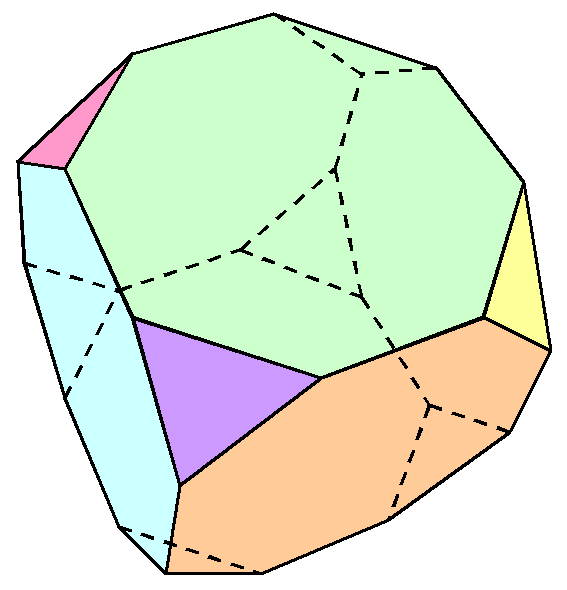
Strane poliedra konveksni su mnogokuti, dio ravnine koji odsijecaju preostale ravnine. Ravnine se sijeku po pravcu. Dijelovi pravaca koji su zajednički za ravnine koje se sijeku čine rubove tih konveksnih mnogokuta. To su bridovi poliedra. Pravci se sijeku u točki. Presjeci pravaca su vrhovi poliedra. Pomoću strana, bridova i vrhova opisujemo poliedar.
Strane poliedra mnogokuti su koji omeđuju poliedar.
Bridovi poliedra stranice su mnogokuta koji omeđuju poliedar.
Vrhovi poliedra vrhovi su mnogokuta koji omeđuju poliedar.
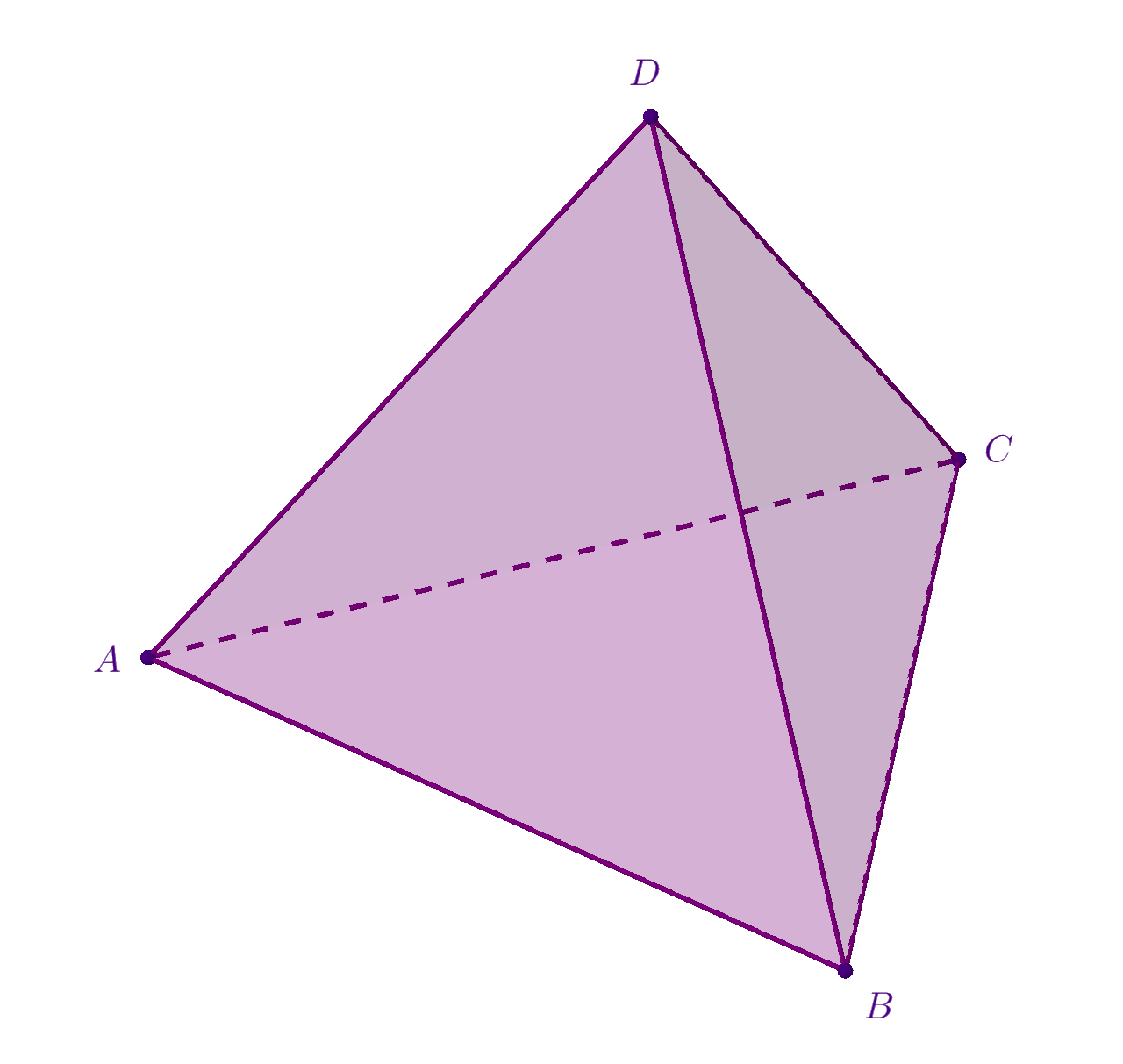
Konveksni poliedar možemo zadati nekomplanarnim točkama kao i u ravnini konveksni mnogokut nekolinearnim točkama (najmanje tri). Što je analogon trokutu u dimenziji više? Zadajmo četiri nekomplanarne točke Što su spojnice tih točaka? Bridovi kojeg poliedra?
U skladu s definicijom konveksnog poliedra najmanji konveksni skup u prostoru koji je određen s četirima točkama naziva se tetraedar. Spojnice naših četiriju točaka bridovi su tetraedra, odnosno bridovi konveksnog poliedra. Sve ostale spojnice leže ili na stranama tetraedra ili unutar njega. Tetraedar se može dobiti i kao presjek četiriju poluprostora određenih ravninama zadanih točaka
Općenito, za zadani konačni skup nekomplanarnih točaka, najmanji konveksni skup koji ih sadrži naziva se konveksni poliedar. Zadane točke čine vrhove poliedra, osim onih koje leže na bridu poliedra, na njegovoj strani ili unutar njega.
Označimo broj vrhova poliedra s broj bridova s i broj strana poliedra sa Bez obzira na različitosti poliedara, jedno im je svojstvo svima zajedničko, veza između broja vrhova, bridova i strana poliedra.
Zbroj broja vrhova i broja strana za svaki poliedar za dva je veći od broja njegovih bridova, tj. vrijedi Eulerova formula
Još u 18. stoljeću formulu je otkrio švicarski matematičar i fizičar Leonhard Euler. Dokaza Eulerove formule ima mnogo. Prvi precizan dokaz u 18. stoljeću dao je Adrien Marie Legendre, francuski matematičar i astronom, a zatim početkom 19. stoljeća Augustin Louis Cauchy, još jedan francuski matematičar.
Primjer 2.
Provjerimo istinitost Eulerove formule kod tetraedra.
Uvrštavanjem u lijevu stranu Eulerove formule za
,
i
dobijemo
što je i trebalo dokazati.
Provjerite istinitost Eulerove formule kod sljedećih geometrijskih tijela.
Koliko
-terostrana
prizma ima vrhova, strana i bridova?
| |
Koliko
-terostrana piramida ima vrhova, strana i bridova?
i
Provjerite Eulerovu formulu za
-terostranu prizmu i piramidu.
Uvrštavanjem dobivenih stranica, vrhova i bridova u Eulerovu formulu za piramidu, dobivamo
Analogno tomu, provjerite za prizmu.

Neke podatke o poliedrima poznavali su još stari Egipćani. Konstrukcija pet pravilnih poliedara pripisuje se Pitagori. Pitagorejci su u svojim kozmološkim teorijama davali posebno mjesto pravilnim poliedrima.
Učenje o pravilnim poliedrima sadržano je u XIII. knjizi Euklidovih Elemenata u kojoj on dokazuje da postoji samo pet pravilnih poliedara.
Nakon Biblije Elementi su najviše proučavano, tiskano i prevođeno djelo.
Posebno su kroz povijest bili zanimljivi poliedri kojima su strane pravilni mnogokuti.
Geometrijsko (konveksno) tijelo koje je omeđeno sukladnim pravilnim mnogokutima i kojemu iz svakog vrha izlazi jednak broj bridova zove se pravilni poliedar.
Pravilnih poliedara ili Platonovih tijela ima točno pet, što se može pokazati pomoću Eulerove formule i definicije pravilnog poliedra. Pogledajmo nazive, broj strana, vrhova i bridova svakog od tih pet pravilnih poliedara te
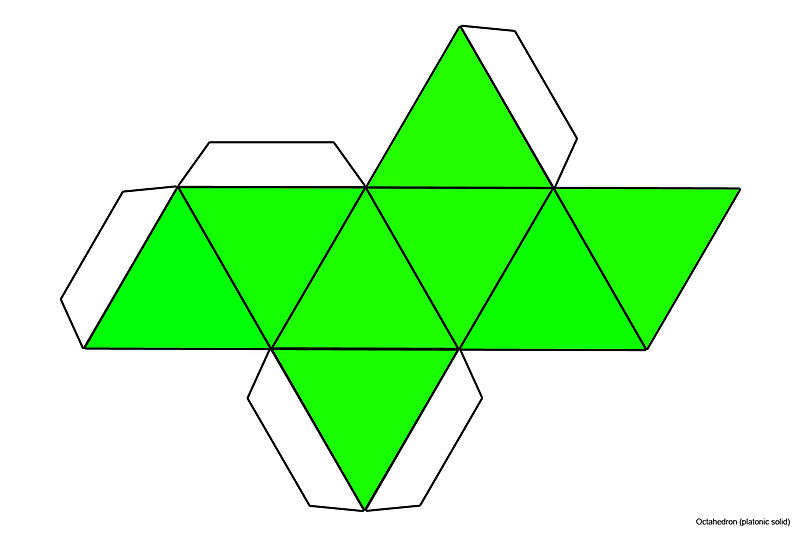
broj pravilnih mnogokuta koji se sijeku u svakom vrhu. Nacrtajmo ih kao i pripadajuću mrežu.
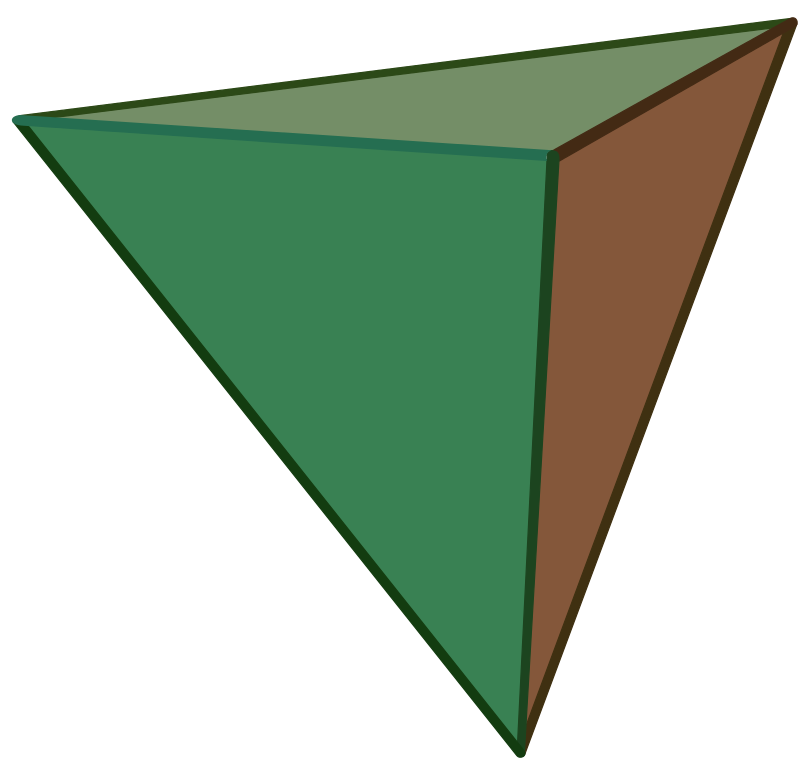
Pravilni tetraedar (grč. tetra - četiri)
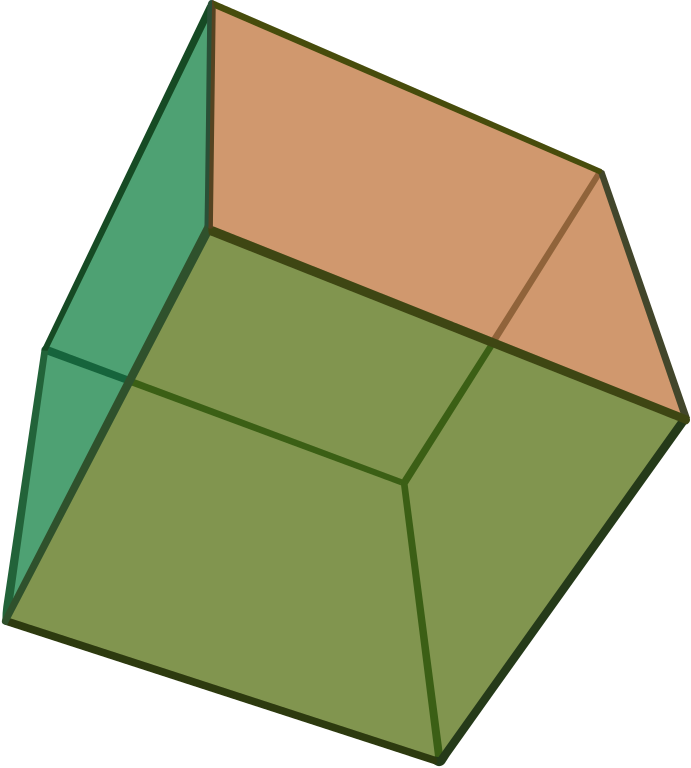
Pravilni heksaedar (kocka) (grč. heksa - šest)
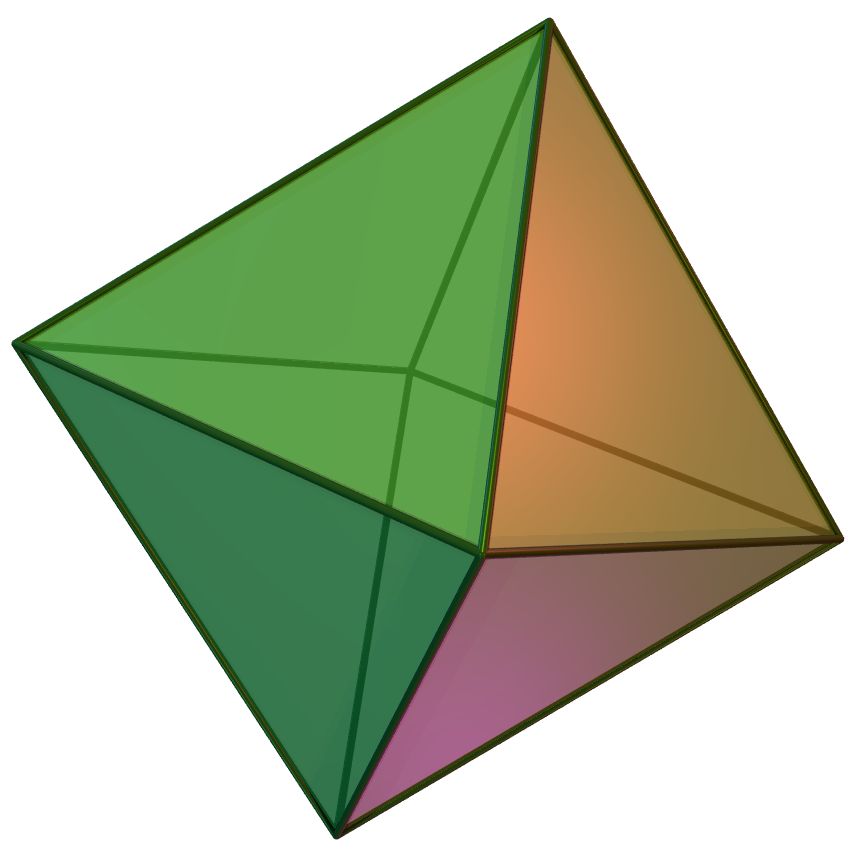
Pravilni oktaedar (grč. okto - osam)
Pravilni dodekaedar (grč. dodeka - dvanaest)
Pravilni ikosaedar (grč. ikosi - dvadeset)
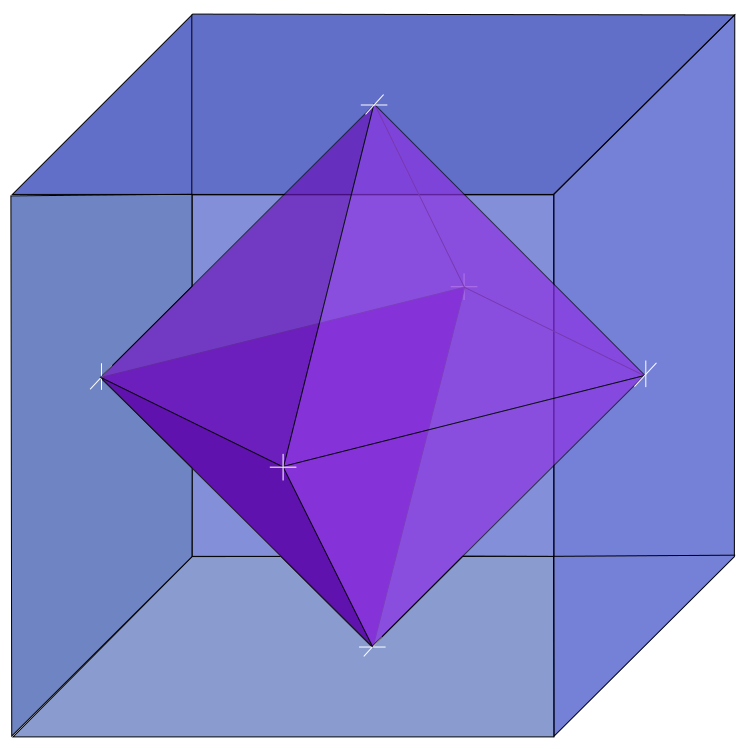
Pravilni poliedri imaju zanimljivo svojstvo dualnosti. Pravilni ikosaedar i pravilni dodekaedar međusobno su dualni. Središta strana pravilnog ikosaedra vrhovi su pravilnog dodekaedra i obrnuto. Isto su tako kocka i oktaedar međusobno dualna tijela. Tetraedar je dualan sam sebi. Zaključite u kakvoj su vezi broj vrhova i broj strana dualnih poliedara.
Pravilnih poliedara ima u prirodi.
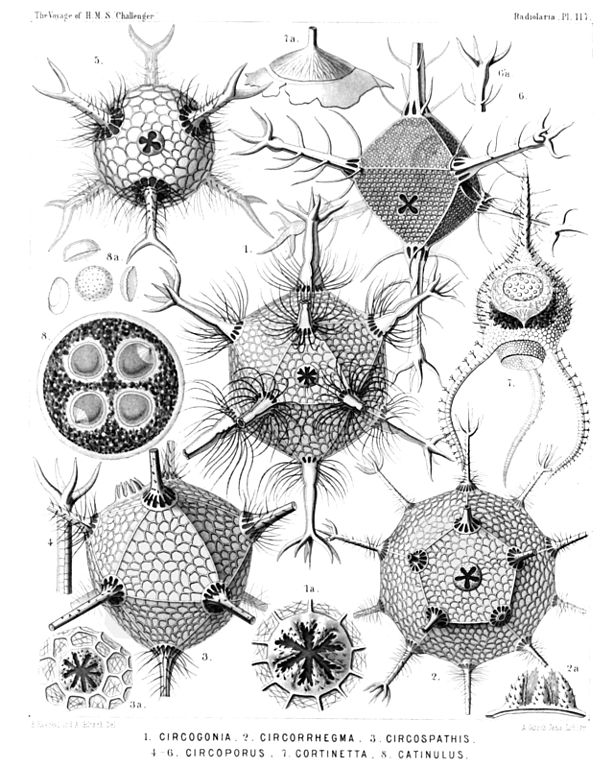
Kostur jednostaničnog organizma zrakaša (lat. Circogonia icosahedra) u obliku je ikosaedra.
(Slika 1)
Većina ih živi duboko u vodi i plijen su koraljnim ribama. Zato se pokušavaju obraniti pomoću dvanaest šupljih bodlji iz dvanaest vrhova kostura. S nastavnicima iz biologije napravite malo istraživanje o ovom jednostaničnom organizmu. Potražite još organizama koji u prirodi imaju oblik Platonovih tijela.
Neki virusi kao što je virus herpesa imaju oblik pravilnog ikosaedra. Istražite zbog čega.
Kristalne rešetke minerala imaju oblik Platonovih tijela.
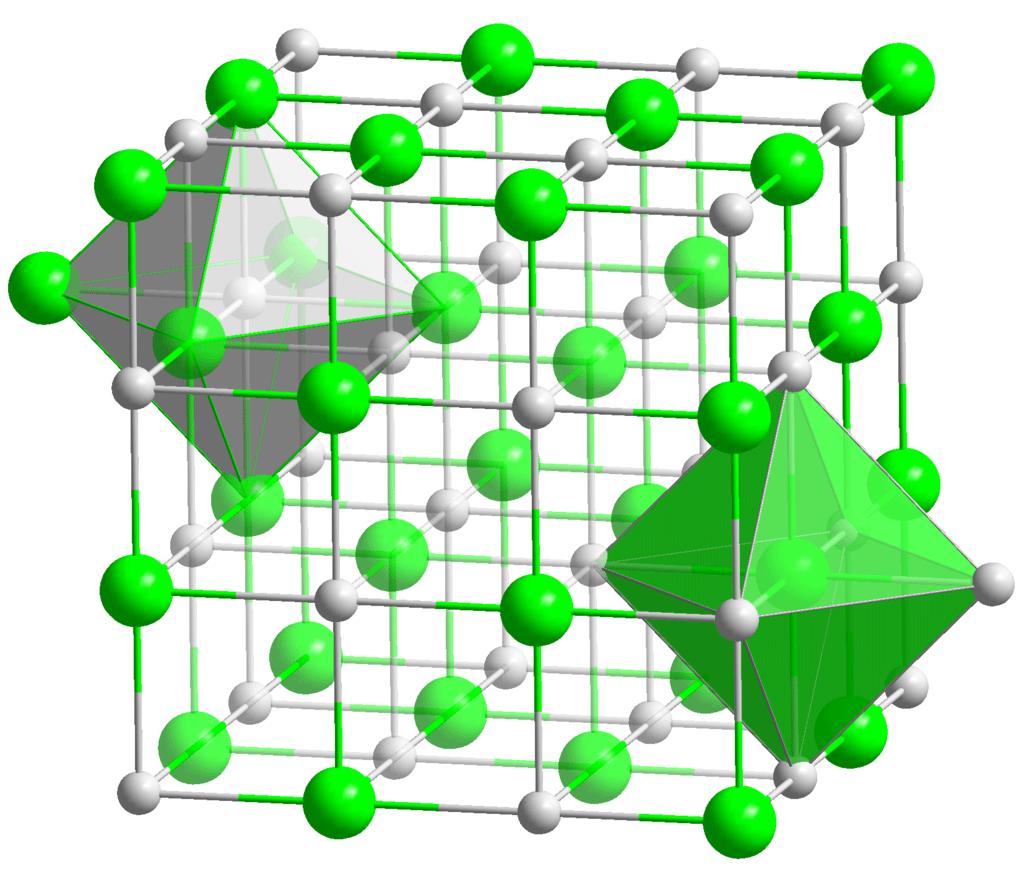
Koje pravilne poliedre sadrži kristalna struktura kuhinjske soli? (Slika 2)
Koju strukturu ima pirit, mineral sumpora? (Slika 3)

Za razliku od pravilnih poliedara kojih je samo pet, postoje i polupravilni poliedri ili Arhimedova tijela. To su poliedri od kojih je svaki omeđen pravilnim poligonima drugačijeg tipa i kojima su sukladni poliedarski kutovi i istoimeni poligoni. Ima ih Broj strana tih poliedara je između i Istražite i napravite prezentaciju o Arhimedovim polupravilnim tijelima.
Albrecht Dürer (1471.-1528.), njemački slikar i kipar, pravio je od papira pravilne i polupravilne poliedre. Nacrtao je njihove mreže i savio ih u poliedar. Pokušajte i sami napraviti što više poliedara. Iskušajte se i u tehnici origamija.
Johannes Kepler (1571.-1630.) opisao je dva pravilna nekonveksna poliedra - veliki i mali zvjezdasti dodekaedar. Dva stoljeća poslije, Louis Poinsot (1777.-1859.), francuski matematičar i fizičar, opisuje još dva zvjezdasta pravilna nekonveksna poliedra - veliki dodekaedar i veliki ikosaedar. Po njima su dobili naziv Kepler-Poinsotova tijela. Cauchy je dokazao da postoje samo četiri takva pravilna nekonveksna poliedra.

Pravilni poliedri su kroz povijest bili inspiracija mnogim znanstvenicima, filozofima i umjetnicima. Pitagorejci im daju prednost pred drugima baš zbog toga što ih je samo pet. U antičkoj filozofiji osnovnima su se smatrala četiri elementa prirode: zemlja, voda, zrak i vatra. Starogrčki filozof Platon davao je atomima tih elemenata formu tetraedra (zemlja), kocke (voda), oktaedra (zrak) i ikosaedra (vatra). Formu dodekaedra Platon je davao cijelom svijetu. Otuda alternativni nazivi za pravilne poliedre (kozmičke figure, idealne figure, Platonova tijela).
Pravilnim su poliedrima često bili zaokupljeni i umjetnici. Poznati su crteži poliedara Leonarda da Vincija koje je pravio za rukom pisano izdanje De divina proportione (Božanski omjer) fra Luce Paciolija. Salvador Dali, katalonski slikar, posljednju je večeru smjestio u prostor pravilnog dodekaedra.