Matematika 2 - 2.8 Bikvadratne jednadžbe

Na početku...

Naučili smo rješavati kvadratnu jednadžbu. Prokušajmo riješiti sljedeći zadatak.

Zbroj kvadrata duljina stranica pravokutnika je $18 .$ Odredi duljine stranica pravokutnika ako je površina $9 .$

Pomičući točku B mijenjaj duljine stranica pravokutnika.

Primjer 1.

Oznake: $a,$ $b$ - duljine stranica pravokutnika.

Poznato: zbroj kvadrata duljina stranica je $18$

$a^{2} + b^{2} = 18 .$

Površina pravokutnika je $9 .$ Površina pravokutnika jednaka je produktu duljina stranica.

$a \cdot b = 9 .$

Nepoznato: duljine stranica pravokutnika: $a, b .$

Da bismo izračunali duljine stranica potrebno je riješiti sustav od dviju jednadžbi s dvije nepoznanice.

$a^{2} + b^{2} = 18$

$a \cdot b = 9$

Postoji li uvijek jedinstveno rješenje sustava od dviju jednadžbi s dvije nepoznanice?

Sustav neće uvijek imati jedinstveno rješenje.

Pomoć:

Rješavanje sustava od dviju linearnih jednadžbi s dvije nepoznanice objašnjeno je u Matematici 1, modul 7 i Matematici 7, modul 9.

null

Rješavanje sustava od dviju linearnih jednadžbi s dvije nepoznanice objašnjeno je u Matematici 7 i Matematici 1. Vidjeli smo da sustav neće uvijek imati jedinstveno rješenje. U prethodnoj jedinici rješavali smo sustave linearne i kvadratne jednadžbe.

Pripadaju li sustavi $a^{2} + b^{2} = 18$ i $a \cdot b = 9$ u sustave linearne i kvadratne jednadžbe?

Ovdje su navedene dvije kvadratne jednadžbe.

null

Pokušajmo riješiti i ovu vrstu sustava. Analogno kao i kod sustava linearne i kvadratne jednadžbe pokušat ćemo upotrijebiti metodu supstitucije.

$a^{2} + b^{2} = 18$ i

$a \cdot b = 9 \Rightarrow a = \frac{9}{b}$

Uvrštavanjem izraza $a = \frac{9}{b}$ u prvu jednadžbu dobivamo

$(\frac{9}{b})^{2} + b^{2} = 18$

$\frac{81}{b^{2}} + b^{2} = 18.$

Množenjem s $b^{2}$ dobijemo jednadžbu $81 + b^{4} = 18 b^{2} .$ Prebacimo li sve članove na lijevu stranu i posložimo ih po potencijama, od b dobijemo $b^{4} - 18 b^{2} + 81 = 0 .$ Ova jednadžba podsjeća na kvadratnu, ali to nije kvadratna jednadžba.

Bikvadratna jednadžba

Jednadžba oblika $a x^{4} + b x^{2} + c = 0$ naziva se bikvadratna jednadžba.

Kako ćemo riješiti bikvadratnu jednadžbu? Možemo li od bikvadratne jednadžbe dobiti kvadratnu?

Supstitucijom

t = x^{2}

Možemo supstitucijom

t = x^{2}

null

Supstituiramo li $t = x^{2}$ bikvadratna jednadžba prelazi u kvadratnu.

Uvrštavanjem $t = b^{2}$ u jednadžbu $b^{4} - 18 b^{2} + 81 = 0$ dobivamo kvadratnu jednadžbu $t^{2} - 18 t + 81 = 0 .$ Ta kvadratna jednadžba ima samo jedno rješenje $t = 9 .$ Ako to rješenje vratimo u našu supstituciju $b^{2} = t,$ dobit ćemo $b^{2} = 9,$ odnosno $b_{1} = 3, b_{2} = - 3 .$ Naravno, duljina stranice nije negativan broj, pa je $b = 3 .$ Iz $a = \frac{9}{b}$ dobijemo da je $a = 3 .$ Dakle, pravokutnik kojem su duljina stranica $a$ i $b$ jednake (kvadrat) i iznose $3,$ zadovoljava uvjete da je zbroj kvadrata duljina stranica $18,$ a površina $9 .$

Bikvadratne jednadžbe su jednadžbe oblika $a x^{4} + b x^{2} + c = 0 .$ Rješavamo ih uvođenjem zamjene (supstitucijom) $t = x^{2,}$ čime bikvadratna jednadžba prelazi u kvadratnu $a t^{2} + b t + c = 0 .$

Zanimljivost

Naziv bikvadrat dolazi od dviju latinskih riječi:

bi - (lat. bis) predmetak u složenicama koji kazuje da se značenje drugog dijela složenice pojavljuje dvaput

kvadrat – (lat. quadratum) matematička jednadžba drugog stupnja (kod koje nepoznata veličina stoji na drugoj potenciji).

Primjer 2.

Riješimo jednadžbu:

$36 x^{4} - 25 x^{2} + 4 = 0 .$

Rješenje je prikazano u videu koji slijedi.

Kutak za znatiželjne

Grafički prikaz bikvadratne funkcije $f (x) = 36 x^{4} - 25 x^{2} + 4$ u koordinatnom sustavu izgleda ovako:

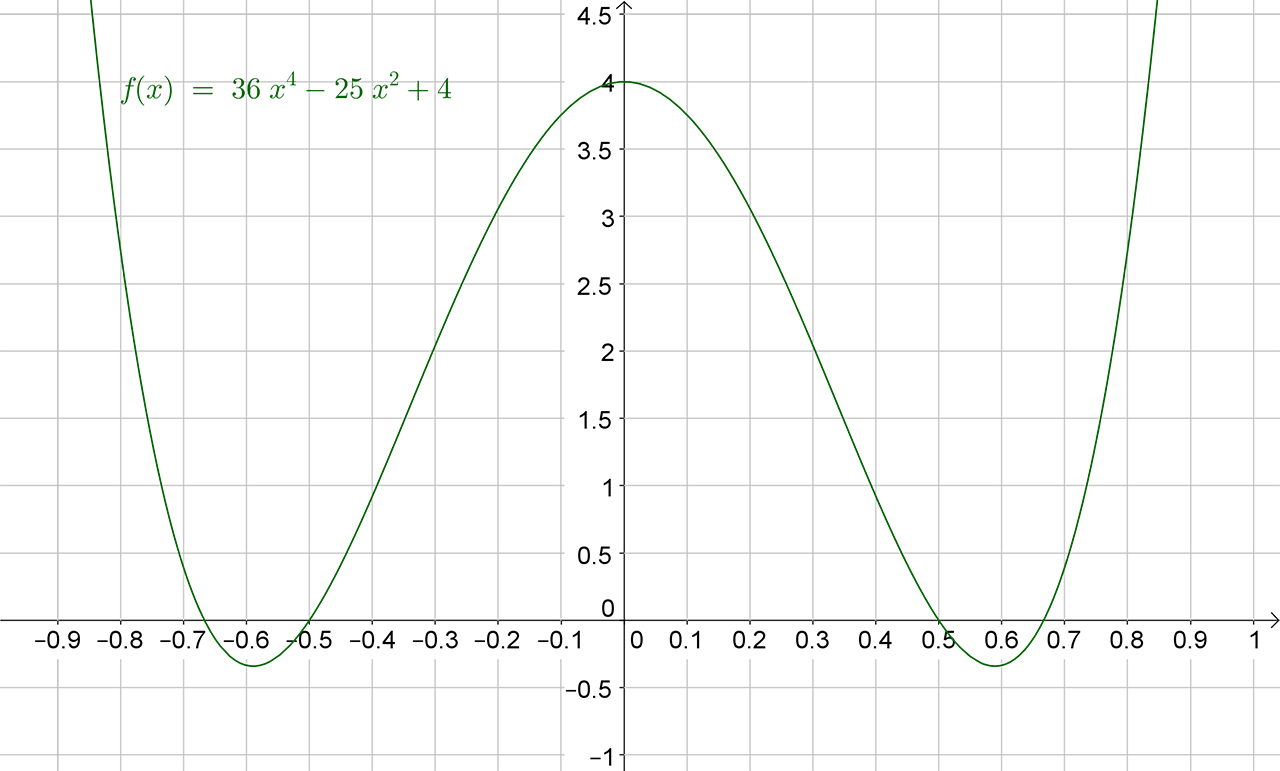
Grafički prikaz bikvadratne funkcije

Rješenja bikvadratne jednadžbe su nultočke funkcije čiji je grafički prikaz na slici. Iz grafičkog prikaza mogu se naslutiti rješenja

$x_{1} = - \frac{2}{3}, x_{2} = - \frac{1}{2}, x_{3} = \frac{1}{2}, x_{4} = \frac{2}{3} .$

Primjer 3.

Riješimo bikvadratnu jednadžbu: $x^{4} + 3 x^{2} - 4 = 0 .$

Uvrštavanjem supstitucije $t = x^{2}$ bikvadratna jednadžba prelazi u kvadratnu $t^{2} + 3 t - 4 = 0 .$ Rješenja ove kvadratne jednadžbe su: $t_{1} = 1$ i $t_{2} = - 4 .$ Dobivena rješenja uvrstimo u $t = x^{2}$ i dobivamo dvije kvadratne jednadžbe $x^{2} = 1$ i $x^{2} = - 4 .$

Iz prve jednadžbe, $x^{2} = 1,$ dobijemo rješenja za x: $x_{1} = 1, x_{2} = - 1 .$

Rješenja druge jednadžbe, $x^{2} = - 4,$ su $x_{3} = 2 i, x_{4} = - 2 i .$

Rješenja bikvadratne jednadžbe

Spojite bikvadratne jednadžbe s njihovim rješenjima.

$x^{4} + 8 x^{2} + 16 = 0$	$x_{1} = 3 i, x_{2} = - 3 i, x_{3} = 2 i, x_{4} = - 2 i$
$x^{4} + 4 x^{2} = 0$	$x_{1} = 2 i, x_{2} = - 2 i$
$x^{4} - 13 x^{2} + 36 = 0$	$x_{1} = 0, x_{2} = 2 i, x_{3} = - 2 i$
$x^{4} - 5 x^{2} - 36 = 0$	$x_{1} = 3, x_{2} = - 3, x_{3} = 2 i, x_{4} = - 2 i$
$x^{4} + 13 x^{2} + 36 = 0$	$x_{1} = 3, x_{2} = - 3, x_{3} = 2, x_{4} = - 2$

null

U prethodnom zadatku imali smo nekoliko sličnih bikvadratnih jednadžbi s različitim brojem i vrstom rješenja.

Koliko najviše različitih rješenja može imati bikvadratna jednadžba?

1

2

4

8

null

Bikvadratna jednadžba može imati najviše četiri različita rješenja. Rješenja mogu biti realna i kompleksna. Kompleksna rješenja uvijek se pojavljuju u parovima – konjugirano kompleksni brojevi.

Kolekcija zadataka 1

Zadatak 1.

Odredite vrijednost realnog parametra $p$ za koji će jednadžba $x^{4} - 2 x^{2} + p = 0$ imati samo dva realna (dvostruka) rješenja.

$p = 1$

Uputa: diskriminanta bikvadratne jednadžbe treba biti $0 .$

Zadatak 2.

Odredite bikvadratnu jednadžbu čija su rješenja $x_{1} = 3,$ $x_{2} = - 3,$ $x_{3} = 1,$ $x_{4} = - 1 .$

$\begin{array}{l} (x - 3) (x + 3) (x - 1) (x + 1) = 0 \end{array}$

$x^{4} - 10 x^{2} + 9 = 0$

Zatvori

...i na kraju

Bikvadratne jednadžbe su jednadžbe oblika

a x^{4} + b x^{2} + c = 0 .

Rješavamo ih uvođenjem zamjene (supstitucijom)

t = x^{2}

čime bikvadratna jednadžba prelazi u kvadratnu

a t^{2} + b t + c = 0 .

Bikvadratna jednadžba može imati najviše četiri rješenja.

$\|x + 2\| (x - 1) = 0$	$x_{1} = 2, x_{2} = 2, x_{3} = i, x_{4} = - i$
$x^{4} - 3 x^{2} - 4 = 0$	$x_{1} = \frac{1}{2}, x_{2} = - 2$
$(2 x - 1) (x + 2) = 0$	$x_{1} = 1, x_{2} = - 1$
$x^{4} - 2 x^{2} + 1 = 0$	$x_{1} = 1, x_{2} = - 2$

2.8 Bikvadratne jednadžbe

Na početku...

Bikvadratna jednadžba

Zanimljivost

Kutak za znatiželjne

Rješenja bikvadratne jednadžbe

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

...i na kraju

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

2.9 Primjena kvadratnih jednadžbi