


Ponovimo.
U idućoj animaciji pratite položaj pravca u odnosu na ravninu te uočite u kojem sve odnosu mogu biti pravac i ravnina. Kvadar i ravninu možete rotirati držeći lijevu tipku miša.
Pravac i ravnina u prostoru su ili paralelni ili se sijeku u jednoj točki. Pritom paralelnost uključuje i slučaj kad pravac leži u ravnini.
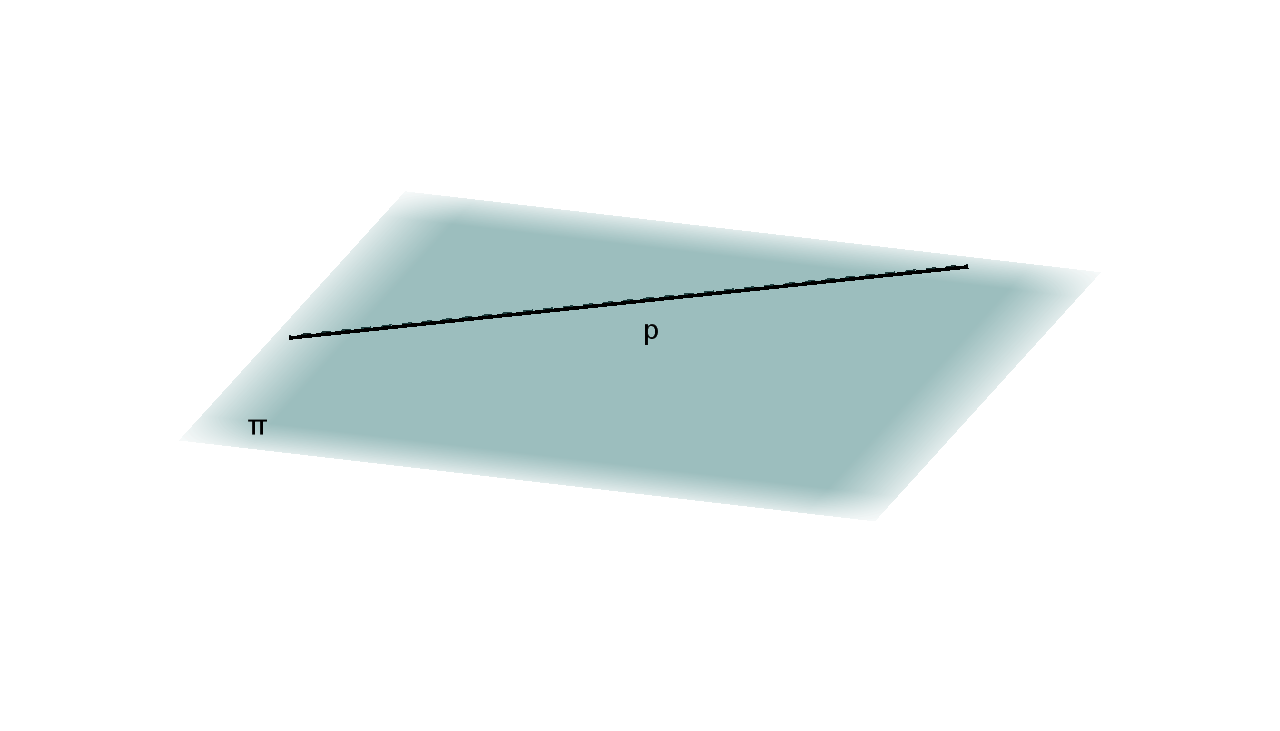
a. Svaka točka pravca ujedno je i točka ravnine. Situacija kada pravac leži u ravnini zapisuje se
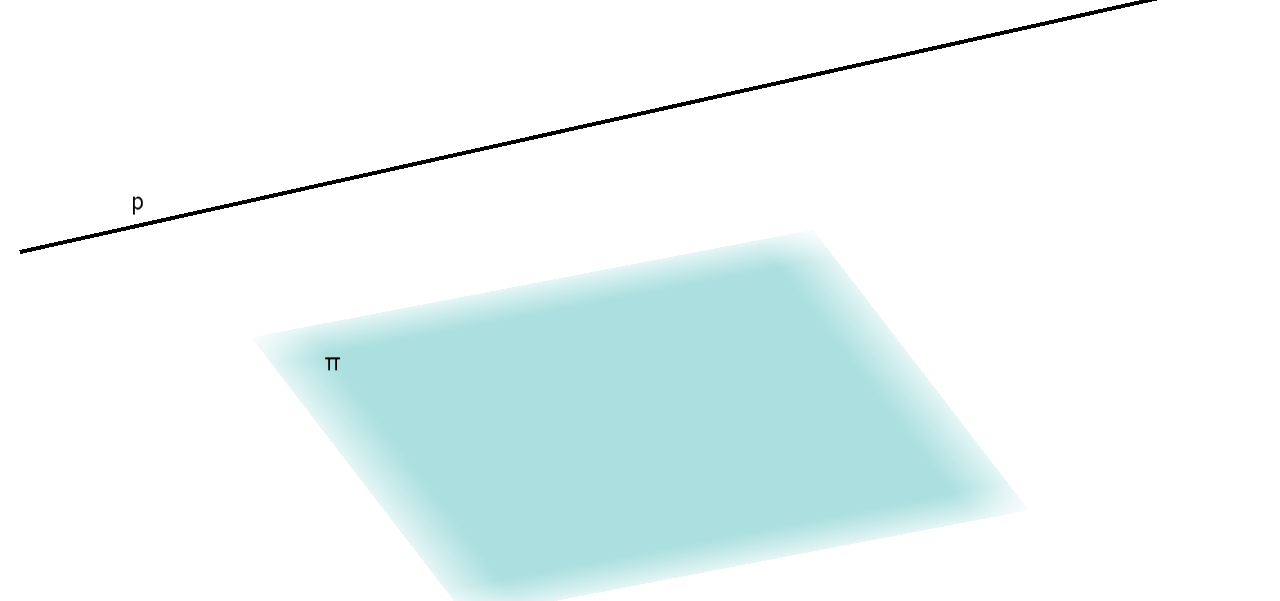
b. Ako pravac i ravnina nemaju presječnih točaka, kažemo da su paralelni. Pišemo:

c. Ako se pravac i ravnina sijeku, tada imaju samo jednu presječnu točku. Pišemo: Točka naziva se sjecište ili probodište pravca i ravnine.
U idućoj animaciji pratite položaj ravnina u odnosu na istaknutu ravninu te uočite u kojem sve odnosu mogu biti.
Dvije ravnine u prostoru mogu biti ili paralelne ili je njihov presjek pravac. Pritom paralelnost uključuje slučaj kad se ravnine podudaraju.

a. Dvije se ravnine podudaraju ako imaju barem tri zajedničke nekolinearne točke. Pišemo:

b. Dvije su ravnine paralelne ako se podudaraju ili ako se ne sijeku. Pišemo:
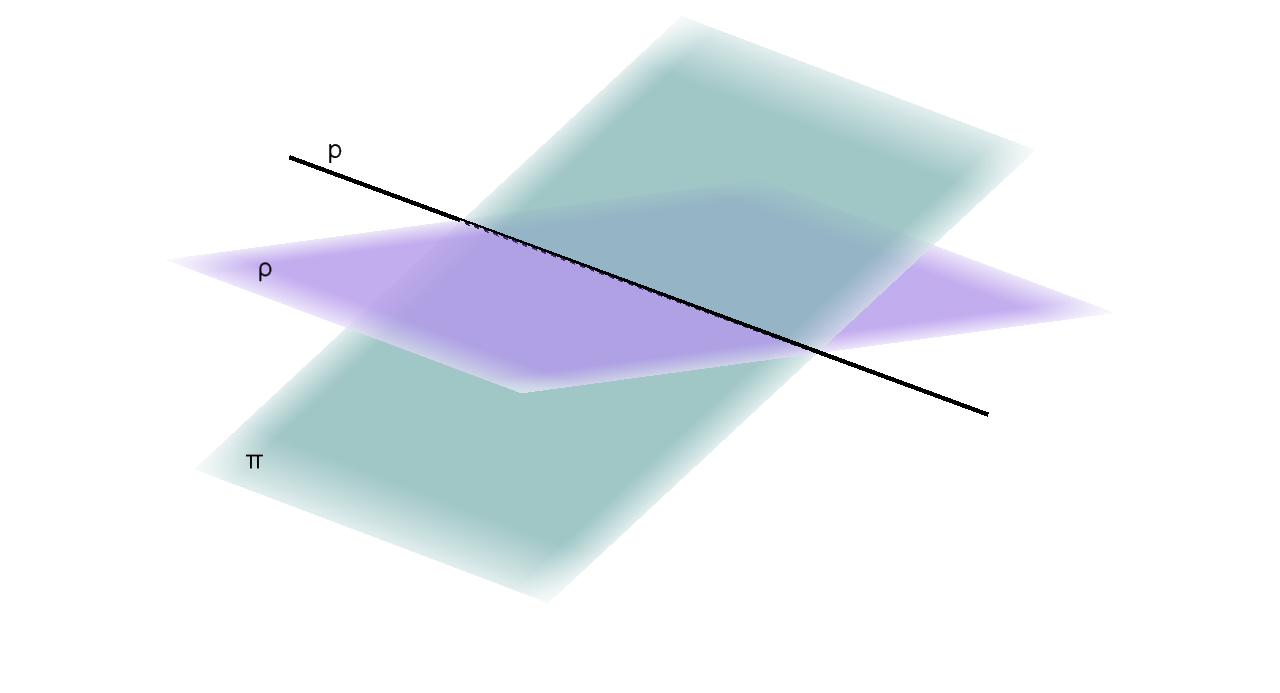
c. Dvije ravnine koje imaju zajedničkih točaka, a ne podudaraju se, sijeku se po pravcu. Pišemo:
Presjek dviju ravnina u prostoru može biti:
Postoje i višedimenzionalni prostori. Istražite mogu li se u višedimenzionalnom prostoru dvije ravnine sjeći u samo jednoj točki.
Tri ravnine u prostoru mogu biti u jednom od pet mogućih položaja:
- postoji samo jedna točka zajednička za sve tri ravnine
- sve tri ravnine sijeku se duž jednog pravca
- po dvije se ravnine sijeku u trima paralelnim pravcima
- dvije su ravnine paralelne, a treća ih siječe duž dvaju paralelnih pravaca
- sve su tri ravnine paralelne.
Razmislite kako bi ti položaji izgledali te ih skicirajte na plakatu. Pokušajte izraditi modele od kartona ili šperploče koji bi prikazivali moguće položaje triju ravnina u prostoru.
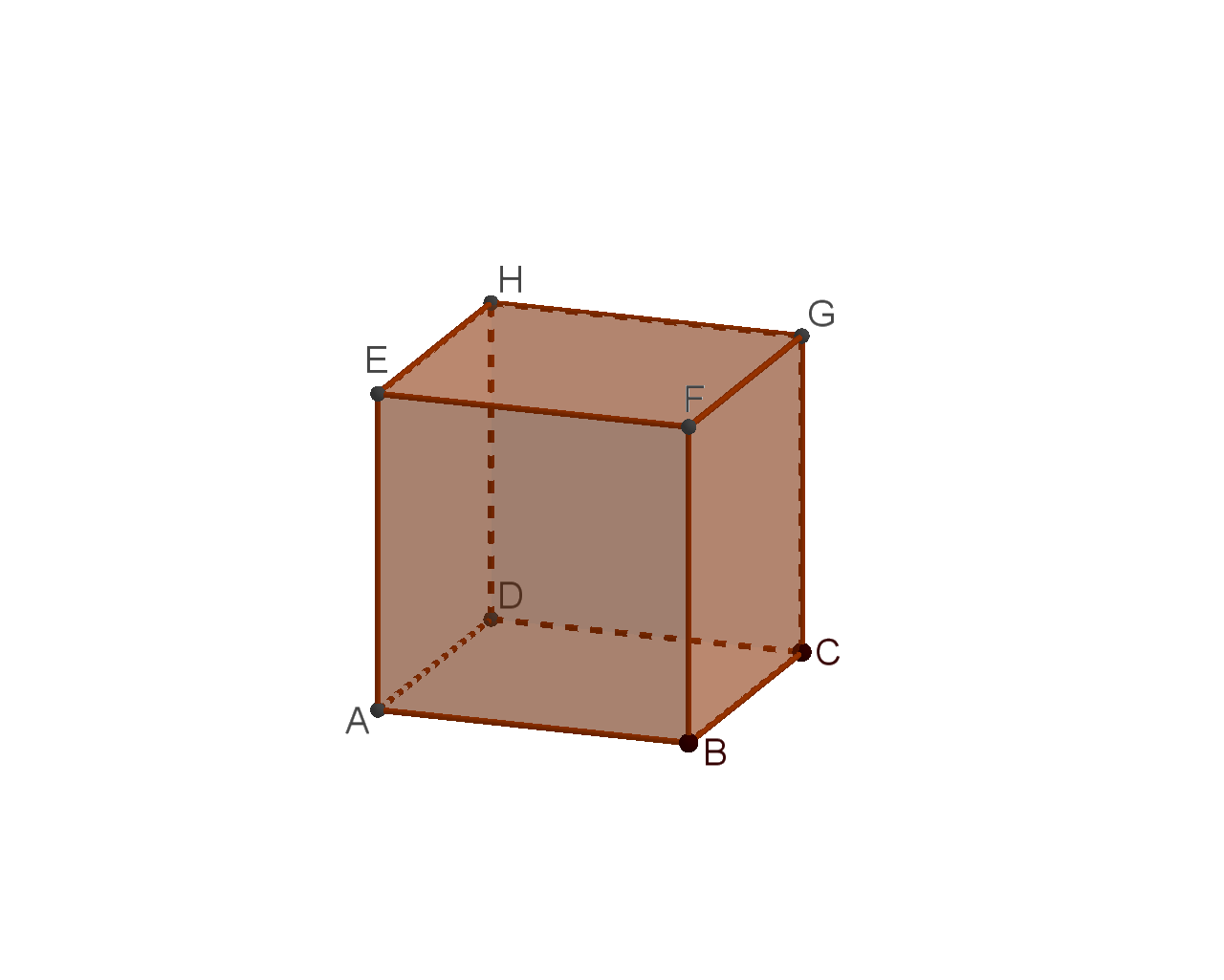
Pogledajte kocku pa odgovorite u kojem su položaju:
Dvije su ravnine paralelne ako nemaju zajedničkih točaka. Također se smatra da je ravnina paralelna sama sa sobom.

Pravac i ravnina su paralelni ako nemaju zajedničkih točaka. Također se smatra da je pravac paralelan s ravninom koja ga sadrži.
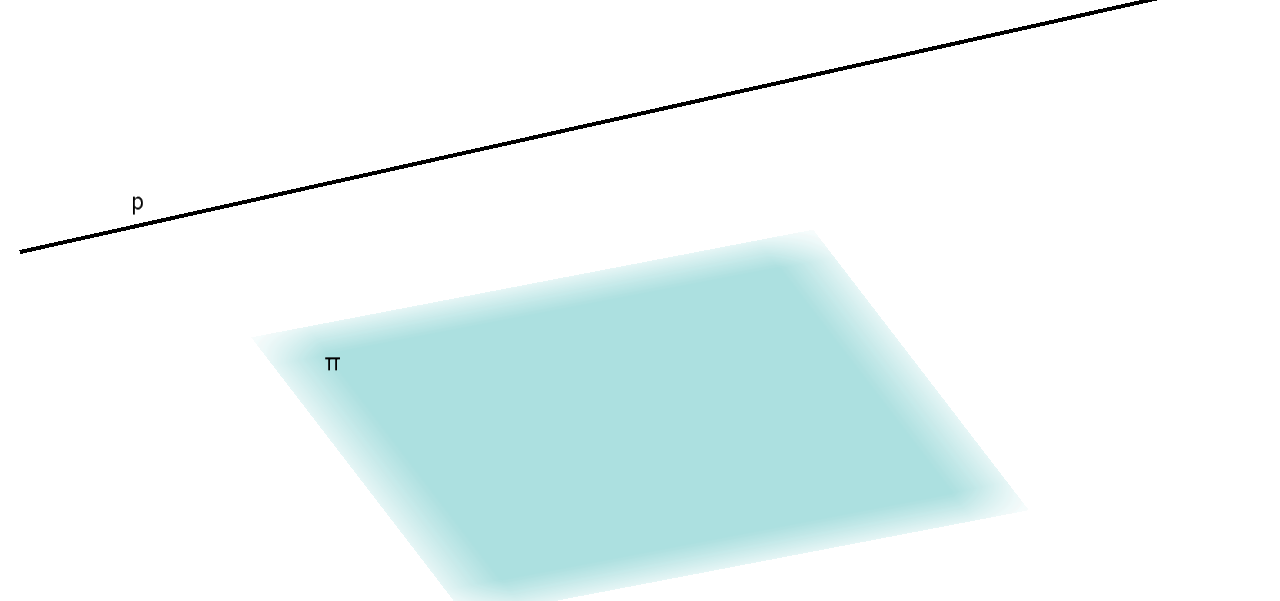
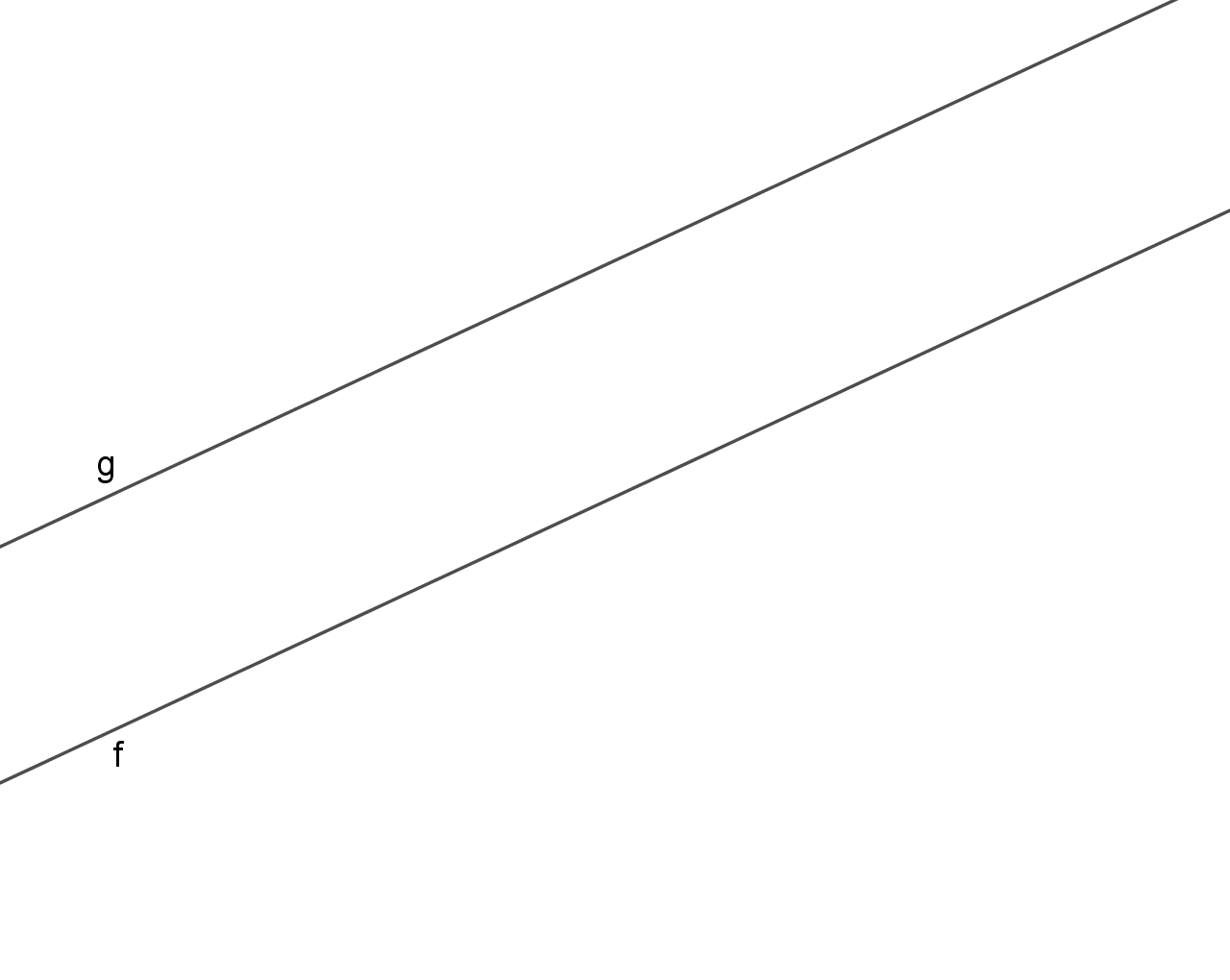
Dva su pravca paralelna ako leže u istoj ravnini i nemaju zajedničkih točaka. Također se smatra da je svaki pravac paralelan sam sa sobom.
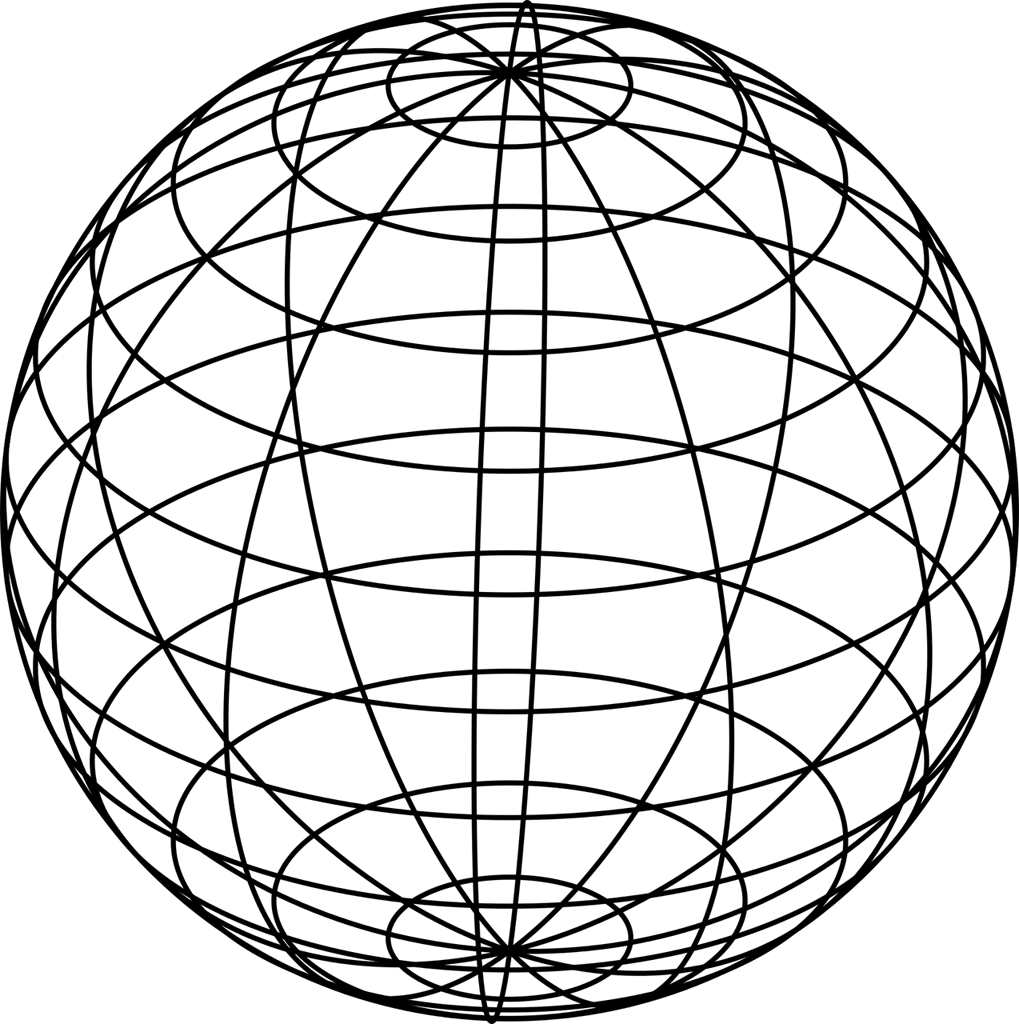
Sferna geometrija vrsta je neeuklidske geometrije na sferi za koju su pravci glave kružnice sfere, točke su točke sfere, a ravnina je zadana sfera. U sfernoj geometriji nije zadovoljen Euklidov aksiom o paralelama, svaka dva pravca sijeku se u dvije točke pa točkom izvan pravca ne prolazi niti jedan pravac paralelan sa zadanim pravcem.
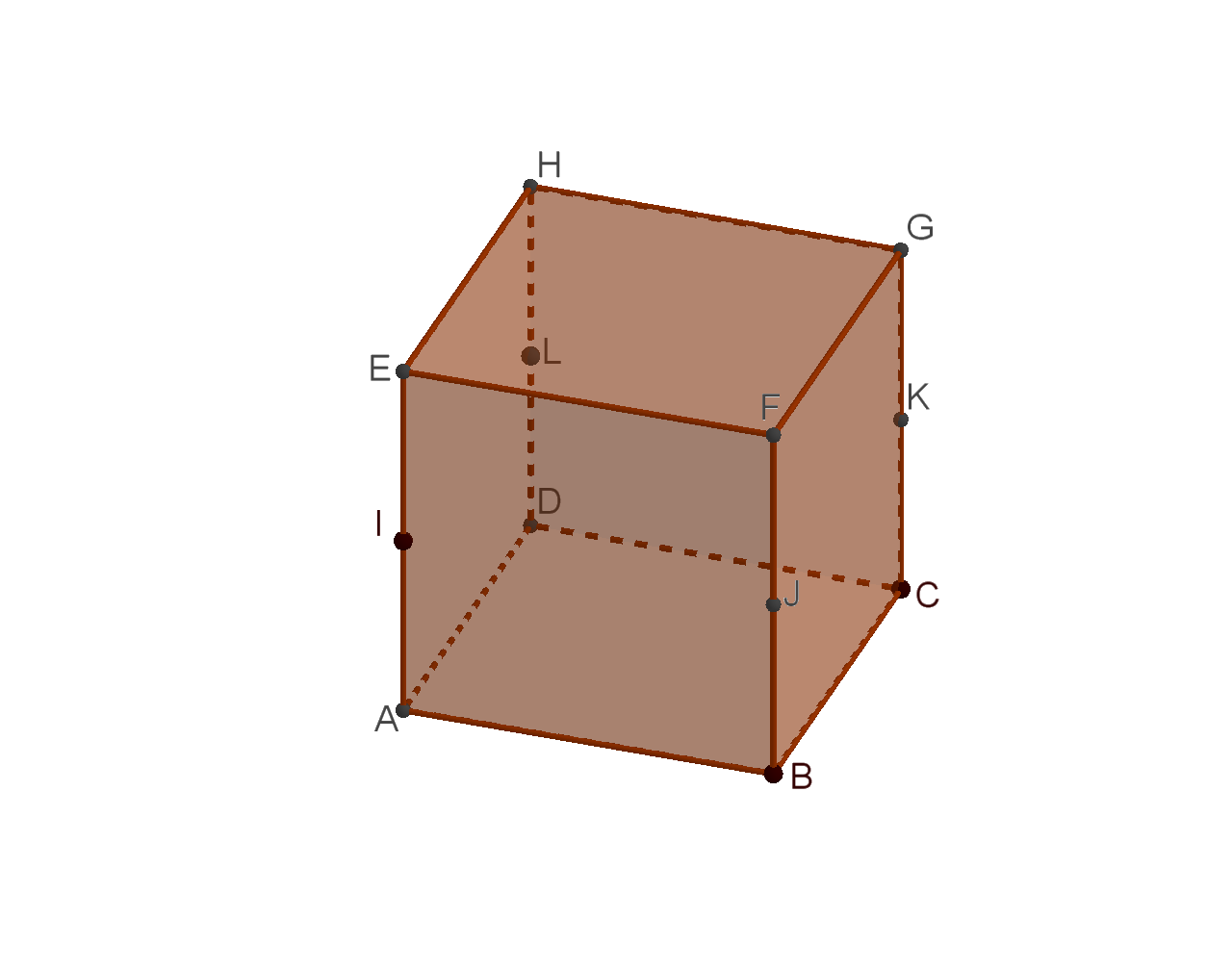
Na kocki s vrhovima istaknute su točke za koje vrijedi
Odgovorite:
Odgovor na svih
pitanja je isti - u paralelnom položaju.
U prošlom zadatku možemo uočiti tzv. tranzitivnost paralelnosti.
Paralelnost pravaca i paralelnost ravnina tranzitivne su relacije. To znači da imaju svojstva:
Ako je i ako je onda je i
Ako je i ako je onda je
Paralelnost je relacija ekvivalencije. To znači da je binarna relacija i da vrijede svojstva refleksivnosti, simetričnosti i tranzitivnosti.
Sva tri svojstva smo već spomenuli. Potražite ih te dokažite da je paralelnost relacija ekvivalencije.
Proučite koje još vrste relacija postoje. Koja je razlika između relacija i funkcija?
Pravac i ravnina u prostoru se mogu sijeći u jednoj točki ili su paralelni. Pritom paralelnost uključuje i slučaj kad pravac leži u ravnini.
Dvije ravnine u prostoru se mogu sijeći po pravcu ili biti paralelne. Pritom paralelnost uključuje slučaj kad se ravnine podudaraju.
Mimoilazni pravci ne pripadaju istoj ravnini.
Četiri različite točke uvijek su komplanarne.
Pravci koji leže u paralelnim ravninama uvijek su paralelni.
Određuju li dva različita paralelna pravca točno jednu ravninu?