

Došli ste na razgovor za posao. Budući poslodavac zadovoljan je razgovorom i posao je vaš. Sada samo trebate dogovoriti svoju plaću. Poslodavac vam daje mogućnost da birate između dvaju modela.
„Što ste odlučili?” pita vas budući šef.
Ako ste bili pozorni u proučavanju eksponencijalnih funkcija, znat ćete odgovor.
Ako niste, pogledajte kako ćete problem riješiti s pomoću Excela.
Ako ste se oduševili i prihvatili drugu ponudu, vrlo ste pogriješili. Na početku se prva ponuda ne čini posebno primamljivom, ali pokušajmo malo računati.
- 1. dan
- 2. dan
- 3. dan
- 4. dan
Ovo baš nije mnogo lipa, zasad nemamo ni jednu kunu. Ni desetog dana stanje ne postaje bolje.
Ali 24. dana imamo plaću veću od one ponuđene za cijeli mjesec.
Kolika je isplata samo zadnjeg dana u mjesecu?
kuna.
Kako prepoznati da je funkcija eksponencijalna, a ne linearna? U sljedećim tablicama prepoznajte i pridružite linearnu funkciju, eksponencijalnu funkciju ili ni jednu ni drugu.
|
|
|||||||||||
|
|
|||||||||||
|
|
Graf koje eksponencijalne funkcije
prolazi točkama
i
U siječnju je prodaja bila kuna. Od siječnja je rasla svaki mjesec. Naka je mjesečna prodaja, a broj mjeseci. Koji eksponencijalni model opisuje situaciju?
Pomoć:
Kolika je prodaja u veljači, ožujku? Podijeli prodaju u veljači s prodajom u siječnju. Koliki je kvocjent?
Vrijednost velike kompanije (u milijunima kuna) procijenjena je eksponencijalnim modelom
Argument
je broj godina s početkom u 2003. godini. Kolika će vrijednost kompanije biti 2018. godine?
U tablici su neke od vrijednosti eksponencijalne funkcije
S pomoću zadanih vrijednosti pronađi funkciju. Nakon toga izračunaj vrijednosti za zadane argumente.

Do sada ste vidjeli kako prepoznati eksponencijalni model, kako ga iz podataka koje imamo pronaći te kako ga primijeniti.
Vrijeme je za malo samostalnog rada.
Pred vama su projektne aktivnosti u dvama različitim projektima. Kroz njih možete proći kako je zapisano, ali možete i modelirati, istraživati, mijenjati. Svoja mala istraživanja provedite u timu, skupini ili samostalno. Surađujte preko Padleta, Yummera i drugih mreža. Izradite prezentacije u PowerPointu ili Preziju. Osmislite scenarij za film i snimite svoje istraživanje. Bez obzira na metodu rada koju odaberete, na kraju svakako rad predstavite razrednim kolegama i nastavniku/nastavnici.
Prirast broja stanovnika
Porast stanovništva i prenapučenost usko su vezani. Postoji opravdani strah od prenapučenosti Zemlje čiji resursi nisu neograničeni. Istražimo kako se kreće i kako će se kretati broj stanovnika Zemlje u drugom desetljeću 21. stoljeća.
Koristeći se internetom, na papiru nacrtajte i popunite tablicu kao u nastavku. Možete se koristiti podatcima sa stranice:
| godina | 2010. | 2011. | 2012. | 2013. | 2014. | 2015. | 2016. | 2017. | 2018. | 2019. | 2020. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| broj stanovnika (u milijunima) |
Odaberite jednu od svjetskih zemalja prema svojemu izboru za koju biste očekivali da će odstupati od modela (epidemije, rat, vremenske nepogode i sl.) te vrijeme promatranja.
Ponovite postupak od a. do e.
Zašto ste očekivali velike razlike?
Jeste li uspjeli pokazati te razlike?
Zakon hlađenja
U prethodnoj ste se jedinici upoznali s Newtonovim zakonom hlađenja. Vrijeme je da provjerimo funkcionira li taj zakon u praksi. Mjerit ćemo, računati, uspoređivati, biti pravi istraživači.
Ponovimo!
Stavimo li tijelo temperature u okolinu temperature nakon vremena temperatura tijela iznosit će:
Pokusom ćemo odrediti konstantu za odabranu tekućinu.
a. Odaberite tekućinu (kava, čaj, voda...).
b. Ugrijte odabranu tekućinu na visoku temperaturu.
c. Posudu odnesite u prostoriju znatno niže temperature.
d. U posudu uronite termometar i svakih sekundi mjerite temperaturu tekućine. Podatke upišite u tablicu kao na slici. Što više podataka prikupite, izračun će biti točniji.
| (min) |
-izmjerena temperatura vode |
-temperatura okoline |
- početna temperatura |
|
|---|---|---|---|---|
e. Podatke u zadnjem stupcu izračunajte.
f. Točke ucrtajte u GeoGebru.
g. Izradite klizač s korakom kako biste bili precizniji (klizač možete lagano pomicati strelicama na tipkovnici).
h. Nacrtajte funkciju
i. Klizačem mijenjajte kako biste „namjestili” funkciju koja će što bolje povezati vaše podatke, tj. točke.
j. Očitajte
k. Ponovite pokus. Uz koji ste odredili izračunajte sada s pomoću zakona hlađenja temperaturu u proizvoljno odabrano vrijeme. Mjerite i usporedite.
Primjer 1.
Pokazat ćemo postupak opisan u prethodnom zadatku.
U tablici su podatci (podatci ne odgovaraju stvarnom mjerenju) i izračun.
(min) -izmjerena
temperatura vode-temperatura
okoline- početna
temperatura
Podatci su u sljedećoj interakciji. Pronađite konstantu.
Upoznali ste se i s Malthusovim modelom rasta populacije. Već smo rekli da taj model nije dobar iz više razloga, a najvažniji je da pretpostavlja kako su stopa rasta i smrtnosti konstantne. Ako je populacija u zatvorenoj sredini, s vremenom stopa rasta počinje padati, a stopa smrtnosti rasti.
Model koji opisuje te promjene je Verhulstov ili logistički model rasta populacije.

Pierre François Verhulst (1804. – 1849.) belgijski je statističar i demograf koji je radio na modelima rasta populacije. Logistički model (sam ga je tako nazvao) predstavio je 1845. bez objašnjenja. Model je ponovno otkriven tek 1920. i od tada se razvija.
Logistička funkcija primjenjuje se u raznim područjima kao što su neuronske mreže, biologija, biomatematika, demografija, ekonomija i medicina.
Vjerojatno je najzanimljivija primjena u lingvistici gdje se prati primjena inovacija u jeziku koja je u početku marginalna, a na kraju zahvaća cijelu populaciju.
Jednostavna logistička funkcija je funkcija oblika
gdje je:
– kapacitet staništa
– početna populacija
– konstanta proporcionalnosti
– vrijeme.
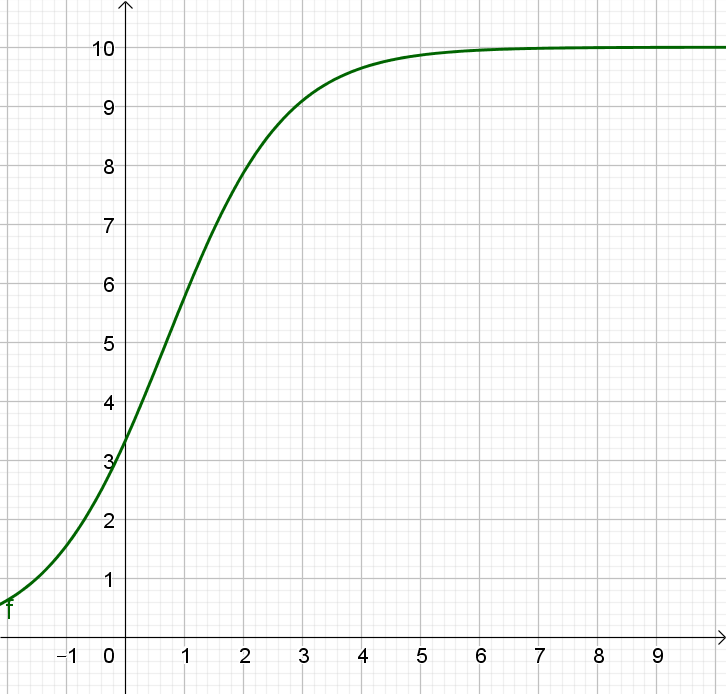
Na slici je logistička funkcija za koju je kapacitet staništa početni broj jedinki a konstanta proprcionalnosti Vidimo da broj jedinki raste eksponencijalno dok populacija ne postigne maksimalan kapacitet, a nakon toga populacija ne raste. To je pojednostavnjeni model.
Logistička funkcija nije uspješna u modelima u kojima je prisutno useljavanje i iseljavanje jedinki populacije. Tada ju je potrebno prilagoditi i model postaje složeniji.
Jedan od primjera modela prirodnog procesa ograničenog rasta su i epidemije zaraznih bolesti.
Broj oboljelih u početku eksponencijalno raste približavajući se najvišoj ili najnižoj vrijednosti, a zatim stagnira.
U slučajevima kada možemo primijeniti Malthusov model riječ je o pandemiji ili epidemiji velikih razmjera.
Svinjska gripa se prvi put pojavila 2. travnja 2009. u Meksiku, u gradiću Veracruzu. Do ranog ožujka zaraženo je bilo stanovništva i gripa se širila dalje. Od zaraženih u Meksiku umrlo ih je a bolest se proširila na države. Postojala je opasnost od pandemije pa je Svjetska zdravstvena organizacija proglasila peti stupanj pripravnosti. Ipak, pokazalo se da se pandemija nije mogla dogoditi.
Provedite istraživanje i utvrdite odgovara li rastu oboljelih više Malthusov ili logistički model.
Podatke o broju oboljelih i umrlih u Meksiku potražite na internetu (možete upotrijebiti i model sa stranice ili stranice). Ako ne uspijete pronaći podatke za Meksiko, odaberite drugu zemlju ili drugu epidemiju.

„Najveći nedostatak ljudske rase je nemogućnost razumjevanja eksponencijalne funkcije.”
Albert Allen Bartlett (1923. – 2013.), profesor fizike na Sveučilištu u Coloradu
Eksponencijalni rast je često podcijenjen. Evo primjera.
Za kraj evo zanimljivog pravila 72.
„To je pravilo brzi složeni kamatni račun koj je primjeren za izračune do prinosa, iznad tog prinosa nastaju veća odstupanja.
Pravilo 72. omogućava brzi izračun:
godina koje su potrebne uz određeni godišnji prinos da se investicija udvostruči
prinos koji je potreban da se, u određenim godinama, investicija udvostruči.
Kako biste dobili broj godina potrebnih da se investicija udvostruči, uz određeni godišnji prinos, podijelite 72 s godišnjim prinosom.
Kako biste izračunali željeni godišnji prinos, podijelite 72 s godinama u kojima želite investiciju udvostručiti.” Izvor
Vrijedi li spomenuto pravilo?
Usporedite pravilo 72. i složeni kamatni račun na primjeru za koji podatke pronađite ili sami zadajte. Koliko je odstupanje?