


Jeste li igrali igru "Pogodi broj koji sam zamislio/la."?
Zamislite broj između
i
Cilj je pogoditi broj sa što manje pitanja. Koliko pitanja trebamo postaviti?
Zamislimo da je broj koji tražimo
Pitanja tad izgledaju ovako:
"Je li broj veći od
"
"Da."
"Je li broj veći od
"
"Da."
"Je li broj veći od
"
"Ne."
Broj je Trebalo je postaviti pitanja.
Zamislimo sada broj između i Koliko pitanja sada treba postaviti? Neka je broj
"Je li broj veći od "
"Da."
"Je li broj veći od "
"Ne."
"Je li broj veći od "
"Ne."
"Je li broj veći od "
"Da."
Broj je Broj postavljenih pitanja je
Svakim pitanjem broj elemenata skupa u kojem je rješenje smanjuje se napola.
Ako je broj između i nakon prvog pitanja broj mogućnosti je Nakon drugog pitanja broj mogućnosti je itd.
Broj minimalnih pitanja rješenje je izraza gdje je broj pitanja. Izraz napišimo s pomoću logaritma.
Ako nemate džepno računalo s logaritmima različitih baza, upotrijebite pravilo za promjenu baze.
Izračunajmo koliko pitanja je potrebno postaviti za pogađanje broja između jedan i milijun.
Zaigrajte igru i provjerite.
Vidjeli smo da se Excelom možemo koristiti u rješavanju problema s eksponencijalnom funkcijom. Možemo li se Excelom koristiti i za logaritamsku funkciju? Možemo.
U sljedećem videu pogledajte kako, te pokušajte i sami.
Vidjeli smo da se s pomoću logaritamske funkcije i primjene pravila računanja mogu riješiti i modelirati neki od problema, da su logaritmi ubrzali procese računanja. U nastavku ćete sami izraditi svoje logaritamsko ravnalo, računati s Napierovim kostima, mjeriti i izraditi logaritamske modele za svakodnevne situacije.
Ali najprije ponovimo i računajmo još malo s logaritmima.
U tablicu postavite vrijednosti funkcije. Baza nije poznata, odredite je iz poznatih argumenata i vrijednosti.
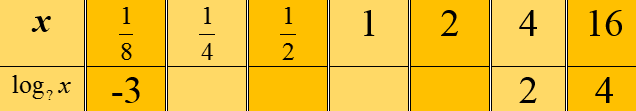
-2
-1
0
1
=
=
Uparite jednake vrijednosti.
|
|
|
|
|
|
|
|
|
Postavite znakove na pravo mjesto.
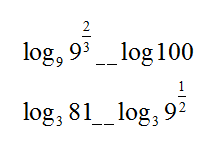
<
>

Kako izračunati magnitudu potresa i koja je veza između magnitude i oslobođene energije, već smo vidjeli. Za određena mjesta na Zemlji imamo formule kojima se može izračunati magnituda potresa. Magnituda ovisi o amplitudi potresa i udaljenosti od epicentra. Za seizmološku postaju Zagreb formula je:
je amplituda potresa, a udaljenost od epicentra.
| Amplituda ( ) | Udaljenost (
) |
Magnituda |
|---|---|---|
Izračunajte magnitudu potresa ako su zadane amplitude i udaljenosti od epicentra. Koristeći u tablici zadane podatke odredi vrijednost nepoznatih podataka računajući u bilježnici (na papir).
Rezultate prikažite u koordinatnom sustavu tako da na os apscisu nanesete amlitudu, a na ordinatu magnitudu koju izračunate. Ponovite postupak na istom grafičkom prikazu za udaljenosti od i
Krivulje nacrtajte različitim bojama.
Uz pomoć GeoGebre pridružite logaritamski model svakoj krivulji. Za koliko se modeli razlikuju?
Istražite može li se logaritamski model primijeniti na rast djece. Za taj projekt bit će vam potrebna pomoć školskog liječnika. Zamolite da vam da podatke o visini djece od do godine života (bez imena naravno). Podaci neka budu za pet djevojčica i pet dječaka za svaku dob. Ako podatke ne uspijete dobiti od liječnika, pronađite ih na internetu.
Izračunajte srednju vrijednost visine za svaku godinu života, za djevojčice i dječake.
Za prikupljanje podatke o srednjoj vrijednosti visina možete koristiti tablicu kao što je ova u nastavku.
| Godine
|
Visina djevojčica ( ) | Godine | Visina dječaci ( ) |
|---|---|---|---|
| ... | ... | ||
Podatke iz tablice prikažite u koordinatnom sustavu.
Nacrtajte u bilježnici na jednom koordinatnom sustavu podatke za djevojčice iz tablice te nacrtajte krivulju. Ponovite postupak za dječake.
Pronađite odgovarajući model rasta za djevojčice i dječake. Provjerite u razredu mjereći visinu koliko je u postotku učenika viših od modela, a koliko nižih.

Često čitamo ljeti kako roditelji ostavljaju djecu u zatvorenim automobilima na suncu na samo nekoliko minuta. Ako se radi o samo nekoliko minuta, zašto o tome pišu novine? Napravit ćete malo istraživanje i utvrditi jesu li napisi u novinama zaista opravdani ili ne.
Za ovaj praktičan rad trebat će vam tremometar i pristup automobilu koji je parkiran na suncu. Odaberite ljetni dan, kad temperatura prelazi Neka odrasla osoba parkira automobil na suncu, a vi postavite termometar u automobil, tako da je na vidljivome mjestu.
Ostanite uz automobil (ali se svakako zaštitite suncobranom i imajte uza se dovoljno tekućine). Nacrtajte na papir tablicu
koja je priložena,
podatke upisujte u tablicu
i bilježite temperaturu svakih
sekundi. Dovoljan broj podataka dobit ćete već nakon sat vremena.
| Vrijeme ( ) | Temperatura ( ) | Vrijeme ( ) | Temperatura ( ) |
|---|---|---|---|
Podatke ucrtajte u koordinatni sustav, tako da na os apscisu nanesete vrijeme, a na os ordinatu temperaturu. Izradite logaritamski model.

Sjećate li se našeg inspektora Bere iz prethodnog modula i slučaja ubojstva na rođendanu?
Inspektor je očitao temperaturu sobe od i izmjerio temperaturu žrtve od
Imao je na raspolaganju Newtonov zakon hlađenja:
Ali nepoznanica, tj. vrijeme, nalazi se u eksponentu. Sad imamo znanje koje nam omogućuje da eksponencijalnu funkciju prevedemo u logaritamsku i riješimo ovaj zločin matematičkim putem. Za početnu temperaturu tijela uzet ćemo
Primjer 1.
Kako smo s aplikacijom koju je Marin izradio uspjeli zaključiti, tako i sada vidimo da se ubojstvo dogodilo sati prije nego što je tijelo pronađeno.

John Napier nije samo tvorac teorije o logaritmima. On je osmislio i mehanizam računanja koji se sastoji od drvene pitagorine tablice, s pomičnim stupcima, koje rabimo kako bi računske operacije množenja, dijeljenja i potenciranja postale brže.
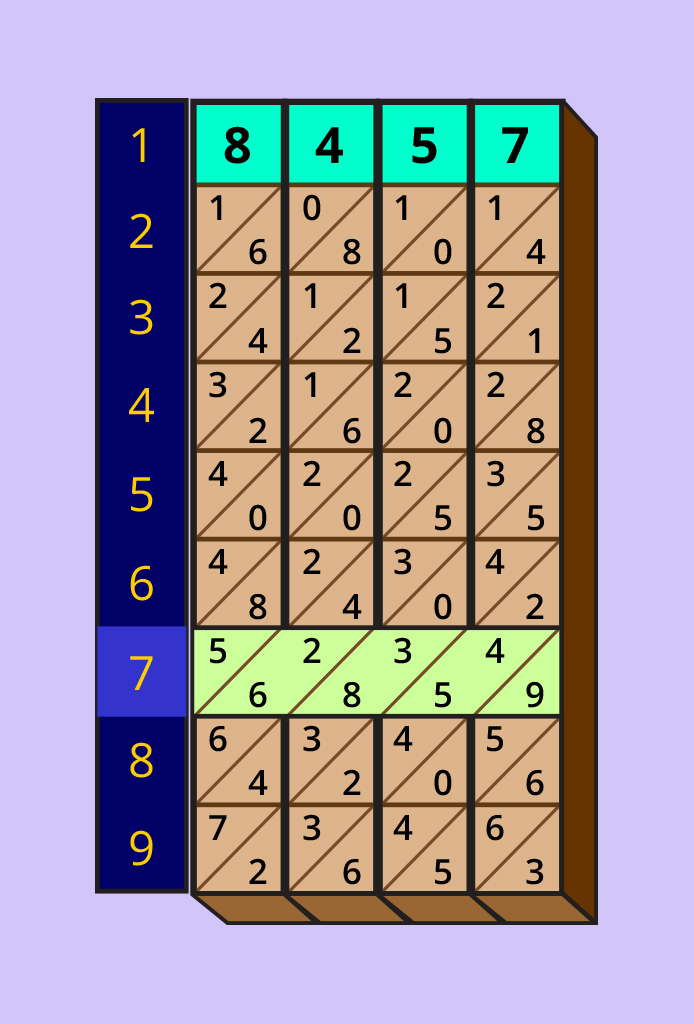
Mehanizam se sastoji od deset stupaca podijeljenih u devet kvadrata. Svaki od stupaca ima u gornjem kvadratu jedan od brojeva iz baze deset, a ispod njime povezanu tablicu množenja. Kvadrati iz tablice su podijeljeni dijagonalom koja dijeli desetice od jedinica, gdje su destice u gornjem trokutu, a jedinice u donjem. Mehanizam je kompletiran baznim stupcem koji se sastoji od brojeva od do
Pomnožimo sada
Spojimo stupce i i slijeva stavimo bazni stupac. U redu (broj kojim množimo) čitamo rezultate zdesna nalijevo zbrajajući brojeve na dijagonalama u tom redu i vodeći računa o prijenosu desetice na sljedeći zbroj.
Dobit ćemo sljedeći rezultat:
(jedini broj dijagonale)
( u dijagonali)
( i dalje, u dijagonali)
( (prijenos) u dijagonali)
(jedini broj iz dijagonale).
Dobiveni broj pišemo obrnutim redoslijedom
Pokušajte množiti i druge brojeve.
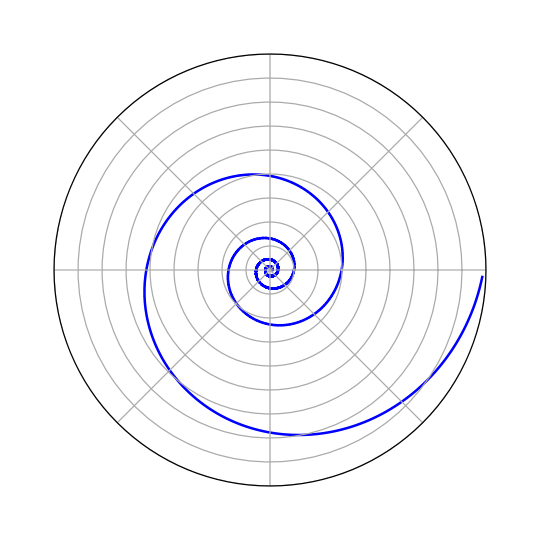
Logaritamska spirala ili spira mirabilis
To je najčešća i najzanimljivija krivulja koja se pojavljuje u prirodnim pojavama, ali i u biljnom i životinjskom svijetu. U nastavku pogledajte galeriju sa slikama logaritamske spirale u prirodi.
Razlikujemo je od Arhimedove spirale po tome da joj razmak između zavoja raste, dok je kod Arhimedove stalan. Bernoulli se toliko divio ovoj spirali da je zatražio da mu bude dio nadgrobnog spomenika. Na žalost majstor koji je radio nadgrobni spomenik nije razlikovao lagaritamsku od Arhimedove spirale, tako da na Bernoullievom nadgrobnom spomeniku imamo Arhimedovu, a ne logaritamsku spiralu.
- jednadžba logaritamske spirale