Matematika 2 - 1.1 Skup kompleksnih brojeva

Na početku...

Na samom početku kompleksni su se brojevi razvijali u svrhu rješavanja matematičkih problema. Danas ih upotrebljavamo u raznim područjima: bežični sustavi, mobilne telefonske mreže, električni krugovi, elektromagnetizam i mnoge druge aplikacije u područjima koja rabe fiziku ili diferencijalne jednadžbe. Fraktali počinju kompleksnim brojevima. Svaki kompleksni broj daje vrijednost pikselu na zaslonu. Veći broj ponavljanja daje veću kvalitetu slike.

Skupovi brojeva

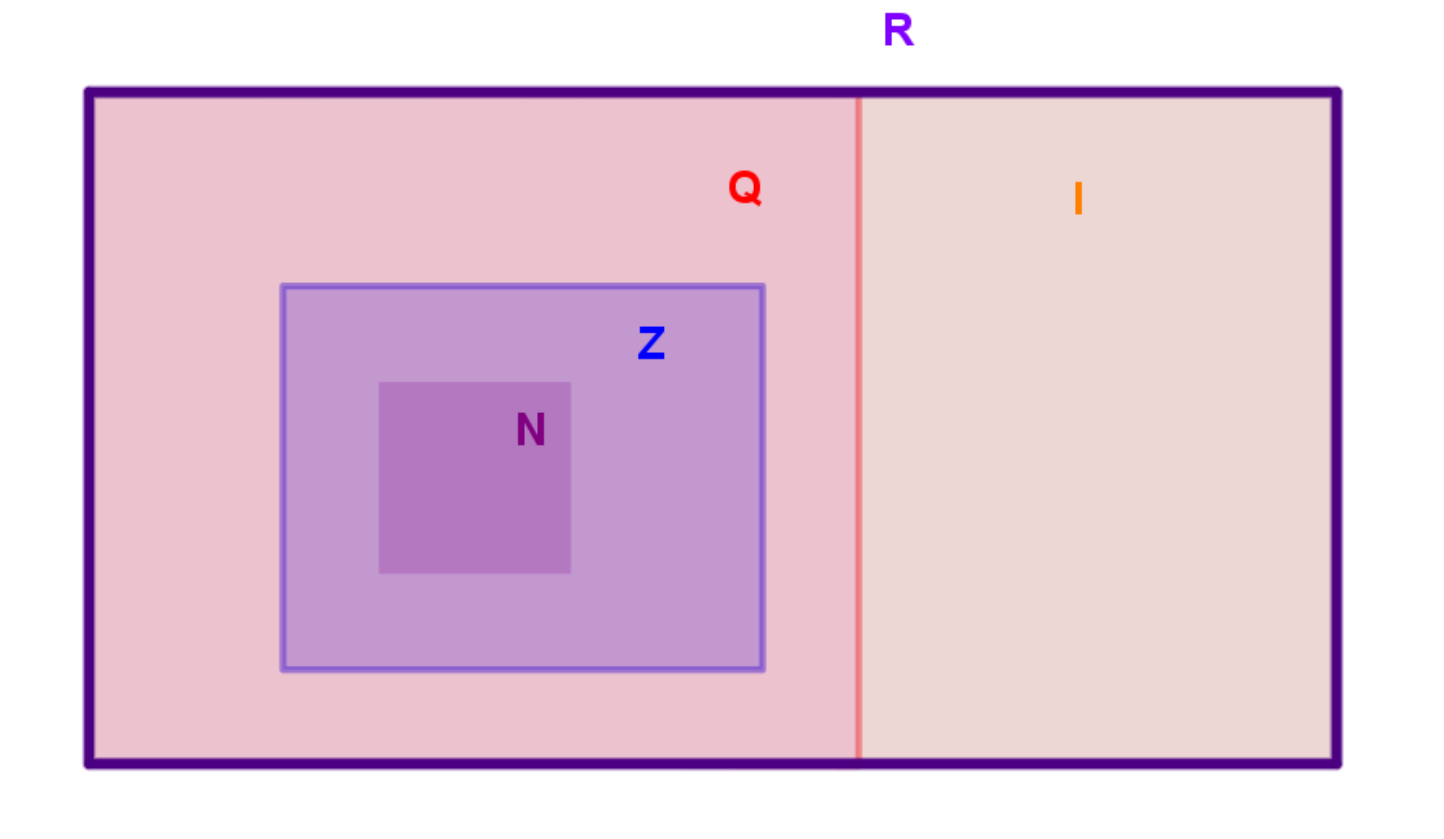
Dosad smo upoznali sljedeće skupove brojeva: skup prirodnih brojeva $N,$ skup cijelih brojeva

Z

, skup racionalnih brojeva

Q

te skup realnih brojeva $R .$

U davna vremena ljudi su se koristili prirodnim brojevima kako bi prebrojili objekte oko sebe. Nakon toga uvedeni su negativni brojevi kojima su se mogle iskazivati, na primjer, negativne vrijednosti temperature. Dijeleći usjeve i posjede ljudi su uvidjeli potrebu za uvođenjem racionalnih brojeva, a iracionalni brojevi pojavili su se pri pokušaju mjerenja dijagonale kvadrata.

Prisjetite se svojstava realnih brojeva. (vidi Matematika 1, Modul Brojevi)

Imaginarna jedinica

Matematičari su se u svojim izračunima susreli s potrebom rješavanja kvadratne jednadžbe $x^{2} + 1 = 0 .$

Navedena jednadžba nema rješenja u skupu realnih brojeva. Zato je uveden novi broj, koji je rješenje te jednadžbe.

Imaginarna jedinica i ima svojstvo da je $i^{2} = - 1 .$

S imaginarnom jedinicom računamo kao i s drugim brojevima.

Pogledajmo kako računamo s imaginarnom jedinicom.

Primjer 1.

Računajmo:

$4 i + 3 i = 7 i$

$- i + 6 i = 5 i$

$i \cdot 0 = 0$

$8 \cdot {(- i)}^{2} = 8 i^{2} = - 8$

$2 + i^{2} = 2 - 1 = 1 .$

Zadatak 1.

Riješite zadatke.

Izračunajte $2 i - 5 i =$

null

null
Izračunajte $3 \cdot 4 i + 7 i =$

null

null
Izračunajte $- 2 i^{2} + i^{2} =$

null

null
Izračunajte $3 i^{2} + 4 =$

null

null

Imaginarni broj

Imaginarni broj je broj oblika $bi,$ gdje je $b$ realni broj, a $i$ imaginarna jedinica.

Primjer 2.

Napišimo nekoliko primjera imaginarnih brojeva.

$- 9 i$

$\sqrt{2} i$

$2.31 i$

Kompleksni broj

Kompleksni broj je broj oblika $a + b i,$ gdje su $a$ i $b$ realni brojevi, a $i$ imaginarna jedinica.

Broj $a$ naziva se realni dio kompleksnog broja, a broj $b$ imaginarni dio kompleksnog broja.

Naputak

Za označavanje kompleksnih brojeva najčešće rabimo oznake $z, w, u, v ...$

Zapis kompleksnog broja $z = a + b i$ nazivamo algebarski zapis kompleksnog broja, gdje su $a$ i $b$ realni brojevi, a $i$ imaginarna jedinica.

Primjer 3.

Odredimo realne i imaginarne dijelove kompleksnih brojeva.

$2 + 9 i$

$\frac{3}{4} - i$

$\sqrt{3}$

$π i$

Broj $2$ je realni, a $9$ imaginarni dio kompleksnog broja.
Broj $\frac{3}{4}$ je realni, a $- 1$ imaginarni dio kompleksnog broja.
Broj $\sqrt{3}$ je realni, a $0$ imaginarni dio kompleksnog broja.
Broj $0$ je realni, a $π$ imaginarni dio kompleksnog broja.

Realni dio kompleksnog broja $z = a + b i$ označavamo s $Re z,$ a imaginarni dio označavamo s $Im z .$ Pišemo $a = Re z,$ $b = Im z .$ Skup kompleksnih brojeva označavamo s $C .$ Primijetimo da je svaki realni broj ujedno i kompleksan broj. Vrijedi, dakle: $R \subset C .$

Zadatak 2.

U tablicu upišite znak + ili -, ovisno o tome kojem skupu brojeva pripada broj iz prvog retka.

Za skupove brojeva možemo promatrati njihovu zatvorenost s obzirom na računske radnje. Kažemo da je skup prirodnih brojeva zatvoren s obzirom na računsku radnju zbrajanja jer je rezultat zbrajanja prirodnih brojeva prirodni broj. Skup prirodnih brojeva nije zatvoren s obzirom na računsku radnju oduzimanja jer rezultat oduzimanja prirodnih brojeva ne mora uvijek biti prirodni broj. Na primjer, $7 - 9 = - 2,$ a $- 2$ nije prirodni broj. Proširenjem skupa prirodnih brojeva na skup cijelih brojeva dobivamo zatvorenost s obzirom na računsku radnju oduzimanja.

Zadatak 3.

Razmislite o zatvorenosti skupova brojeva s obzirom na računske radnje množenja i dijeljenja.

Svi spomenuti skupovi brojeva zatvoreni su s obzirom na računsku radnju množenja. Skupovi prirodnih i cijelih brojeva nisu zatvoreni s obzirom na računsku radnju dijeljenja, ali skup racionalnih brojeva i skup realnih brojeva jest.

Razmislimo, nadalje, o računskim radnjama potenciranja i korjenovanja. Potenciranje možemo svesti na množenje pa zaključujemo da su navedeni skupovi brojeva zatvoreni i s obzirom na potenciranje. U skupu realnih brojeva $\sqrt{- 1}$ nije definiran, pa skup realnih brojeva nije zatvoren s obzirom na računsku radnju korjenovanja.

Funkciju drugog korijena s domenom $R^{+}$ proširujemo na funkciju iste oznake i naziva, ali s domenom $R .$ Pri korjenovanju služimo se pravilom $\sqrt{- x} = i \sqrt{x}, x > 0$ zato što navedeni broj kvadriran daje $- x .$

Npr.

$\sqrt{- 16} = 4 i,$ a ne $\sqrt{- 16} = \pm 4 i .$

Kao što je i $\sqrt{9}$ jednak $3,$ a ne $\pm 3 .$

Jednakost kompleksnih brojeva

Brojeve u skupu realnih brojeva možemo uspoređivati. Pogledajmo možemo li to učiniti u skupu kompleksnih brojeva.

Dva su kompleksna broja jednaka ako su im jednaki realni dijelovi i ako su im jednaki imaginarni dijelovi. Vrijedi i obratno.

Pišemo:

$\begin{array}{l} a + b i = c + d i \Leftrightarrow a = c, b = d \end{array}$

Primjer 4.

Usporedimo kompleksne brojeve.

$z_{1} = \frac{1}{2} + \frac{1}{4} i,$ $z_{2} = 0.5 + 0.25 i$

$z_{1} = 0.4 + 0.3 i,$ $z_{2} = 0.3 + 0.4 i$

$z_{1} = - 7 + i,$ $z_{2} = 7 + i$

$z_{1} = 2 + 3 i,$ $z_{2} = 2 + 4 i$

$Re z_{1} = \frac{1}{2} = 0.5 = Re z_{2}$

$Im z_{1} = \frac{1}{4} = 0.25 = Im z_{2}$

Brojevi $z_{1}$ i $z_{2}$ su jednaki jer su međusobno jednaki njihovi realni te njihovi imaginarni dijelovi.
$Re z_{1} = - 7 \neq 7 = Re z_{2}$

$Im z_{1} = 0.3 \neq 0.4 = Im z_{2}$

Brojevi $z_{1}$ i $z_{2}$ nisu jednaki jer nisu međusobno jednaki njihovi realni, a ni imaginarni dijelovi.
$Re z_{1} = - 7 \neq 7 = Re z_{2}$

$Im z_{1} = 1 = 1 = Im z_{2}$

Brojevi $z_{1}$ i $z_{2}$ nisu jednaki jer nisu međusobno jednaki njihovi realni dijelovi.
$Re z_{1} = 2 = 2 = Re z_{2}$

$Im z_{1} = 3 \neq 4 = Im z_{2}$

Brojevi $z_{1}$ i $z_{2}$ nisu jednaki jer nisu međusobno jednaki njihovi imaginarni dijelovi.

Primjer 5.

Za koje realne brojeve $x$ i $y$ vrijede jednakosti:

$5 + (2 - x) i = y - 3i$

$2 (x - 1) - (y + 3) i = 4 + 3i ?$

Prema definiciji jednakosti kompleksnih brojeva uspoređujemo realne i imaginarne dijelove kompleksnih brojeva na objema stranama jednakosti. Zapisujemo $5 = y$ i $2 - x = - 3 .$

Nakon rješavanja dobivenih jednadžbi slijedi: $y = 5$ i $x = 5 .$
Na isti način dobivamo jednadžbe $2 (x - 1) = 4$ te $- (y + 3) = 3 .$

Rješenja tih jednadžbi su $x = 3$ i $y = - 6 .$

U skupu kompleksnih brojeva ne postoje tvrdnje kao kompleksni broj je manji od $0,$ pozitivni kompleksni broj i slično.

Kolekcija zadataka 1

Zadatak 4.

Riješite zadatke.

Izračunajte.
$4 i + \sqrt{- 16} =$
Dopunite rečenicu.
U kompleksnom broju $z = - 3 + 4 i,$ broj $-3$ nazivamo dio broja $z,$ broj $4$ nazivamo dio broja $z .$
Odredite realne dijelove brojeva.
$Re (13 - 9 i)$ ,
$Re (5)$ ,
$Re (- 17 i)$ ,
$Re (4 - i^{2})$ .

null

Zadatak 5.

Koje su od sljedećih jedanosti točne:

$2.3 - 4 i = \frac{23}{10} - \frac{24}{6} i$

Da

Ne

null

null
$\frac{\sqrt{3}}{3} - \frac{1}{\sqrt{3}} + i^{2} = - 1$

Da

Ne

null

null
${(1 - i)}^{2} = - 2 i$

Da

Ne

null

null
Izračunajte vrijednosti realnih brojeva $x$ i $y$ tako da jednakosti budu istinite.
$5 \cdot (3 - x) - y \cdot (1 + i) = 2 + 5 i$
$x =$
$y =$

null

null
Za razlomak upotrijebite kosu crtu /.
$\begin{array}{l} \begin{array}{l} (1 - i) \cdot (x + y) + (2 + 3 i) \cdot (x - y) = 1 \end{array} \end{array}$
$x =$
$y =$

null

null

Zatvori

...i na kraju

Kompleksni brojevi su matematičarima dugi niz godina stvarali dvojbe. Smatrali su ih nemogućima. Zbog toga su ih nazivali zamišljenim brojevima. Prema latinskoj riječi imaginare dobili smo naziv imaginarni brojevi. Njihovu primjenu u svakodnevnom životu nije jednostavno potpuno objasniti u srednjoškolskoj matematici.

1.1 Skup kompleksnih brojeva