Matematika 2 - 6.4 Računanje s logaritmima

Na početku...

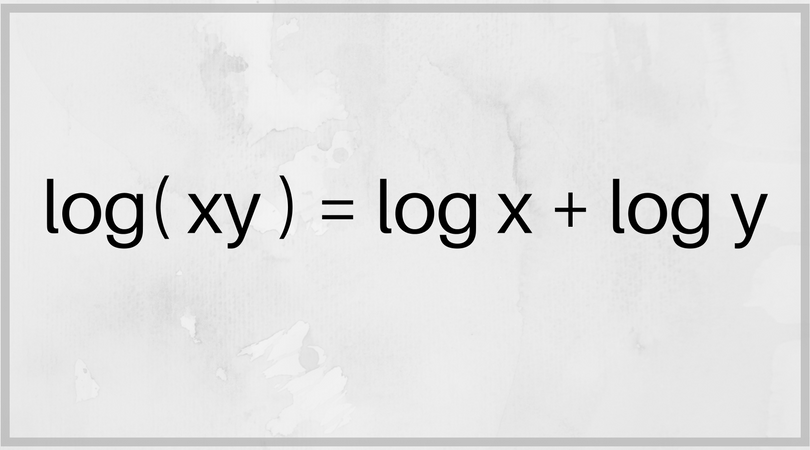
Prema pisanju matematičara i pisca Iana Stewarta u knjizi "U potrazi za nepoznatim: $17$ jednadžbi koje su promijenile svijet", među tih $17$ veličanstvenih nalazi se i jednadžba:

Što je razlog toj izjavi? Kako je jedna jednadžba mogla promijeniti svijet?

Ako bolje pogledate, na jednoj strani je množenje, a na drugoj zbrajanje. S pomoću te jednadžbe množenje se svodi na zbrajanje. Do razvoja računala to je bio jedan od uobičajenih načina množenja velikih brojeva.

Primjena je ubrzala izračune u astronomiji, fizici i inženjeringu.

William Oughtred - izumitelj logaritamskog računala — William Oughtred

Tko je i kada izumio prvo pomagalo za računanje? Govorimo o prvom "kalkulatoru".

Nakon što je John Napier objavio koncept o logaritmima, Edmund Gunter (matematičar, geometar, svećenik i astronom) razmišlja o mehaničkom pomagalu za računanje. Oko 1620. on izrađuje Gunterovu ljestvicu, na kojoj se s pomoću šestara moglo množiti i dijeliti. Iz te sprave kasnije se razvilo logaritamsko računalo.

1632. William Oughtred konstruirao je prvo logaritamsko računalo, zapravo dvije vrste: linijsko i kružno. Opisao ih je u knjizi "Krugovi proporcija i vodoravna sprava".

Svojstva logaritamske funkcije

Svojstva koja ćemo navesti posljedica su svojstava eksponencijalne funkcije koja ste već istraživali. Za početak imamo dva jednostavna pravila koja proizlaze iz veze eksponencijalne i logaritamske funkcije, a koja ste već spominjali.

$(1) \log_{a} a = 1$ zato što je $a^{1} = a$

$(2) \log_{a} 1 = 0$ zato što je $a^{0} = 1$

Tim svojstvima često ćemo se koristiti u idućim primjerima i zadacima, kao i jednostavnijim izračunima vrijednosti logaritamske funkcije preko definicije.

Često se koristimo:

$\ln e = 1$

$\log 10 = 1$

Logaritam umnoška

Prvo svojstvo ili pravilo je ono koje smo naveli u uvodu, pravilo umnoška, koje je posljedica pravila $a^{m} \cdot a^{n} = a^{m + n} .$

Za bilo koja dva pozitivna broja $m$ i $n$ i bazu $a$ vrijedi pravilo:

$(3) \log_{a} (m \cdot n) = \log_{a} m + \log_{a} n$

Logaritam umnoška jednak je zbroju logaritama faktora.

Dokažimo ovo pravilo.

$\log_{a} m = X \Rightarrow m = a^{X}$

$\log_{a} n = Y \Rightarrow n = a^{Y}$

Sada imamo:

$m \cdot n = a^{X} \cdot a^{Y} = a^{X + Y} \Rightarrow \log_{a} (m \cdot n) = X + Y = \log_{a} m + \log_{a} n$

Primjer 1.

Izraz $\log_{2} (32)$ izrazimo kao sumu logaritama.

$\log_{2} (32) = \log_{2} (2 \cdot 16) = \log_{2} 2 + \log_{2} 16 = 1 + 4 = 5$

Izraz $\log_{a} p^{3} + \log_{a} q$ napišimo kao jedan logaritam.

$\log_{a} p^{3} + \log_{a} q = \log_{a} (p^{3} \cdot q)$

Zadatak 1.

Izraze prikažite kao zbroj logaritama.

$\log_{5} (5 \cdot 25)$
$\log (0.2 \cdot x)$
$\ln (2 e)$

$\log_{5} (5 \cdot 25) = \log_{5} 5 + \log_{5} 25 = 1 + 2 = 3$
$\log (0.2 \cdot x) = \log \frac{2}{10} + \log x = \log \frac{1}{5} + \log x$
$\ln (2 e) = \ln 2 + \ln e = \ln 2 + 1$

Logaritam potencije

Za svaki pozitivni broj $m,$ bazu logaritma $a,$ i svaki relani broj $p$ vrijedi pravilo:

$(4) \log_{a} m^{p} = p \cdot \log_{a} m$

Logaritam potencije s bazom $m$ i eksponentom $p$ jednak je umnošku eksponenta $p$ i logaritma od $m .$

Dokažimo!

Neka je $X = \log_{a} m .$

$X = \log_{a} m \Rightarrow a^{X} = m$

Potencirajmo obje strane eksponentom $p .$

${(a^{X})}^{p} = m^{p} \Rightarrow a^{X p} = m^{p}$

Prikažimo sada kao logaritam.

$\log_{a} m^{p} = X p,$ što uz $X = \log_{a} m$ daje:

$\log_{a} m^{p} = (\log_{a} m) \cdot p = p \cdot \log_{a} m$

Primjer 2.

Na izraze primijenimo pravilo logaritma potencije.

$\log_{11} 11^{- 3}$

$\log_{7} \sqrt[4]{49}$

$\ln x^{5}$

Rješenje:

$\log_{11} 11^{- 3} = - 3 \cdot \log_{11} 11 = - 3$

$\log_{7} \sqrt[4]{49} = \frac{1}{4} \log_{7} 49 = \frac{1}{4} \cdot 2 = \frac{1}{2}$

$\ln x^{5} = 5 \cdot \ln x$

Zadatak 2.

Izraze napišite kao umnožak.

$\log_{a} y^{5}$
$\log 100^{3}$
$\ln \sqrt[3]{e}$

$\log_{a} y^{5} = 5 \log_{a} y$
$\log 100^{3} = 3 \log 100 = 3 \cdot 2 = 6$
$\ln \sqrt[3]{e} = \ln e^{\frac{1}{3}} = \frac{1}{3} \ln e = \frac{1}{3}$

Logaritam kvocijenta

Za svaki pozitivan broj $m$ i $n$ i svaku bazu logaritma $a$ vrijedi:

$(5) \log_{a} \frac{m}{n} = \log_{a} m - \log_{a} n$

Logaritam kvocijenta jednak je razlici logaritama djeljenika i djelitelja.

Dokaz tog pravila izvest ćemo koristeći se pravilom za logaritam produkta i potencije.

$\log_{a} \frac{m}{n} =$ $\log_{a} (m \cdot n^{- 1}) = \log_{a} m + \log_{a} n^{- 1} = \log_{a} m + (- 1) \cdot \log_{a} n = \log_{a} m - \log_{a} n$

Primjer 3.

Prikažimo kao razliku logaritama izraz $\log_{2} \frac{4}{b}$

$\log_{2} (\frac{4}{b}) = \log_{2} 4 - \log_{2} b = 2 - \log_{2} b$

Izraz prikažimo kao jedan logaritam.

$\log_{b} 64 - \log_{b} 16 = \log_{b} (\frac{64}{16}) = \log_{b} 4$

Zadatak 3.

Primijenite pravilo za logaritam kvocijenta u sljedećim zadacima.

Prikažite kao razliku logaritama

$\log_{b} \frac{75}{4}$
Prikažite kao jedan logaritam i pojednostavnite.

$\log 0.01 - \log 100$

$\log_{b} \frac{75}{4} = \log_{b} 75 - \log_{b} 4$
$\log 0.01 - \log 100 = \log (\frac{0.01}{100}) = \log (\frac{\frac{1}{100}}{100}) = \log (\frac{1}{10000}) = \log 10 000^{- 1} = - 1 \log 10 000 = - 4$

Primijenite pravila za računanje s logaritmima i spojite izraze.

$\log_{a} m - \log_{a} n$	$\log_{a} \frac{m}{n}$
$\log_{a} m + \log_{a} n$	$\log_{a} m^{p}$
$p \log_{a} m$	$\log_{a} (m \cdot n)$

null

Primjena pravila

Primjer 4.

Izraz $\log_{a} \frac{b y^{3}}{x^{2} y^{4}}$ napišimo u obliku sume ili razlike logaritama.

$\log_{a} \frac{b y^{3}}{x^{2} y^{4}} = \log_{a} (b y^{3}) - \log_{a} (x^{2} y^{4})$ pravilo za logaritam kvocijenta

$\log_{a} \frac{b y^{3}}{x^{2} y^{4}} = \log_{a} b + \log_{a} y^{3} - (\log_{a} x^{2} + \log_{a} y^{4})$ pravilo za logaritam umnoška

$\log_{a} \frac{b y^{3}}{x^{2} y^{4}} = \log_{a} b - \log_{a} y - 2 \log_{a} x$ pravilo za logaritam potencije

Pojednostavnimo izraz.

$5 \log_{a} x - \log_{a} b + \frac{1}{3} \log_{a} y$

$5 \log_{a} x - \log_{a} b + \frac{1}{3} \log_{a} y = \log_{a} x^{5} - \log_{a} b + \log_{a} \sqrt[3]{y}$ pravilo za logaritam potencije

$5 \log_{a} x - \log_{a} b + \frac{1}{3} \log_{a} y = \log_{a} \frac{x^{5}}{b} + \log_{a} \sqrt[3]{y}$ pravilo za logaritam kvocijenta

$5 \log_{a} x - \log_{a} b + \frac{1}{3} \log_{a} y = \log_{a} (\frac{x^{5} \sqrt[3]{y}}{b})$ pravilo za logaritam umnoška

Primjer 5.

Ako je zadano $\log_{b} 2 \approx 0.301$ i $\log_{b} 3 \approx 0.477,$ izračunajte vrijednost izraza

$\log_{b} 6$

$\log_{b} \frac{2}{3}$

Riješenje:

$\log_{b} 6 = \log_{b} (2 \cdot 3) = \log_{b} 2 + \log_{b} 3 = 0.301 + 0.477 \approx 0.778$

$\log_{b} \frac{2}{3} = \log_{b} 2 - \log_{b} 3 = 0.301 - 0.477 \approx - 0.176$

Zadatak 4.

Primijenite pravila za računanje s logaritmima i napišite kao sumu ili razliku logaritama.
- $\ln \frac{3}{2 x^{5}}$
- $\log \sqrt{\frac{x^{6}}{p^{5} q}}$
- $\log_{c} \sqrt[3]{\frac{x y z^{5}}{a^{2} b^{4}}}$
Primijenite pravila za računanje s logaritmima i napišite kao jedan logaritam.
- $\log_{n} 10 000 - \log_{n} 100$
- $\ln 27 - \ln 9$
- $\frac{1}{2} \log_{x} a - \log_{x} 2$
Ako je zadano $\log_{a} 3 \approx 1.099$ i $\log_{a} 5 \approx 1.609,$ izračunajte vrijednost izraza.
- $\log_{a} \frac{5}{3}$
- $\log_{a} \frac{3}{a}$
- $\log_{a} (15 a)$

1. $\ln 3 - \ln 2 - 5 \ln x$
2. $3 \log x - \frac{5}{2} \log p - \frac{1}{2} l o g q$
3. $\frac{1}{3} \log_{c} x + \frac{1}{3} \log_{c} y + \frac{5}{3} \log_{c} z - \frac{2}{3} \log_{c} a - \frac{4}{3} \log_{c} b$
1. $\log_{n} 100$
2. $\ln 3$
3. $\log \frac{\sqrt{a}}{2}$
1. $0.510$
2. $0.099$
3. $3.708$

Izrazi $a^{\log_{a} x}$ i $\log_{a} a^{x}$

U prethodnim jedinicama kroz kompoziciju funkcija već ste vidjeli čemu su ova dva izraza jednaka. Dokažimo sada algebarski.

Ako je $y = \log_{a} x,$ slijedi da je $a^{y} = x .$ Sad prvi izraz uvrstimo u drugi.

$a^{\log_{a} x} = x$ $(6)$

Drugo pravilo posljedica je logaritma produkta.

$\log_{a} a^{x} = x \log_{a} a = x \cdot 1 = x$ $(7)$

Primjer 6.

Pojednostavnimo sljedeće izraze.

$\log_{b} b^{4}$

Primijetimo da ovdje izraz možemo pojednostavniti direktno primjenom pravila $(6)$ ili koristeći se logaritmom potencije i $\log_{b} b = 1 .$

U oba slučaja rješenje je jednako $4 .$

Sad već znate nekoliko postupaka koje možete primijeniti kod rješavanja zadataka. Većina zadataka može se riješiti na barem dva načina. Na vama je da izaberete brži ili zanimljiviji, ovisno o situaciji.

$\ln e^{- 2} = - 2$

$\log 10^{- 3} = - 3$

Primjer 7.

Pojednostavnimo sljedeće izraze.

$2^{\log_{2} \frac{3}{5}} = \frac{3}{5}$

$e^{\ln (7)} = 7$

$10^{\log 5} = 5$

Zadatak 5.

Pojednostavnite izraze koristeći se pravilima $(6)$ i $(7) .$

$\log_{c} c^{5}$
$\ln e^{(x - 3)}$
$5^{\log_{5} (3 - y)}$
$e^{\ln {(x - 2)}^{2}}$

$5$
$x - 3$
$3 - y$
${(x - 2)}^{2}$

...i na kraju

Kreativnost ne znači samo proučavanje jednog područja u detalje. Kreativnost je povezivanje različitih područja.

Da bi se brže računalo matematičari su tražili alat. Pogledajte zašto je to trebalo pomorcima i kako su matematičari, astronomi i izumitelji instrumenata pomogli da plovidba bude sigurnija.

6.4 Računanje s logaritmima