Obla geometrijska tijela su tijela omeđena barem jednom zakrivljenom plohom. Postoje i uglata geometrijska tijela, koja su omeđena mnogokutima.
Uglata geometrijska tijela nastaju kao presjeci poluprostora danih ravnina. Kako nastaju obla geometrijska tijela?
Razlikujete li ih? Znadete li s koliko je ploha omeđeno svako geometrijsko tijelo?
Razvrstajte dana geometrijska tijela u dvije skupine.
S koliko su ploha omeđena dana geometrijska tijela?
| Tetraedar | |
| Valjak | |
| Šesterostrana piramida | |
| Stožac | |
| Kvadar | |
| Kugla | |
| Trostrana krnja piramida |
Pogledajte sljedeću animaciju. Uočite koja ravninska krivulja rotira, oko čega rotira i što nastaje tom rotacijom.
Zaključimo!
Oko promjera rotira
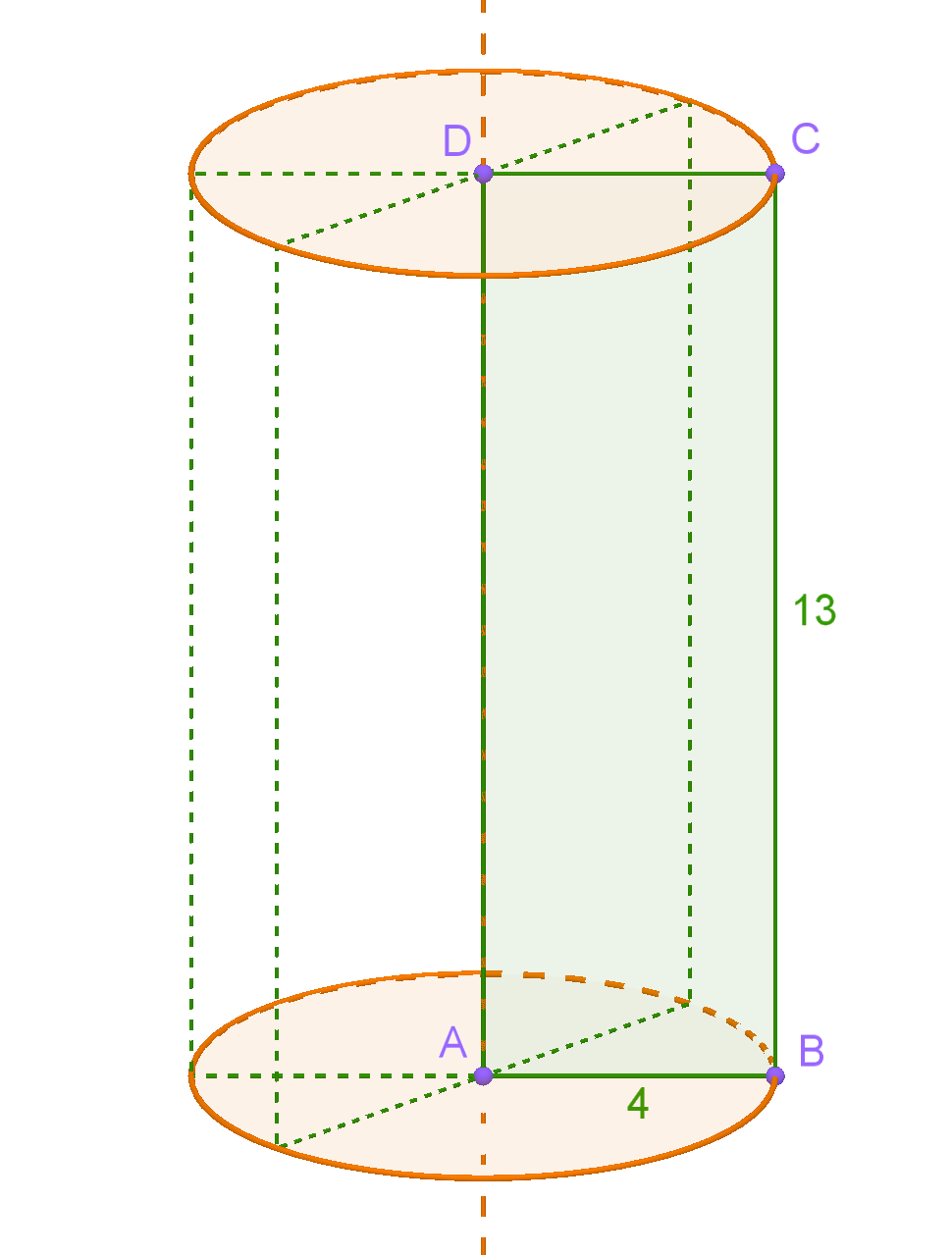
Pravokutnik dužine i širine rotira oko svoje dulje stranice. Izračunajte oplošje i obujam nastaloga geometrijskog tijela.
Pogledajmo još jedanput što nastaje rotacijom pravokutnika Uočite na slici što su stranice pravokutnika u novonastalom valjku pa riješite zadatak.
i
i

Izračunjate oplošje i obujam geometrijskog tijela nastalog rotacijom pravilnog šesterokuta oko njegove stranice
Na slici možete vidjeti rotacijsko tijelo nastalo tom rotacijom napravljeno u GeoGebri.
U sljedećoj interakciji istražite novonastalo geometrijsko tijelo. Možete rotirati šesterokut zadanim klizačem te prikazati ili skriti neke dijelove od kojih se sastoji rotacijsko tijelo. Nakon istraživanja, riješite zadatak. Kao pomoć, u interakciji su dane neke veličine. Usporedite ih sa svojim rješenjem.
Os rotacije ne mora biti stranica geometrijskog lika koji rotira.
Jednakokračni pravokutni trokut rotira oko pravca usporednog s jednom katetom duljine i udaljenog od katete za Izračunajte oplošje i obujam nastaloga rotacijskog tijela.
Uočimo dva geometrijska tijela visine krnji stožac polumjera i te valjak polumjera
Obujam rotacijskog tijela jednak je razlici obujma krnjeg stošca i valjka. Dobiveno rotacijsko tijelo omeđeno je plaštom krnjeg stošca, plaštem valjka te kružnim vijencem.

Pappus-Guldinova pravila
Guldinova pravila ili Pappusova pravila olakšavaju nam računanje oplošja i obujma nekih tijela nastalih rotacijom. Primjenjuju se pri rotacijama u kojima je cijela ravninska krivulja koju rotiramo s iste strane osi rotacije (ne sijeku se). Os rotacije i krivulja u istoj su ravnini.
Dva su Guldinova pravila, za oplošje i obujam nastaloga rotacijskog tijela. Za račun su potrebne duljina krivulje te udaljenost težišta krivulje od osi rotacije.
Klasični primjer je računanje oplošja i obujma torusa.
Torus je geometrijsko tijelo dobiveno rotacijom kružnice oko osi koja leži u ravnini kružnice i ne siječe je.
Neka je dana kružnica polumjera
čije je središte od osi rotacije udaljeno za
Izračunajte oplošje i obujam dobivenog torusa.
Koje geometrijsko tijelo nastaje rotacijom danog lika oko istaknute osi rotacije?
Podijelite se u razredu u pet skupina i rotacijskim tijelima iz 5. zadatka odredite oplošje i obujam. Je li zadano dovoljno podataka za određivanje nepoznatih elemenata rotacijskih tijela?
Oblikujte zadane likove iz kartona ili nekoga drugoga čvrstog materijala te napravite simulaciju nastalog rotacijskog tijela.
Nedostaje jedan podatak. Neka je treći vrh koji ne leži na osi rotacije od nje udaljen jed.
U valjak je upisana pravilna šesterostrana prizma. Odredite omjer površine plašta valjka i prizme.
Na baze jednakostraničnog valjka postavljene su dvije polukugle. Koliko je oplošje toga tijela ako mu je obujam
Oko dvije kugle koje se dodiruju izvana opisan je stožac. Obujam jedne kugle osam je puta veći od druge, a polumjer manje kugle iznosi
Izračunajte površinu plašta i obujam stošca. Skicirajte!
Dakako, do sada spominjana geometrijska tijela nisu jedina tijela koja postoje.
Istražite gdje se koriste bačve (posude za tekućine), a gdje možemo susresti obelisk (egipatski obelisk, mezopotamska umjetnost, u graditeljstvu kao ukrasni dio).