Matematika 2 - Aktivnosti za samostalno učenje

Na početku...

Kako biste uspješno rješavali probleme koji su za vas pripremljeni, provjerite znate li odgovore na sljedeća pitanja:

Što znači eksponencijalni rast, a što pad?
Zašto su logaritmi važni?
Kako se koristimo logaritmima da bismo riješili jednadžbu?
Koje se situacije mogu predočiti eksponencijalnom, a koje logaritamskom funkcijom?
Koje su primjene logaritamskih jednadžbi i nejednadžbi?
Zašto broj $e ?$ Kako zovemo logaritam s bazom $e ?$

Broj $e$ nalazi se i u arhitekturi.

U St. Luisu nalazi se Gateway Arch, veliki luk izgrađen uz zapadnu obalu rijeke Mississippi, u državi Missouri. Luk je izgrađen od nehrđajućeg čelika, širine $192 m$ i visine $192 m$ te postavljen na obalama iznad rijeke. Dizajnirao ga je Eero Saarinen i građen je u razdoblju od 1963.-1965.

Ono što je nama zanimljivo jest to da se luk može opisati jednadžbom $y = a (e^{b x} + e^{- b x}) .$

U nastavku pogledajte kako se možete uvjeriti da je to zaista tako. Pokušajte i sami s nekim drugim građevinama ili prirodnim fenomenima.

Zadatak 1.

Ponovimo još jedanput rješavanje logaritamskih i eksponencijalnih jednadžbi i nejednadžbi.

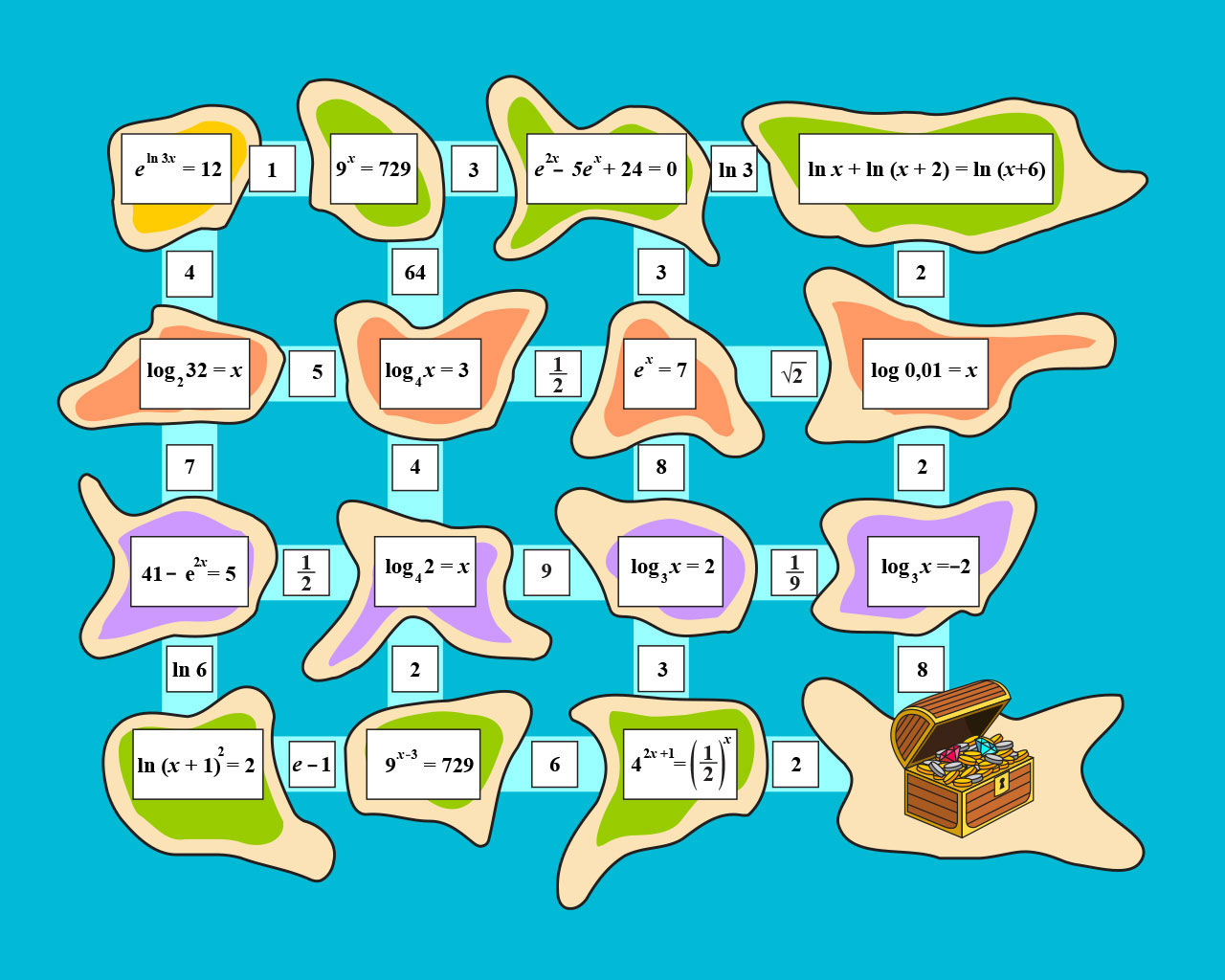
Gusari su ostavili neobičnu kartu s blagom. Na karti su otoci i na svakom otoku je po jedna jednadžba. Sa svakog otoka vode dva ili tri smjera do idućeg. Na svakom smjeru je broj. Samo je jedan broj rješenje jednadžbe s otoka. Riješi jednadžbu i otkrit ćeš kojim putem trebaš nastaviti potragu, tj. koji je otok sljedeći. Na kraju puta čeka te škrinja s blagom.

Poredaj ponuđena rješenja tako da, krenuvši sa žutog otoka, stigneš do škrinje s blagom.

$3$
$\frac{1}{9}$
$5$
$\frac{1}{2}$
$4$
$\ln 6$
$2$
$e - 1$
$6$
$9$
$- \frac{2}{5}$
$\ln 3$
$- 2$
$64$

null

Koliko pozitivnih cijelih brojeva manjih od

$1000$ zadovoljava nejednadžbu

$x^{3 x + 1} > x^{x + 139} ?$ .

null

Ako je $3^{y} \geq 4^{x} - 2,$ koliko iznosi vrijednost nepoznanica?

$x = 2, y = 2$

$x = 3, x = 3$

$x = 2, y = 3$

null

Što je manje: $71^{70}$ ili $70^{71} ?$

$71^{70}$

$70^{71}$

null

Ako znamo da je $\ln 3 < \ln 5,$ što je manje: $\ln {(\ln (\ln 5))}^{2}$ ili ${(\ln (\ln 3))}^{2} ?$

$\ln {(\ln (\ln 5))}^{2}$

${(\ln (\ln 3))}^{2}$

null

Koliko pozitivnih cijelih brojeva zadovoljava nejednadžbu

$\log_{4} x^{2} + \log_{x} 16 - 5 < 0 ?$

null

Je li točna nejednakost $\log_{9} 71 < \log_{8} 61 ?$

null

Samostalne aktivnosti-istražimo!

Praktična vježba

Istražimo još jedanput eksponencijalni rast i primijenimo eksponencijalnu jednadžbu.

Materijal koji nam je potreban jest veći komad papira pravokutnog oblika.

Presavinimo papir napola. Sada imamo dva komada papira čija površina je pola površine početnog komada papira.
Presavinimo papir ponovno. Koliko dijelova sada imamo? Kolika je površina svakog dijela u odnosu na početnu površinu?
Nastavite presavijati papir sve do trenutka kad ga više ne možete presavinuti.
Zapišite funkciju koja opisuje broj dijelova papira nastalih nakon $x$ presavijanja.
Ako smo papir presavinuli $20$ puta, koliko imamo novih komada papira?
Možete li pronaći vezu između broja presavijanja i površine novih dijelova?
Kolika je površina papira koji smo presavinuli $20$ puta?

Izmjerite površinu početnog komada papira. Nakon presavijanja, do trenutka kada to više ne možete učiniti, izmjerite duljine stranica i izračunajte površinu novog komada papira.

Kolika je najmanja površina koju možemo dobiti? Postavite nejednadžbu nakon što više ne budete mogli presavijati papir.

Uz pomoć formule koju ste dobili u f) zadatku izračunajte broj presavijanja.

Funkcija koja opisuje broj dijelova nakon x presavijanja je $f (x) = 2^{x}$

Funkcija koja opisuje ovisnost površine nakon x presavijanja je $f (x) = {(\frac{1}{2})}^{x} .$

Kolekcija zadataka 1

Zadatak 2.

Na novom planetu Logaritmiji 2016. otkrivena je nova živa vrsta. Jedino što znamo o njoj je da broji oko $1 000 000$ jedinki i da populacija raste $10 %$ godišnje.

Prepišite sljedeću tablicu i popunite je za idućih pet godina.

Godine od 2016.	$0$	$1$	$2$	$3$	$4$	$5$
Populacija u milijunima	$1$

Napišite jednadžbu populacije Logaritmije u ovisnosti o broju godina.
Kolika je populacija 2017.? Koliko će jedinki biti na Logaritmiji 2020. godine?
Prikažite funkciju grafički.
Kad će populacija biti $2$ milijuna?

$P = {1.1}^{t}$
2017. populacija je $1.1$ milijun. 2020. bit će $1.46$ milijuna jedinki.
Slika
Za $7.3$ godine.

Zadatak 3.

Pacijent je dobio dozu lijeka od $300 mg .$ Količina lijeka se smanjuje $20 %$ po satu.

Koliko je lijeka nakon $2$ sata preostalo u krvi pacijenta?
Koliko ga je preotalo nakon $5$ sati?
Kao i u prošlom zadatku, popunite sličnu tablicu i napišite kako količina lijeka ovisi o vremenu.
Medicinska sestra treba pacijentu ponovno dati lijek kad ga u krvi bude $10 mg .$ Kad je to?

$192$
$98.304$
$f (x) = 300 \cdot {0.8}^{t}$
Nakon $15.3$ sati.

Zanimljivost

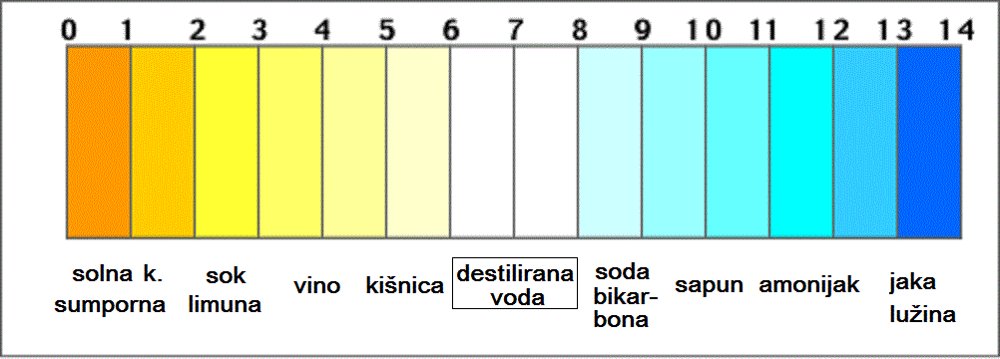
Već smo spominjali pH. Pojasnimo taj pojam još malo. pH je zapravo koncentracija vodikovih iona, a njihova koncentracija nam otkriva je li otopina kisela ili lužnata. Kako je pH vrlo velik ili vrlo malen broj, rabimo logaritamsku skalu ili ljestvicu o kojoj smo također govorili.

pH skala ima raspon od $0$ do $14 .$ Ako je pH $7,$ otopina je neutralna. Čista voda ima $pH = 7 .$ Ako je pH veći od $7,$ otopina je lužnata. Što je pH manji, to je otopina kiselija.

pH se mjeri za tlo, vodu, krv, urin i mnoge druge otopine. pH je važna vrijednost koja ima značenje i posljedice. Na primjer, pH normalne ljudske krvi i tkiva je oko $7,4$ ; ako se taj pH promijeni za $0,2$ ili više, gore ili dolje, to je za život opasna promjena. Idealan raspon za pH vode u bazenu je od $7,2$ do $7,8 .$ Kad pH vode u bazenu padne ispod $7,2,$ ljudi doživljavaju iritaciju očiju i kože, a oprema bazena korodira. Razine iznad $7,8$ inhibiraju sposobnost klora da neutralizira viruse, bakterije i druge zdravstvene rizike u vodi te također uzrokuju iritaciju očiju.

Zadatak 4.

$p H = \log [H^{+}]$

Ako uzorak tekućine ima $p H = 5$ kolika je koncentracija vodikovih iona?
Koliko puta je koncentracija vodikovih iona veća u tekućini s $p H = 5$ od one s $p H = 7 ?$
Koncentracija vodikovih iona u pitkoj vodi je između $3.16 \cdot 10^{- 9}$ i $10^{- 6} .$ Postavite nejednakost i odredite granice pH za pitku vodu.
Koncentracija vodikovih iona u otpini je $10^{- 4} .$ Je li ta otopina više ili manje kisela od vode za piće?

${10^{-}}^{5}$
$100$ puta
između $6$ i $8.5$
$p H = 4 .$ Ta je tekućina kiselija od vode.

Zatvori

Kutak za znatiželjne

Riješimo zadatak s Kineske matemtičke olimpijade.

Ako je $\log_{4} (x + 2 y) + \log_{4} (x - 2 y) = 1,$ koliki je minimum izraza $|x| - |y| ?$

Rješenje i postupak:

Prvo postavimo nejednadžbe i jednadžbu:

$x + 2 y > 0$

$x - 2 y > 0$

$(x + 2 y) (x - 2 y) = 4$

Iz ovih nejednadžbi zaključujemo:

$x > 2, |y| \geq 0, x^{2} - 4 y^{2} = 4$ i da je dovoljno pronaći minimalnu vrijednost za $x - y .$ Zamijenimo li $x - y$ sa $u$ i zamijenimo u $x^{2} - 4 y^{2} = 4,$ imamo jednadžbu:

$3 y^{2} - 2 u y + (4 - u^{2}) = 0$

Ova jednadžba ima realna rješenja zbog uvjeta za y, pa možemo pisati:

$4 u^{2} - 12 (4 - u^{2}) \geq 0,$ pa je zbog toga $u \geq \sqrt{3} .$

Iz toga slijedi da je minimalna vrijednost traženog izraza $\sqrt{3} .$

Kutak za znatiželjne

Ako su $a,$ $b,$ $c,$ $d$ pozitivni brojevi i $\log_{a} b = \frac{3}{2},$ $\log_{c} d = \frac{5}{4}$ te $a - c = 9,$ koliko je $b - d ?$

$93$

Kutak za znatiželjne

Riješite nejednadžbu $\begin{array}{l} \sqrt{\log_{2} x - 1} + \frac{1}{2} \log_{\frac{1}{2}} x^{3} + \frac{3}{2} + \frac{1}{2} > 0 \end{array}$

$2 \leq x < 4$

Na početku...

Zadatak 1.

Samostalne aktivnosti-istražimo!

Praktična vježba

Kolekcija zadataka 1

Zadatak 2.

Zadatak 3.

Zanimljivost

Zadatak 4.

Kutak za znatiželjne

Kutak za znatiželjne

Kutak za znatiželjne

...i na kraju