Aktivnosti za samostalno učenje

Platonova tijela

Platonova su tijela pravilni poliedri, tj. uglata geometrijska tijela kojima su sve strane sukladni pravilni mnogokuti pri čemu se u svakom vrhu siječe isti broj strana. Kutovi među stranama jednakih su veličina.

Postoji pet Platonovih tijela: tetraedar, kocka (heksaedar), oktaedar, dodekaedar i ikosaedar.

Nazvana su po Platonu koji o njima raspravlja u matematičkom dijalogu Timej.

Zanimljivost

Više o Platonu i Platonovim tijelima možete pročitati na mrežnim stranicama Hrvatske enciklopedije.

​

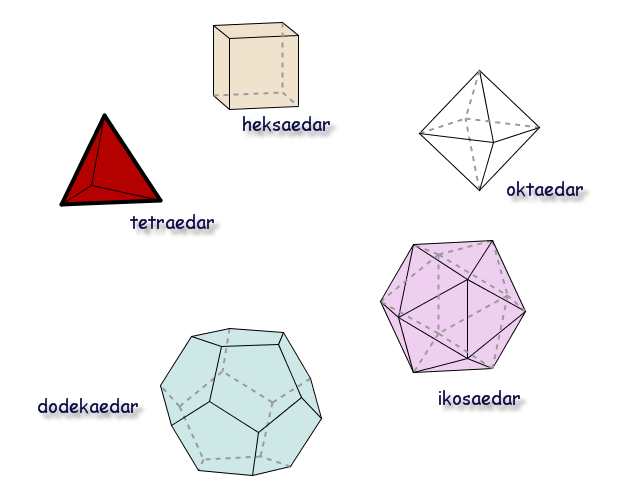
U animaciji koja slijedi pogledajte Platonova tijela i njihove mreže.

Platonovo tijelo	strana (vrsta mnogokuta)	broj strana	grčki naziv broja koji odgovara broju strana	naziv Platonova tijela
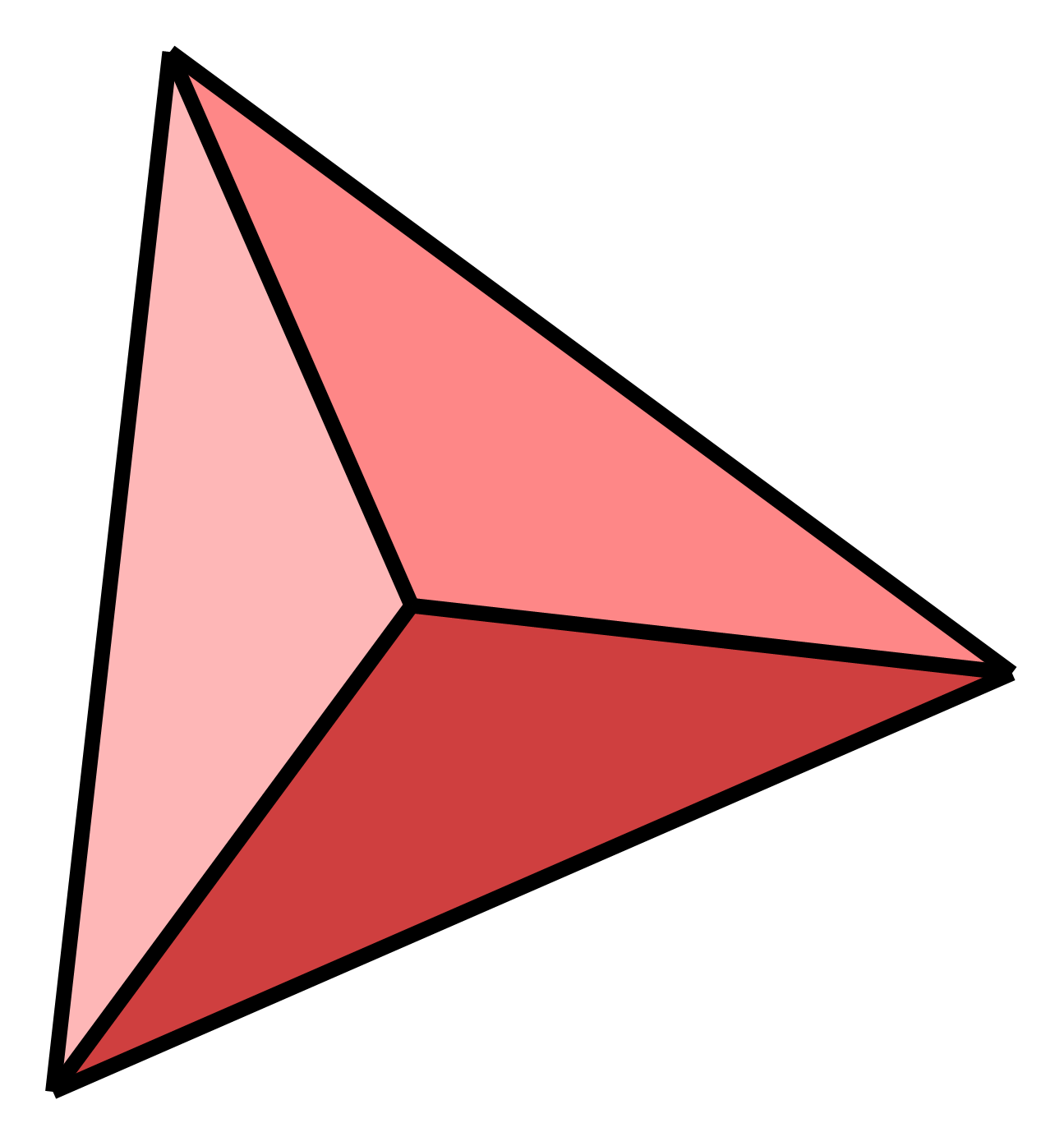
	jednakostranični trokut	$4$	tetra	tetraedar
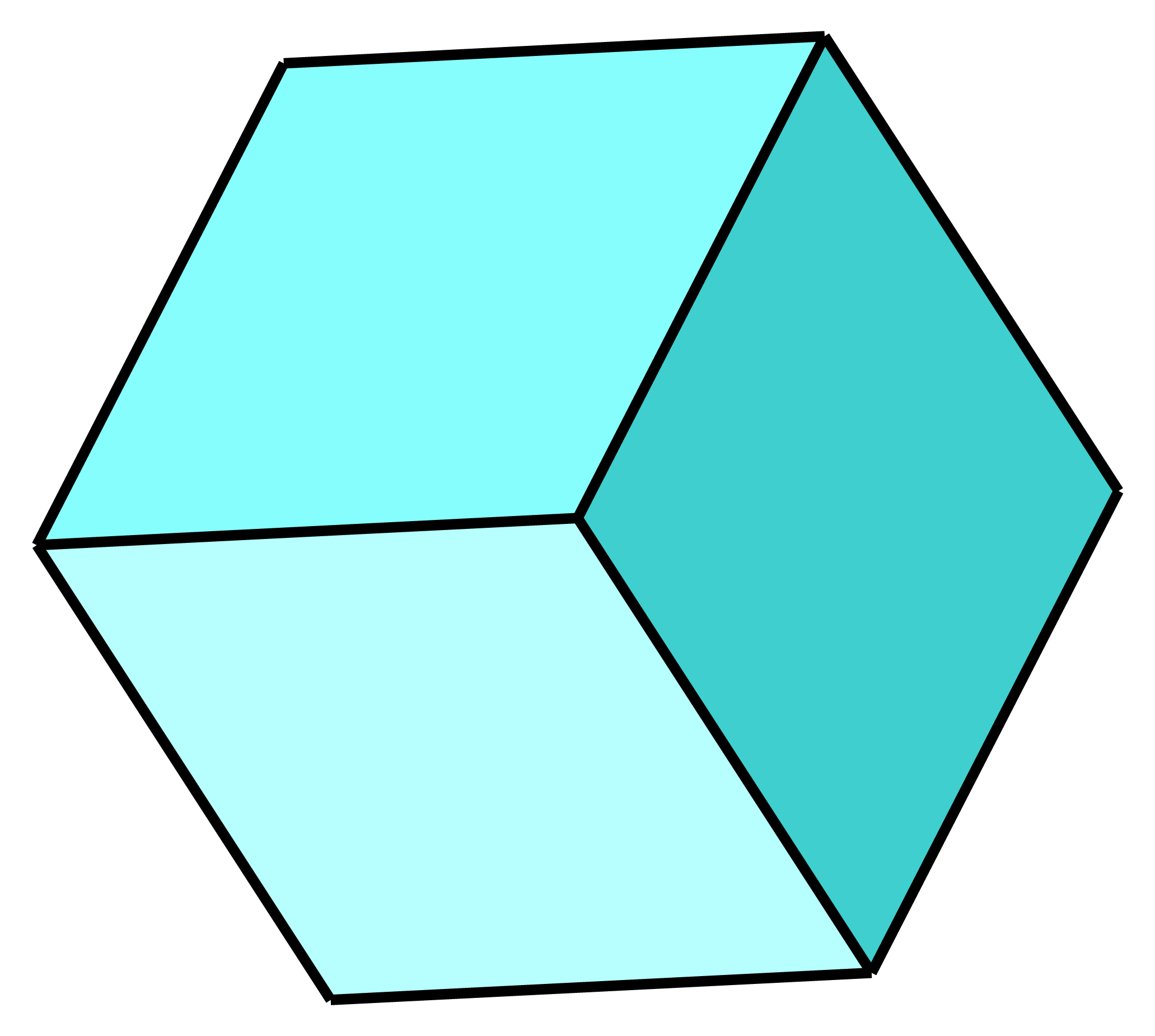
	kvadrat	$6$	heksa	heksaedar
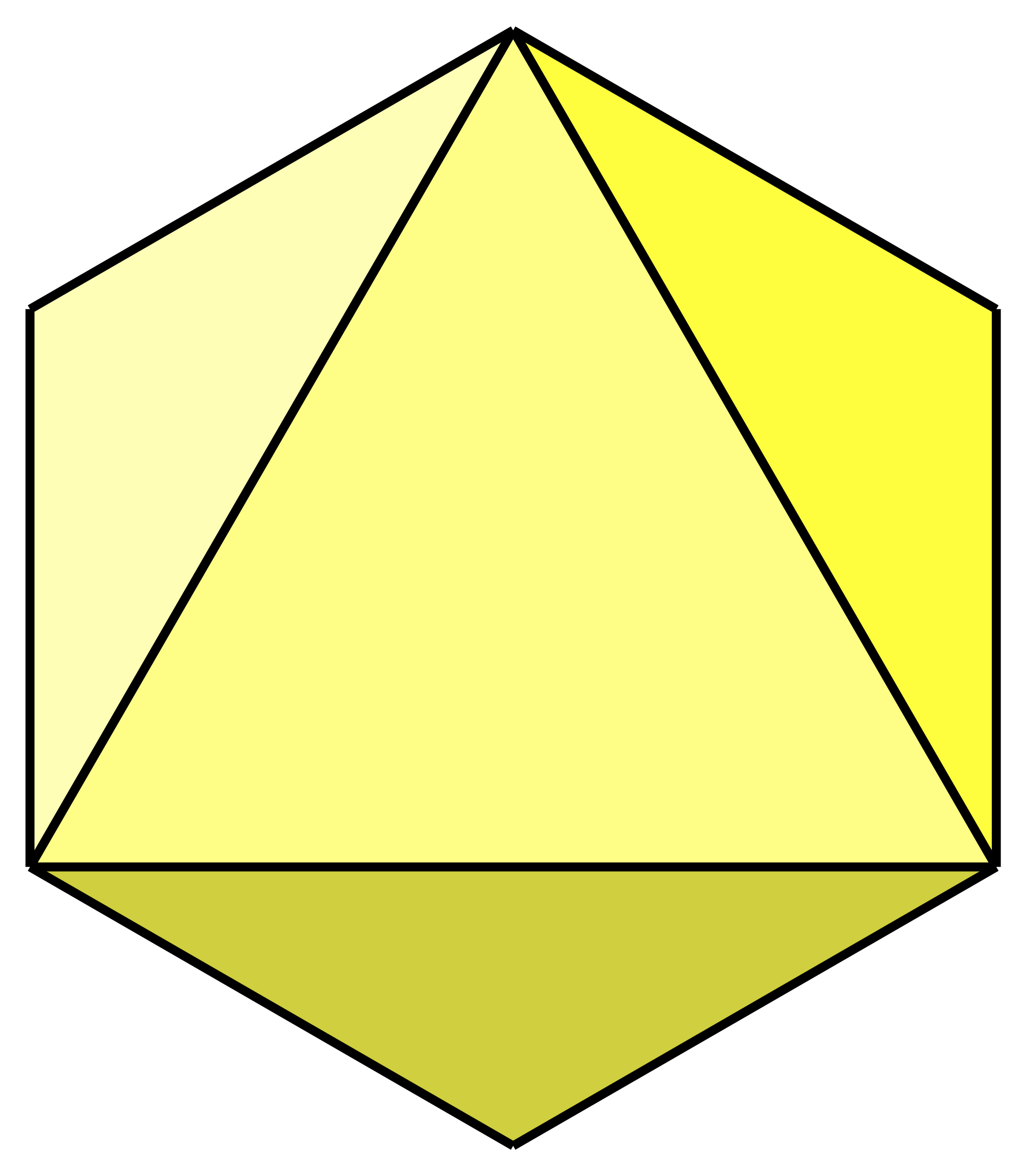
	jednakostranični trokut	$8$	okto	oktaedar
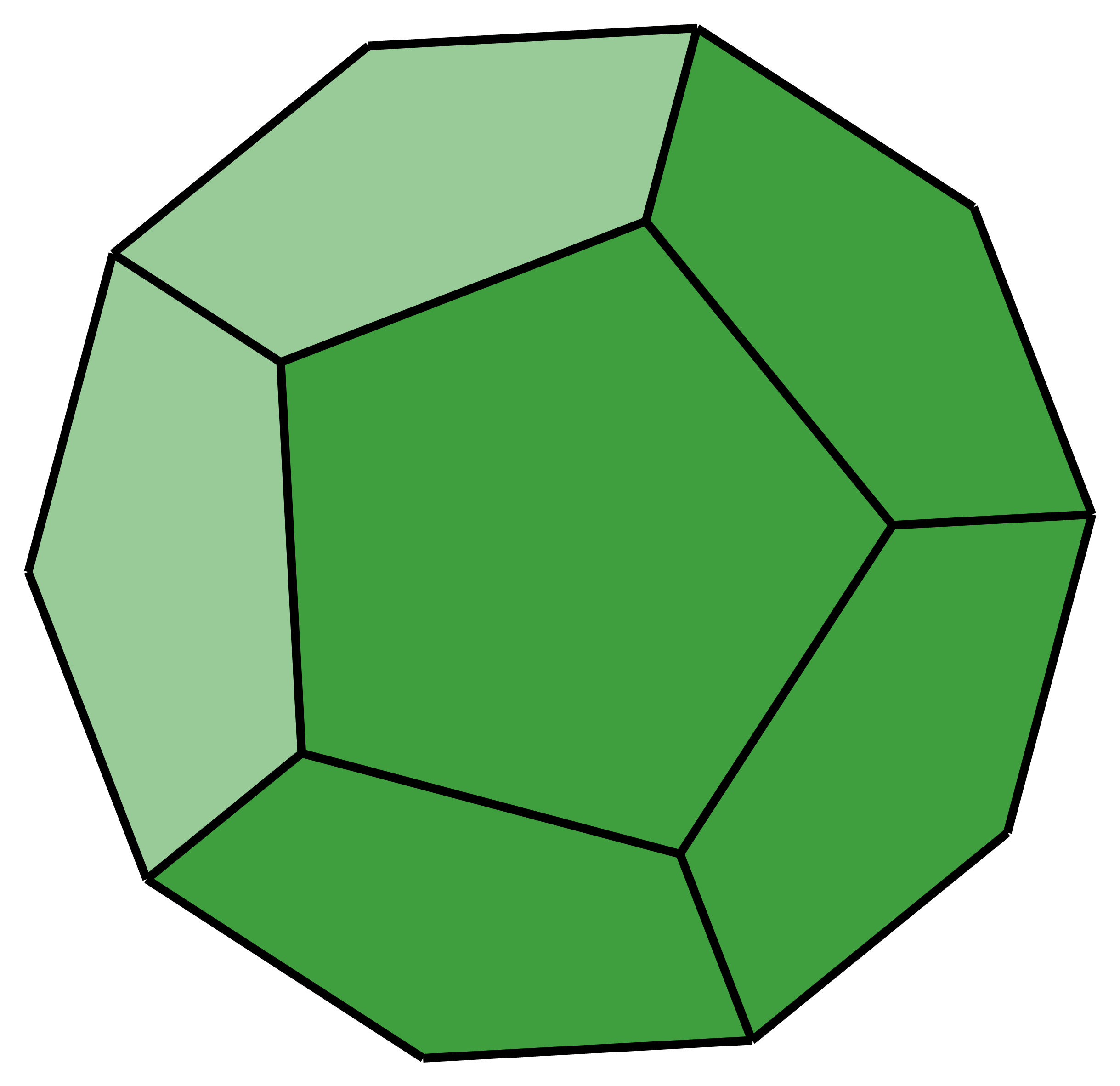
	pravilni peterokut	$12$	dodeka	dodekaedar
	jednakostranični trokut	$20$	ikosi	ikosaedar

 ​

Kolekcija zadataka 1

Zadatak 2.

Promotrite Platonova tijela. Što možete reći o stranama tih tijela? A o bridovima?

Rješenje

Strane svakog tijela sukladni su mnogokuti. Ti su mnogokuti ili jednakostranični trokuti ili kvadrati ili pravilni peterokuti. Svi su bridovi svakog od Platonovih tijela međusobno sukladni, tj. istih su duljina.

---

Zadatak 3.

Povežite Platonovo tijelo s njegovom odgovarajućom mrežom.

	tetraedarikosaedaroktaedardodekaedarheksaedar (kocka)
	tetraedarikosaedaroktaedardodekaedarheksaedar (kocka)
	tetraedarikosaedaroktaedardodekaedarheksaedar (kocka)
	tetraedarikosaedaroktaedardodekaedarheksaedar (kocka)
	tetraedarikosaedaroktaedardodekaedarheksaedar (kocka)

null

null

Zadatak 4.

Prepišite i popunite tablicu u bilježnicu.

Platonovo tijelo	tetraedar	heksaedar (kocka)	oktaedar	dodekaedar	ikosaedar
broj strana
broj vrhova
broj bridova

Što primjećujete?

Rješenje

Platonovo tijelo	tetraedar	heksaedar (kocka)	oktaedar	dodekaedar	ikosaedar
broj strana	$4$	$6$	$8$	$12$	$20$
broj vrhova	$4$	$8$	$6$	$20$	$12$
broj bridova	$6$	$12$	$12$	$30$	$30$

Zbroj broja strana i broja vrhova za dva je veći od broja bridova.

---

Zatvori

Neka je $S$ broj strana, $V$ broj vrhova, a $B$ broj bridova nekoga uglatoga geometrijskog tijela. Tada vrijedi $S+V=B+2,$ tj.

$S+V-B=2.$

Ta je formula poznata pod nazivom Eulerova formula.

Arhimedova tijela

Zanimljivost

 Više o Arhimedu pročitajte na mrežnim stranicama Hrvatske enciklopedije.

Arhimedova su tijela uglata geometrijska tijela kojima strane čine dvije ili više različitih vrsta pravilnih mnogokuta, pri čemu se u svakom vrhu siječe isti broj i ista kombinacija strana.

Postoji ukupno $13$ Arhimedovih tijela, a najpoznatije je tijelo nogometna lopta, koja se sastoji od $20$ pravilnih šesterokuta i $12$ pravilnih peterokuta.