

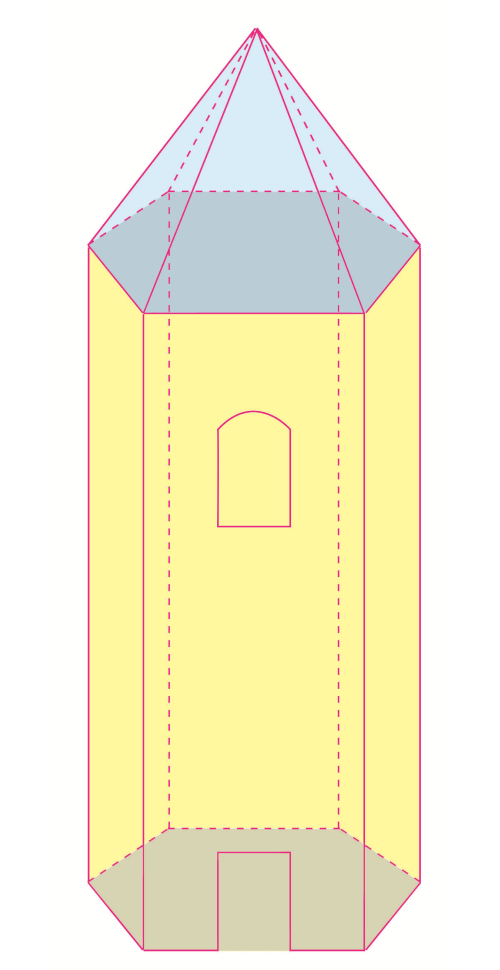
Krov kule ima oblik pravilne piramide. U njegovu je pobočju šest sukladnih jednakokračnih trokuta. Što je baza te piramide? Kako nazivamo takve piramide?
Baza je te piramide pravilni šesterokut.
Takve piramide nazivaju se pravilne (uspravne) šesterostrane piramide.
Koristeći sljedeću interakciju, istražite pravilnu šesterostranu piramidu. Koristite mogućnost promjene visine i rotacije nacrtane piramide.
Uspravnu piramidu kojoj je baza pravilni šesterokut nazivamo pravilna šesterostrana piramida.
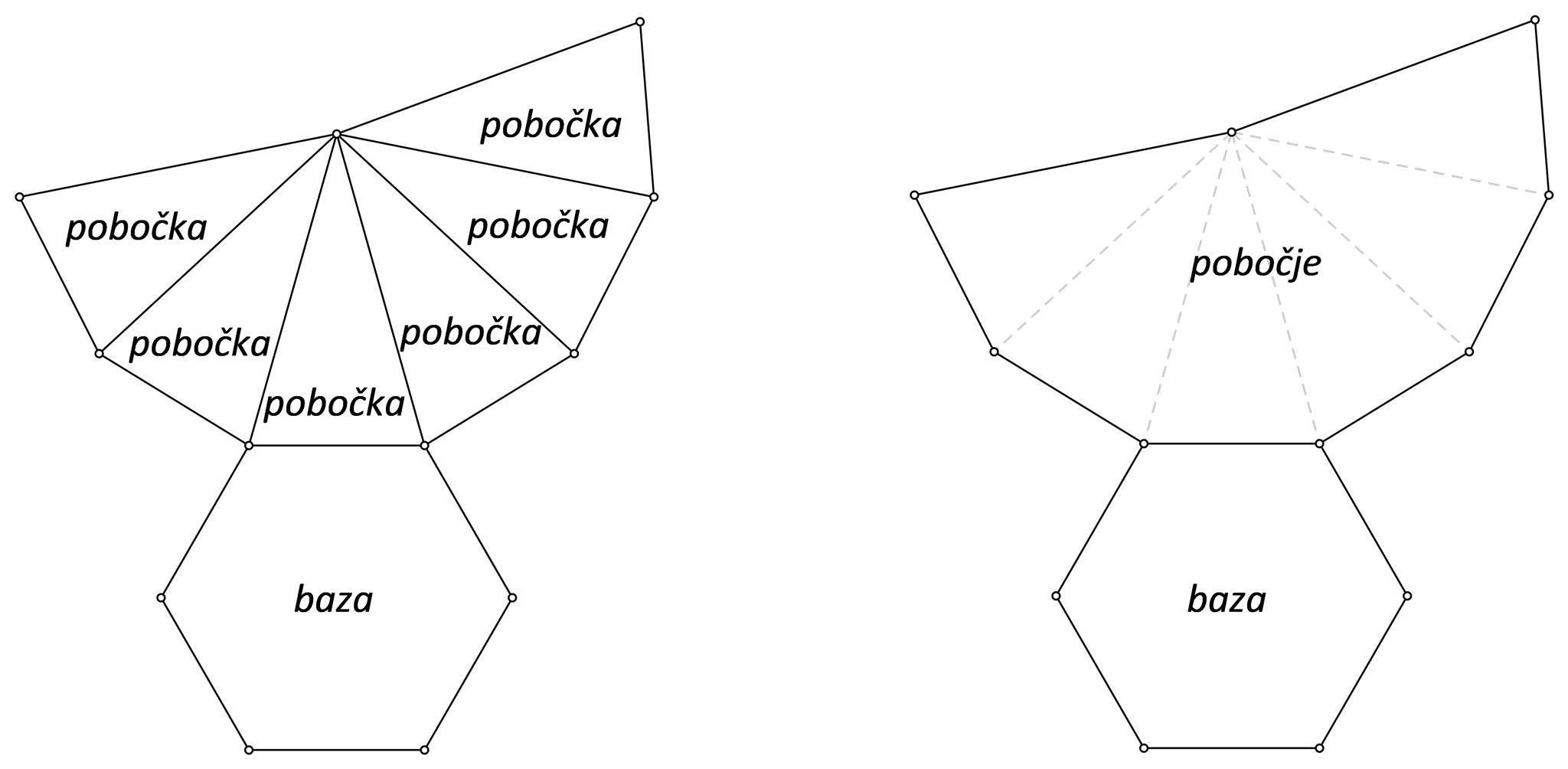
Mreža pravilne šesterostrane piramide sastoji se od jednog pravilnog šesterokuta - to je baza piramide i šest međusobno sukladnih jednakokračnih trokuta - pobočki piramide. Pobočke zajedno čine pobočje piramide.
Primjer 1.
Sljedeća interakcija omogućava prikaz nastajanja jedne od mogućih mreža pravilne šesterostrane piramide. Istaknute točke omogućavaju promjenu duljine osnovnoga brida i visine piramide.
Primjer 2.
Animacija prikazuje još neke mreže pravilne šesterostrane piramide.
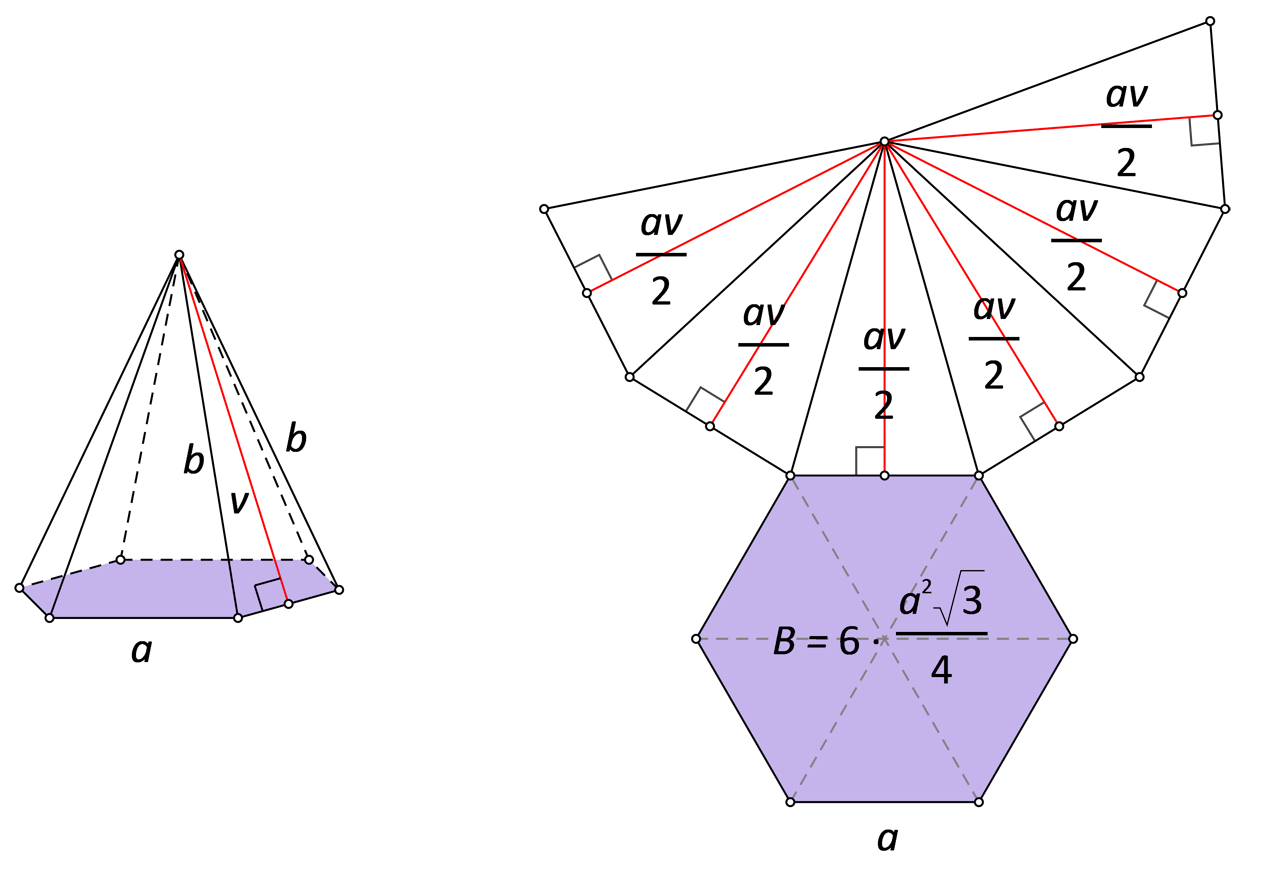
Baza je pravilne šesterostrane piramide pravilni šesterokut sa stranicom duljine pa je površina baze jednaka
Pobočke pravilne šesterostrane piramide sukladni su jednakokračni trokuti s osnovicama duljine i visinom na osnovicu duljine pa je površina svakoga od njih jednaka
Površina pobočja pravilne šesterostrane piramide jednaka je tj.
Oplošje pravilne šesterostrane piramide (kao i svake uspravne piramide) računa se prema formuli
Primjer 3.
Opseg je baze pravilne šesterostrane piramide a duljina je visine pobočke te piramide
Koliko je oplošje te piramide?

Baza je te piramide pravilni šesterokut pa je njegov opseg šest puta dulji od stranice. Dakle, duljina je osnovnog brida te piramide tj.
Površina baze tada se računa kao
pa uvrštavanjem dobivamo da je
tj.
Površina pobočja računa se kao
i jednaka je
Tada je oplošje piramide jednako
Uvrštavanjem dobivamo da je tj. približno
Duljina je osnovnoga brida pravilne šesterostrane piramide a duljina je bočnoga brida Koliko je oplošje ove piramide?
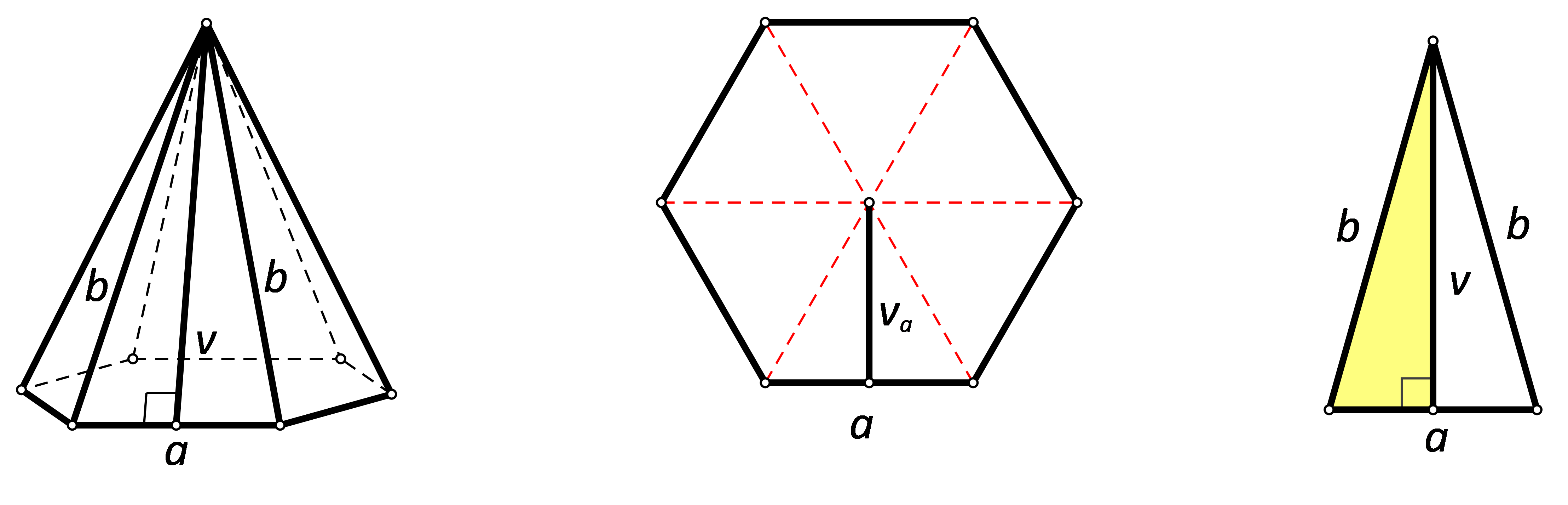
Baza je pravilne šesterostrane piramide pravilni šesterokut sa stranicom duljine
, pa je površina baze jednaka
Uvrštavanjem dobivamo da je
što je približno
Primjenom Pitagorina poučka na polovinu jednakokračnog trokuta (pobočke), uz oznake kao na slici, dobivamo Uvrštavanjem zadanih podataka dobivamo da je tj.
Površinu pobočja računamo kao pa nakon uvrštavanja dobivamo da je ta površina
Oplošje je te piramide što je približno
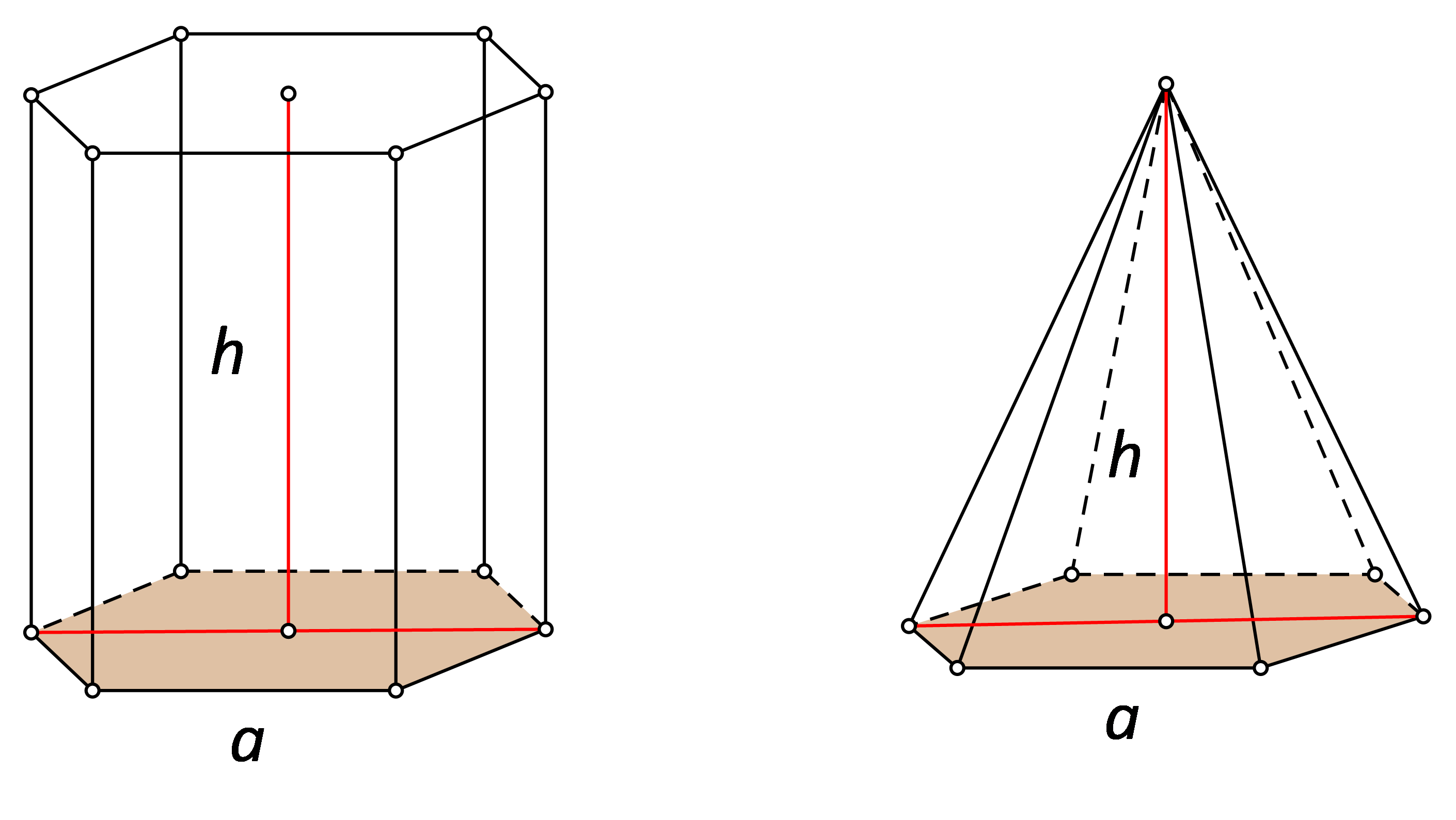
Volumen pravilne šesterostrane piramide računamo (kao i volumen svake uspravne piramide) kao trećinu umnoška površine baze i duljine visine, tj. prema formuli
Primjer 4.
Duljina je osnovnog brida pravilne šesterostrane piramide a duljina njezine visine Koliki je volumen ove piramide?
Površina baze računa se kao pa uvrštavanjem dobivamo da je što je približno
Uvrštavanjem odgovarajućih podataka u izraz za volumen piramide
dobivamo da je
što je približno
Površina je baze pravilne šesterostrane piramide a njezino je oplošje Koliki je volumen te piramide?
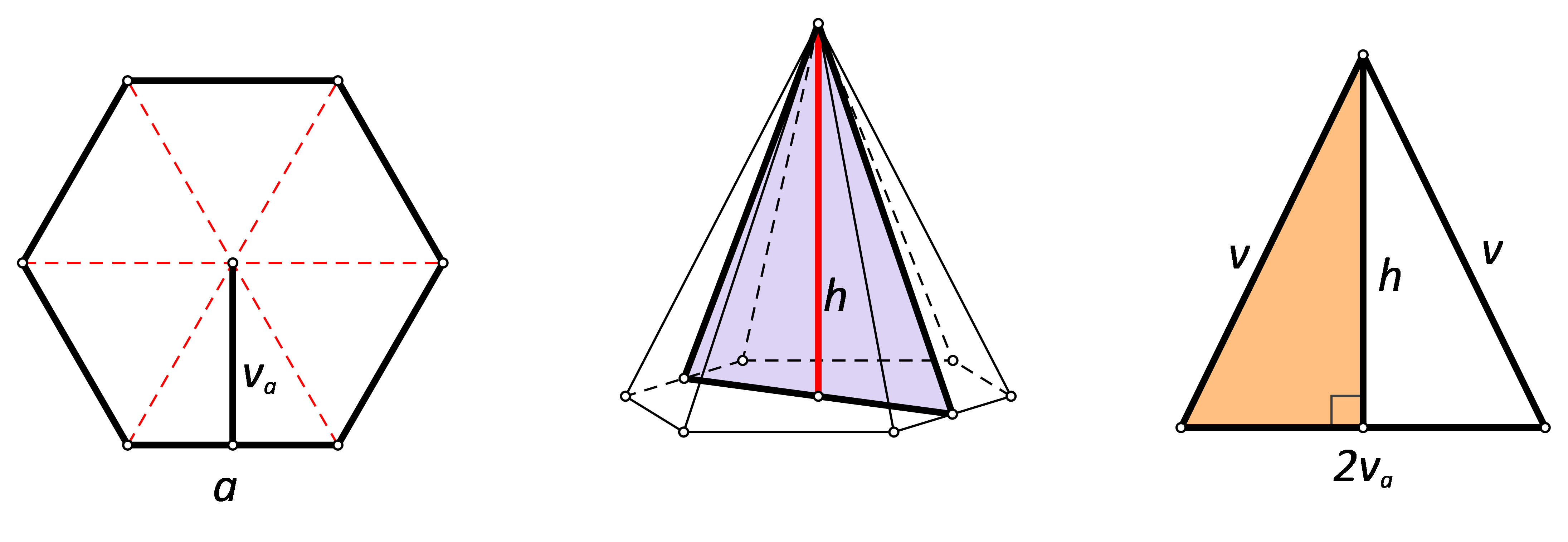
Površina baze računa se kao pa uvrštavanjem dobivamo da je te je i
Oplošje piramide računa se po formuli
te je površina pobočja
Iz formule za površinu pobočja
dobivamo da je
tj. da je
Primjenom Pitagorina poučka na trokut koji povezuje visinu piramide, visinu karakterističnog trokuta pravilnog šesterokuta koji sačinjava bazu te visine trokuta pobočke, dobivamo da je
S obzirom na to da je
slijedi
i

Drugi način određivanja visine piramide i njezina volumena:
Iz formule za površinu pobočja
dobivamo da je
tj. da je
Primjenom Pitagorina poučka na trokut koji povezuje visinu piramide, duljinu bočnog brida i duljinu stranice karakterističnog trokuta pravilnog šesterokuta dobivamo da je odakle uvrštavanjem nalazimo da je
Volumen određujemo kao u prethodnom načinu rješavanja.
Duljina je osnovnoga brida pravilne šesterostrane piramide
a duljina visine njezine pobočke
Izračunajte volumen te piramide.
Visina karakterističnog trokuta baze iznosi
Primjenom Pitagorina poučka na trokut koji povezuje visinu piramide, visinu karakterističnoga trokuta pravilnoga šesterokuta koji sačinjava bazu te visine trokuta pobočke, dobivamo da je tj. da je
Iz slijedi da je
Duljina pobočnoga brida pravilne šesterostrane piramide može biti jednaka duljini osnovnoga brida.
Pomoć:
Ako bi u pravilnoj šesterostranoj piramidi vrijedilo da je
, onda bi pobočke te piramide bili jednakostranični trokuti. Ti trokuti bili bi sukladni s karakterističnim trokutima pravilnoga šeterokuta i od njih se ne bi mogla „sagraditi" piramida.
Dvije pravilne šesterostrane piramide imaju sukladne baze, a duljine njihovih visina odnose se kao
Volumen veće piramide
je puta veći od volumena manje piramide.
Dvije pravilne šesterostrane piramide imaju jednake visine, a duljine njihovih osnovnih bridova odnose se kao
Volumen veće piramide
je puta veći od volumena manje piramide.
Pomoć:
Ako se brid pravilnoga šesterokuta utrostruči, njegova će se površina povećati devet puta.
Duljina je osnovnog brida pravilne šesterostrane piramide
a duljina bočnog brida
Koliko je oplošje te piramide?
Površina je pobočja pravilne šesterostrane piramide
a najdulja dijagonala baze duga je
Koliki je volumen te piramide?
Pravilnu šesterostranu piramidu možemo presjeći ravninom koja prolazi njezinim vrhom i dvama nasuprotnim vrhovima baze. Dobiveni će presjek biti jednakokračni trokut s osnovicom duljine i krakovima duljine . Visina na osnovicu tog trokuta je i visina promatrane piramide.
Takav presjek sadrži najdulju dijagonalu baze pa ga zovemo (najveći) dijagonalni presjek pravilne šesterostrane piramide.
Sljedeća interakcija prikazuje presjek pravilne šesterostrane piramide ravninom koja prolazi njezinim vrhom i dvama nasuprotnim vrhovima baze. Rotirajte piramidu kako biste bolje uočili nastali presjek. Interakcija će vam pomoći u rješavanju zadataka koji slijede.
Duljina je osnovnog brida pravilne šesterostrane piramide Ta je piramida presječena ravninom koja prolazi njezinim vrhom i dvama nasuprotnim vrhovima baze. Površina je dobivenog presjeka Koliki je volumen te piramide?
Površina presjeka pravilne šesterostrane piramide koji prolazi vrhovima piramide i dvama nasuprotnim vrhovima baze računa se prema formuli
tj.
Iz toga slijedi da je
i
Površina baze piramide iznosi
a obujam
Najveći je dijagonalni presjek pravilne šesterostrane piramide jednakostraničan trokut čija je površina jednaka Izračunajte volumen te piramide.
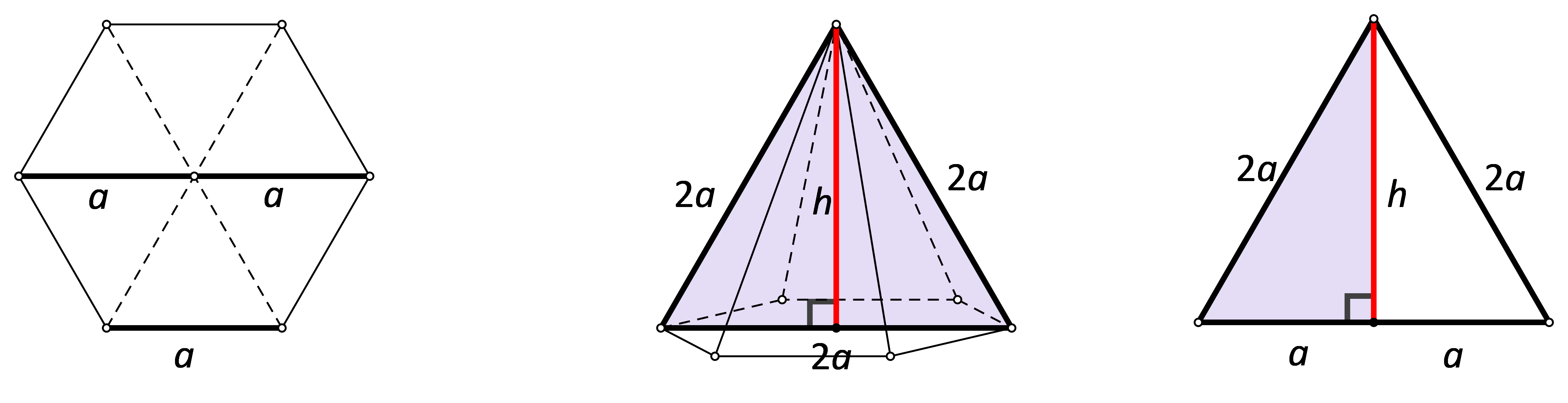
Formula za površinu najvećeg dijagonalnog presjeka pravilne piramide u obliku jednakostraničnog trokuta je .
Iz toga slijedi da je a zatim i
Visina te piramide jednaka je visini jednakostraničnog trokuta presjeka te piramide, tj. Stoga je
Volumen pravilne šesterostrane piramide računa se prema formuli tj.
Sljedeća interakcija prikazuje presjek pravilne šesterostrane piramide ravninom koja prolazi njezinim vrhom i polovištima dvaju nasuprotnih bridova baze. Rotirajte piramidu kako biste bolje uočili nastali presjek. Interakcija će vam pomoći u rješavanju zadatka koji slijedi.Pravilnu šesterostranu piramidu možemo presjeći ravninom koja prolazi njezinim vrhom i polovištima dvaju nasuprotnih bridova baze. Dobiveni će presjek biti jednakokračni trokut s osnovicom duljine i krakovima duljine Visina na osnovicu tog trokuta je i visina promatrane piramide.
Površina je pobočja pravilne šesterostrane piramide a duljina visine njezine pobočke Ta je piramida presječena ravninom koja je određena njezinim vrhom i polovištima dvaju nasuprotnih bridova baze. Kolika je površina tog presjeka?
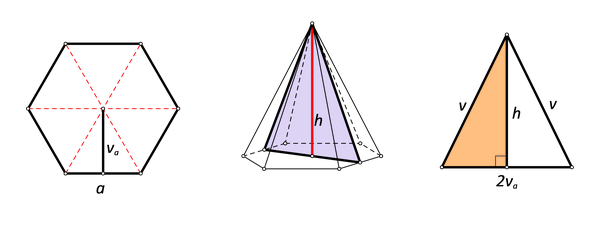
Formula za pobočje pravilne šesterostrane prizme je
Iz toga slijedi i
Visina karakterističnog trokuta baze iznosi
Primjenom Pitagorina poučka na pravokutni trokut koji povezuje visinu pobočke, visinu piramide i visinu karakterističnog trokuta baze, dobivamo
Površina dijagonalnog presjeka iznosi
Čaša za sladoled ima oblik pravilne šesterostrane piramide. Duljina je osnovnog brida čaše 6 cm, a duljina bočnog brida 10 cm. Koliki je volumen čaše?

Sjenilo svjetiljke ima oblik pravilne šesterostrane piramide s osnovnim bridom duljine i bočnim bridom duljine Kolika je površina materijala potrebna za njegovu izradu?
Površina materijala jednaka je površini pobočja.
Primjenom Pitagorina poučka na polovicu trokuta pobočke dobivamo
Površina pobočja jednaka je
U ovoj ste jedinici naučili:
Za kraj, riješite sljedeći zadatak:

Krov je kule u obliku pravilne šesterostrane piramide. Pobočke su te piramide jednakokračni trokuti, pri čemu je duljina osnovice svakoga od tih trokuta jednaka
dok je duljina njihovih krakova
Kolika je površina krova?
Primjenom Pitagorina poučka na polovinu jednakokračnog trokuta s osnovicom duljine
i krakovima duljine
dobivamo da je duljina visine jednakokračnog trokuta (pobočke piramide) jednaka
tj.
Površina svakog od tih trokuta jednaka je približno
pa je površina cijelog krova približno