

Promotrite jednakosti.


Matematika je puna zanimljivih zakonitosti koje se jako lijepo daju opisati.
U ovoj ćete jedinici promatrati i opisati različite zakonitosti te samostalno istraživati nove ideje vezane za kvadriranje.
Gaussova dosjetka
Poznata je anegdota o matematičaru Carlu Friedrichu Gaussu kojem je učitelj zadao izračunati zbroj prvih
brojeva. Na učiteljevo iznenađenje, Gauss je u trenutku došao do točnog rezultata. Naime, on je združio prvi i posljednji broj, drugi i pretposljednji itd. Uočio je da takvih parova ima
te da je zbroj svakog para
Na osnovi toga zaključio je da je zbroj prvih
prirodnih brojeva jednak
Općenito, za zbroj
uzastopnih prirodnih brojeva
vrijedi:

Način na koji je Gauss riješio taj zadatak naziva se Gaussova dosjetka.
Odredite zbroj prvih prirodnih brojeva.
Zbroj prvih brojeva je
Pogledajmo sada zbrojeve uzastopnih neparnih brojeva.
Uočavamo da je zbroj prvih uzastopnih neparnih prirodnih brojeva jednak kvadratu prirodnog broja Provjerimo zbog čega je to tako.
Kako bismo dobili niz od neparnih članova iz niza uzastopnih prirodnih brojeva, morali smo oduzeti sve parne brojeve. Zato je takav niz morao sadržavati članova (posljednji je broj tog niza neparan), a vrijednost je njegova posljednjeg člana
Odrediti zbroj prvih uzastopnih neparnih prirodnih brojeva znači izračunati zbroj
Vidimo da u prvih neparnih prirodnih brojeva ima parova, a zbroj je svakog para Zato je zbroj prvih uzastopnih neparnih prirodnih brojeva jednak
Uočimo.
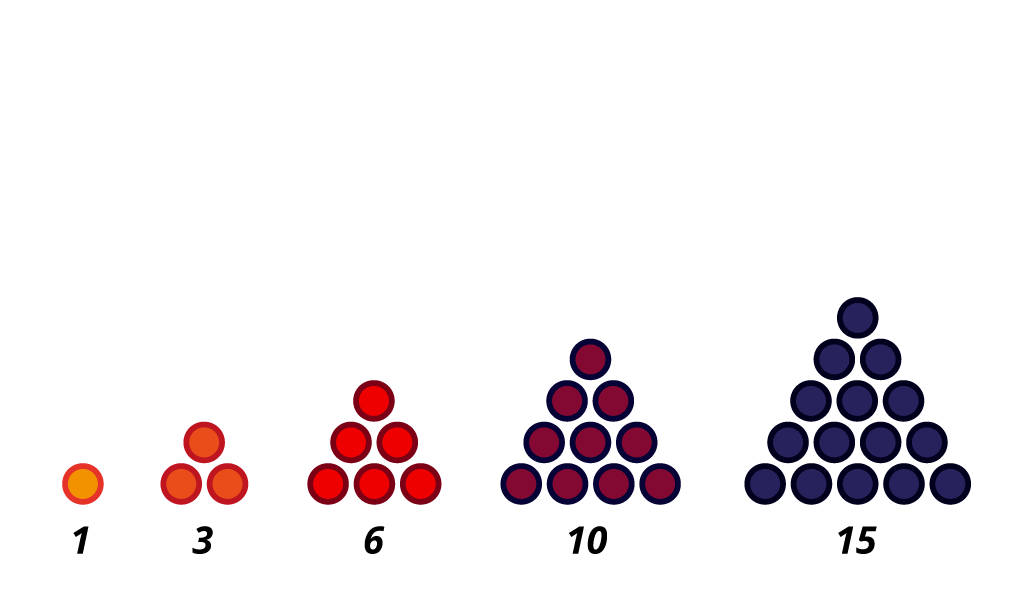
Prirodne brojeve možemo predočiti na geometrijski način. Primjerice, od određenog broja točkica možemo složiti različite oblike kao što su trokuti ili kvadrati. Tako nastaje, primjerice, niz trokutastih brojeva
… i niz kvadratnih brojeva
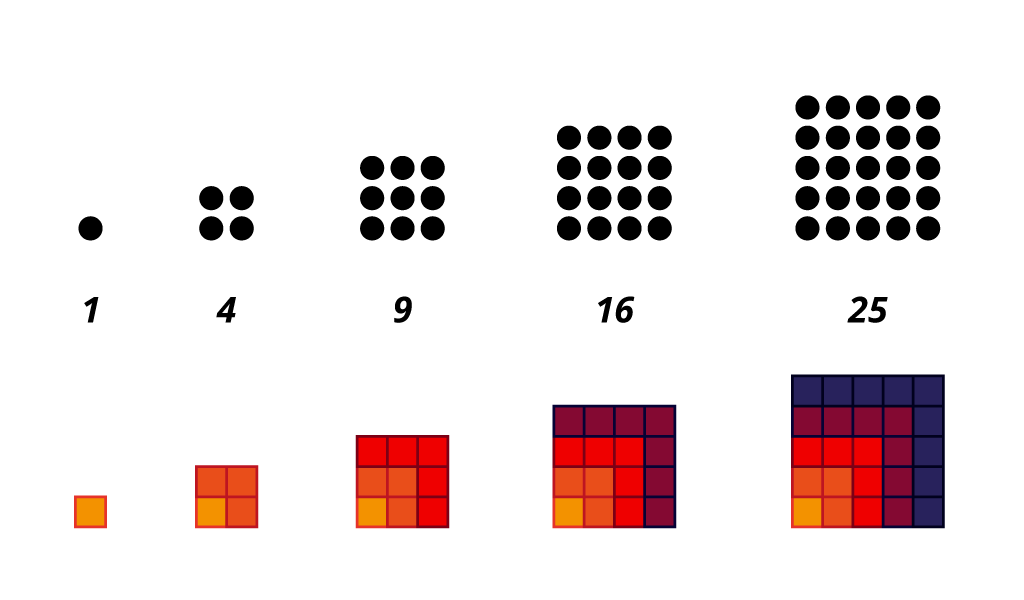
Odredite sljedeća dva člana niza trokutastih brojeva
Odredite sljedeća dva člana niza kvadratnih brojeva
Vrijednost svakog člana niza jednaka je kvadratu njegova rednoga broja u nizu. Zato je šesti član toga niza a sedmi
Kolika je vrijednost
člana niza kvadratnih brojeva?
Vrijednost je člana niza
Promotrimo brojeve i i njihove kvadrate.
Provjerite zbrojeve znamenaka dobivenih kvadrata. Što zamjećujete?
Zbroj znamenaka kvadrata broja je a zbroj znamenaka kvadrata broja je Zgodno, zar ne?
Rina promatra brojevne izraze s prirodnim brojevima...
Nakon nekoliko primjera uočava da ako pomnoži dva broja koja se razlikuju za dva te umnožak uveća za jedan, zbroj je jednak kvadratu broja između početnih dvaju brojeva. Zanima je vrijedi li to uvijek?
Pretpostavimo da je srednji broj jednak n. Izraze koje tada promatra može zapisati u obliku
Iz toga slijedi da je
Dakle, zakonitost koju je uočila na tih nekoliko jednakosti vrijedit će za sve takve izraze s prirodnim brojevima.
Promotrite, istražite i opišite zakonitost.
Rješavanjem svakog od zadanih izraza dobivamo kvadrat nekoga prirodnog broja. Ako pretpostavimo da je prvi broj tada možemo pisati:
Ako pretpostavimo da je drugi broj tada možemo pisati:
Postoji li prirodni broj čija je dvostruka vrijednost jednaka njegovu kvadratu? Objasnite.
Ako podijelimo obje strane jednakosti brojem dobivamo da je
Dvostruka vrijednost broja dva je što je jednako kvadratu broja 2 , tj. vrijedi:
Postoji li broj čija je dvostruka vrijednost veća od njegova kvadrata? Objasnite.
Ako obje strane jednakosti podijelimo brojem dobivamo
Postoji samo jedno rješenje, a to je broj
Dvostruka vrijednost broja veća je od kvadrata broja
Ako neki broj povećamo šest puta, za koliko će se puta povećati njegov kvadrat?
Ako neki broj povećamo šest puta, dobit ćemo broj Nakon što kvadriramo, dobit ćemo Zato će se kvadrat tog broja povećati puta.
Koliko se promijeni površina kvadrata ako njegovu stranicu najprije povećamo za a zatim smanjimo za
Ako stranicu kvadrata povećamo za
duljina njegove stranice bit će
Nakon što smanjimo duljinu te stranice za
duljina stranice konačnog kvadrata iznosit će
Površina tog kvadrata iznosit će
Dakle, ukupna se površina smanjila za
Na crtu upišite odgovarajući broj.
Omjer je duljina stranica dvaju kvadrata U kojem su omjeru njihove površine?
Omjer njihovih površina bit će
Površine dvaju kvadrata razlikuju se za a duljine njihovih stranica izražene su prirodnim brojevima (u centimetrima). Kolike su duljine stranica tog kvadrata?
Pretpostavimo da je duljina dulje stranice a kraće Tada vrijedi S obzirom na to da je broj prikazat ćemo u obliku umnoška dvaju prirodnih brojeva (od kojih je veći jednak vrijednosti a manji vrijednosti ). Broj možemo zapisati kao i pa se zadatak svodi na rješavanje dvaju sustava linearnih jednadžbi:
ili
Rješavanjem prvog sustava dobivamo
a drugog
Zadatak ima dva rješenja: duljine stranica kvadrata mogu biti
i
ili
i
Zbroj kvadrata triju uzastopnih neparnih prirodnih brojeva iznosi . Koji su to brojevi?
To su brojevi i
Složite devet kvadratića tako da svi zadaci i sva rješenja koja se dodiruju odgovaraju.