

Likovi u ravnini mogu, ali ne moraju, biti simetrični. Među simetričnim likovima razlikovali smo osnosimetrične likove i centralnosimetrične likove, pri čemu su neki likovi istodobno mogli biti i osnosimetrični i centralnosimetrični.
Jednostavne geometrijske likove jednostavno je razvrstati prema vrsti simetrije koju imaju. Što reći o sljedećim likovima? Jesu li osnosimetrični? A centralnosimetrični?
Ni jedan od ovih likova nije ni osnosimetričan, ni centralnosimetričan, no oni ipak izgledaju nekako „pravilno“.
Svi ovi likovi u „svojoj sredini“ imaju (na slikama skrivenu) točku oko koje se rotacijom za određeni kut preslikavaju sami na sebe. Za takve likove kažemo da su rotacijski simetrični.
Geometrijski je objekt (figura, lik) u ravnini rotacijski simetričan ako u ravnini postoji rotacija objekta oko neke točke (centra rotacije) kojom se taj objekt preslika sam na sebe.
Rotacijski su simetrični svi pravilni mnogokuti, pri čemu je kut rotacije bilo koji (cjelobrojni) višekratnik središnjeg kuta tog pravilnog mnogokuta.
O rotacijskoj simetriji u ravnini i prostoru pročitajte u članku Izidora Hafnera Rotacijska simetrija, Matka broj 81.
Evo i nekoliko primjera kristalnih struktura koje imaju i svojstvo rotacijske simetrije.
Naučili ste translatirati, zrcaliti i rotirati razne pravilne i nepravilne oblike. U nastavku možete naučiti kako popločiti ravninu koristeći zadane (ili odabrane) oblike i neke od navedenih transformacija.

Popločiti ravninu znači prekriti je u potpunosti sukladnim geometrijskim likovima pri čemu se likovi ne preklapaju.
Crtanjem istražite koji pravilni mnogokuti mogu popločiti ravninu. Objasnite zbog čega.
Pomoću sljedeće interakcije istražite popločivanje ravnine pravilnim mnogokutima.
Ravnina se može popločiti jednakostraničnim trokutima, kvadratima i pravilnim šesterokutima. Ukupan zbroj unutarnjih kutova pravilnog mnogokuta koji se susreću u jednome vrhu mora iznositi
Veličina unutarnjeg kuta jednakostraničnog trokuta iznosi
To znači da će šest jednakostraničnih trokuta pri popločivanju ravnine dijeliti zajednički vrh.
Veličina unutarnjeg kuta kvadrata iznosi
To znači da će četiri kvadrata pri popločivanju ravnine dijeliti zajednički vrh.
Veličina unutarnjeg kuta pravilnog šesterokuta iznosi
To znači da će tri pravilna šesterokuta pri popločivanju ravnine dijeliti zajednički vrh.
Istražite može li se ravnina popločiti koristeći pravilne osmerokute i kvadrate ili jednakostranične trokute i kvadrate. Nacrtajte slike i objasnite.
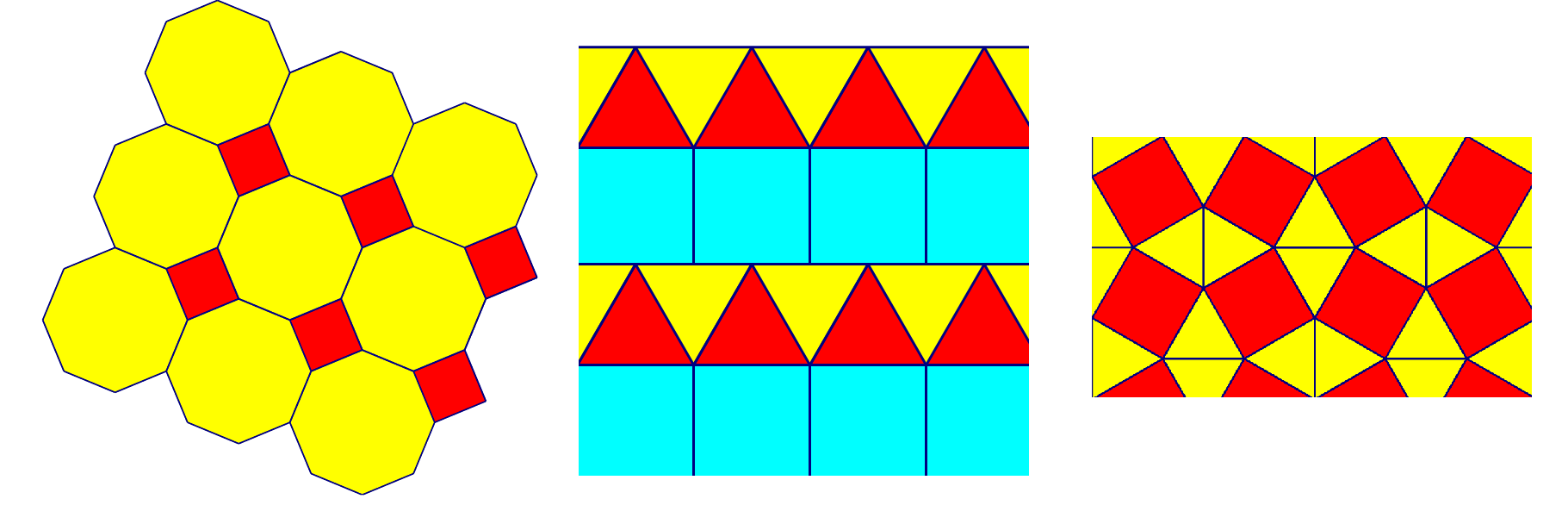
Pravilni osmerokut i kvadrat mogu popločiti ravninu tako da zajednički vrh dijele dva pravilna osmerokuta i jedan kvadrat. Veličina unutarnjeg kuta pravilnog osmerokuta iznosi a kvadrata a
Jednakostranični trokut i kvadrat mogu popločiti ravninu tako da zajednički vrh dijele dva kvadrata i tri jednakostranična trokuta. Veličina unutarnjeg kuta jednakostraničnog trokuta iznosi
a kvadrata
a
Istražite kako pomoću translacije kvadrata i jednakostraničnog trokuta te dizajna nacrtanih unutar njih nastaju zanimljive slike. Za to će vam pomoći aplikacija 1, aplikacija 2 i aplikacija 3.
Pogledajte animaciju koja prikazuje nastajanje popločivanja ravnine nepravilnim oblicima i izradu slike te pokušajte nacrtati vlastiti dizajn.
Geoploča i/ili točkasti papir mogu pomoći vašem boljem snalaženju u preslikavanjima ravnine.
Sljedeće zadatke možete rješavati na točkastom papiru ili geoploči.
Online geoploča dostupna je na sljedećoj poveznici.
Istaknuti je pravac os simetrije. Prikažite trokut tako da se cijeli trokut nalazi s desne strane istaknutog pravca. Prikažite njegovu osnosimetričnu sliku.

Istaknuti je pravac os simetrije. Na geoploči prikažite trokut tako da se jedan njegov vrh nalazi na zadanom pravcu, a dva vrha s lijeve strane zadanog pravca. Prikažite osnosimetričnu sliku tog trokuta.

Na slici je istaknuta os simetrije. Na geoploči prikažite trokut tako da se dva vrha nalaze iznad, a jedan ispod zadanog pravca, Prikažite njegovu osnosimetričnu sliku.

Na slici je istaknuta os simetrije. Na geoploči prikažite neki trokut te njegovu osnosimetričnu sliku.
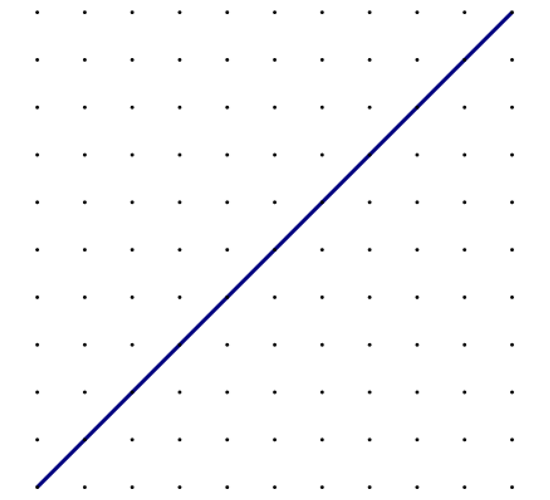
Istaknuti je pravac os simetrije. Koristeći geoploču, dovršite sliku osnosimetričnog lika.

Prikazani su osnosimetrični likovi. Prikažite svakog od njih na geoploči te istaknite njihove osi simetrije.
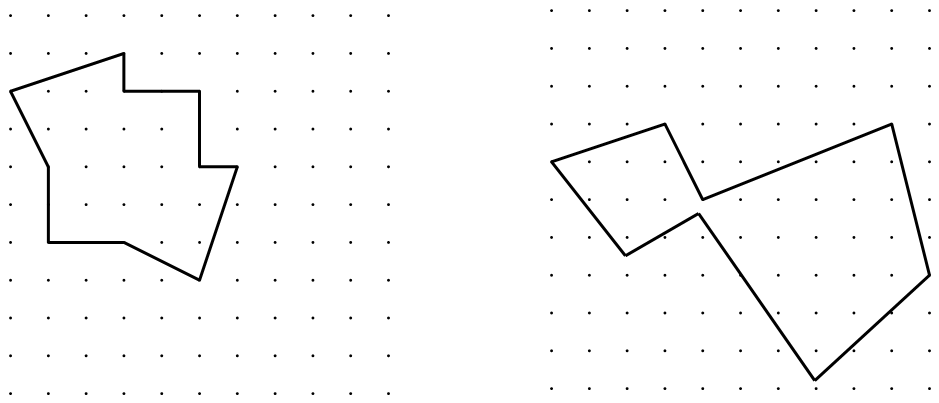
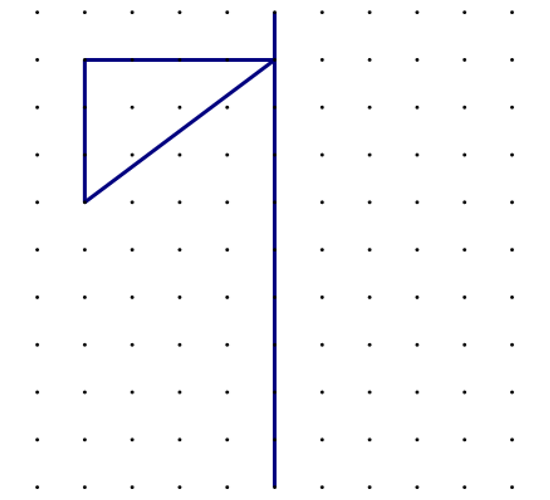
Prikažite osnosimetričnu sliku zadanog trokuta s obzirom na istaknutu os simetrije.
Udaljenost između dva čavlića (točkica) u istome retku ili istome stupcu iznosi 1 jedinicu.
Prikažite osnosimetričnu sliku zadanog četverokuta s obzirom na zadanu os simetrije.
Promotrite, jesu li parovi stranica ostali usporedni nakon što je kvadrat preslikan osnom simetrijom? Što primjećujete?
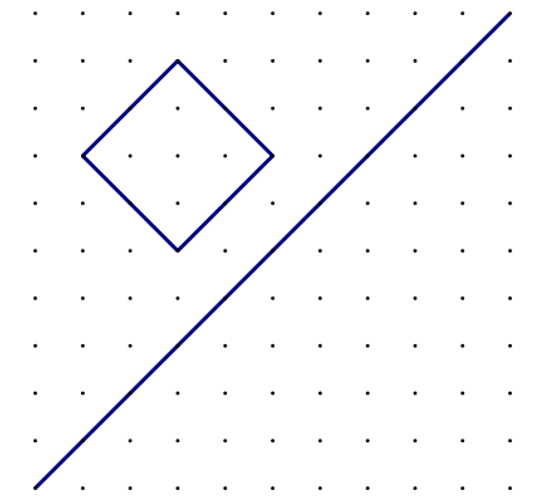
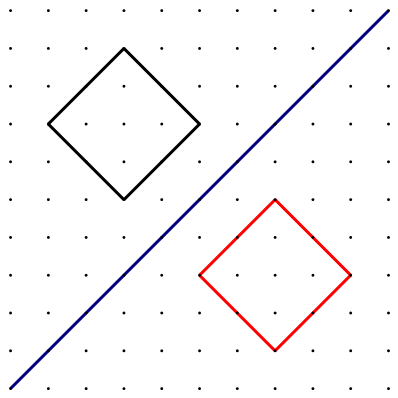
Parovi usporednih stranica ostali su usporedni i nakon preslikavanja. Osna simetrija čuva usporednost pravaca.
Na geoploči prikažite trokut tako da se cijeli nalazi u trećem kvadrantu te ispišite koordinate njegovih vrhova. Preslikajte trokut s obzirom na os
, te ispišite koordinate vrhova preslikanog trokuta. Promotrite, ako mnogokut s vrhom
preslikamo s obzirom na os
kako će se to odraziti na njegove koordinate?

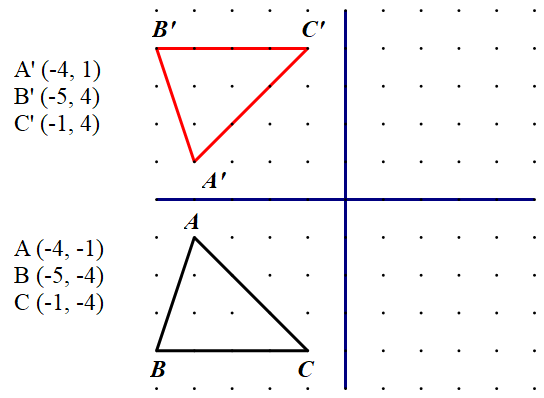
Koordinata ostaje nepromijenjena, dok koordinata mijenja predznak. Osnosimetrična slika točke zadane koordinatom preslikane preko osi ima koordinate
Na geoploči prikažite trokut tako da se cijeli nalazi u drugom kvadrantu te ispišite koordinate njegovih vrhova. Preslikajte trokut s obzirom na os
, te ispišite koordinate vrhova preslikanog trokuta. Promotrite, ako mnogokut s vrhom
preslikamo s obzirom na os
kako će se to odraziti na njegove koordinate?
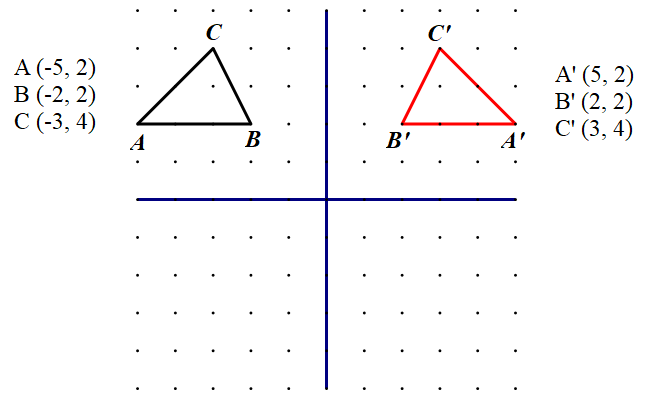
Koordinata ostaje nepromijenjena, dok koordinata mijenja predznak. Osnosimetrična slika točke zadane koordinatom preslikane preko osi ima koordinate
Na geoploči gumicama prikažite trokut s vrhovima Trokut translatirajte za jedinice u smjeru -osi i jedinice u smjeru -osi. Nacrtajte odgovarajuću sliku te odredite koordinate vrhova translatiranog trokuta.
Ako translatirate mnogokut čiji je jedan vrh u
za
jedinice u smjeru
-osi i
jedinice u smjeru
-osi, koje će koordinate poprimiti taj vrh?
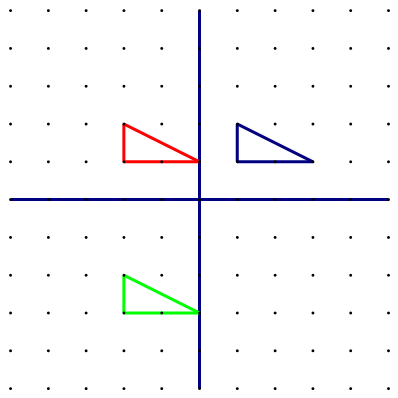
Koordinate trokuta su
Ako translatiramo mnogokut za
jedinice u smjeru
-osi i
jedinice u smjeru
-osi,
koordinata točke smanjit će se za
a
koordinata smanjiti za četiri, tj. poprimit će koordinate
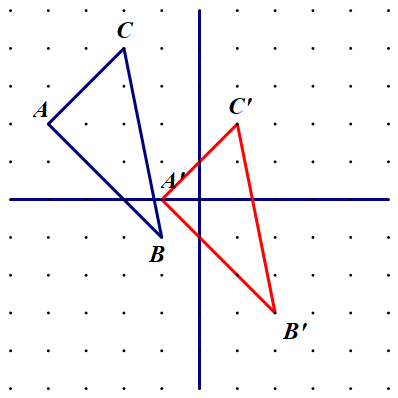
Je li trokut
dobiven translacijom trokuta
Ako je, odredite vektor translacije.
Je li rješenje jednoznačno? Objasnite.
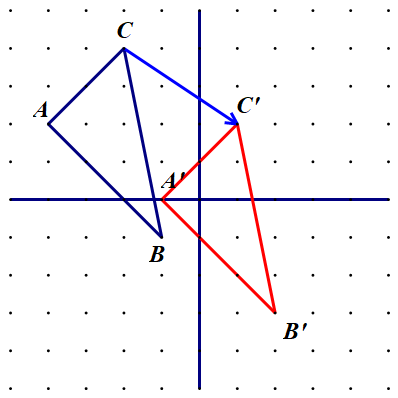
Rješenje je jednoznačno. Vektori
su jednaki vektori jer imaju isti smjer, istu orijentaciju i istu duljinu.
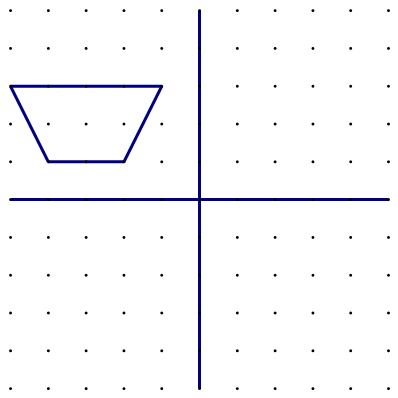
Odredite vektor koji će trapez preslikati iz drugog u četvrti kvadrant. Je li rješenje jednoznačno? Objasnite.

Neka je točka
s koordinatama
središte centralne simetrije. Na geoploči prikažite trokut tako da se cijeli trokut nalazi u prvom kvadrantu. Preslikajte trokut s obzirom na točku
kao centar simetrije. Usporedite trokut i njegovu centralnosimetričnu sliku. Što primjećujete?

Originalni trokut i njegova centralnosimetrična slika su sukladni. To znači da su im odgovarajuće stranice jednakih duljina te odgovarajući kutovi jednakih veličina.
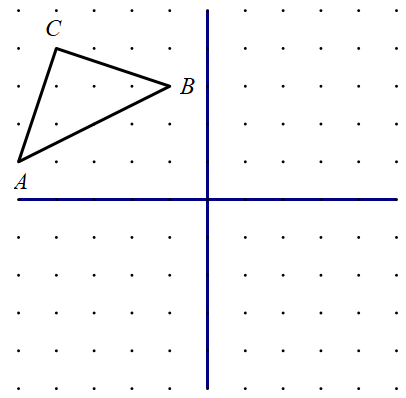
Centralnom simetrijom preslikajte prikazani trokut preko ishodišta kao osi simetrije. Ispišite koordinate vrhova trokuta i trokuta Što primjećujete?
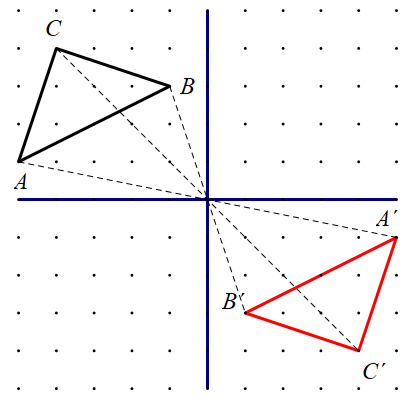
Koordinate vrhova trokuta
su
i
Koordinate vrhova trokuta
su
i
Centralnosimetrična slika točke s koordinatama s obzirom na ishodište koordinatnog sustava ima koordinate
Na geoploči prikažite trokut s vrhovima
i
Rotirajte trokut za
u pozitivnom smjeru oko ishodišta. Nacrtajte sliku i odredite koordinate dobivenih vrhova. Što primjećujete?
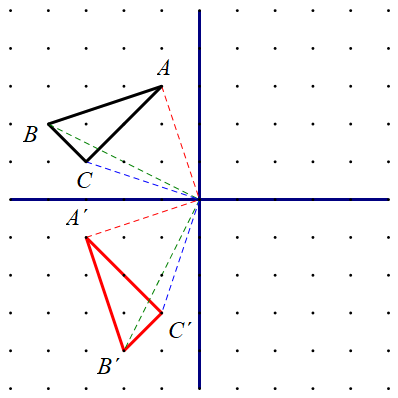
Koordinate vrhova trokuta
su
i
Koordinate vrhova trokuta
su
i
Slika točke s koordinatama rotirane za u pozitivnom smjeru oko ishodišta ima koordinate
Na geoploči prikažite trokut s vrhovima
i
Rotirajte trokut za
u negativnom smjeru oko ishodišta. Nacrtajte sliku i odredite koordinate dobivenih vrhova. Što primjećujete?
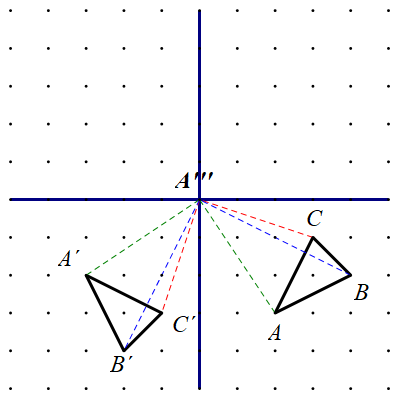
Koordinate vrhova trokuta su i
Koordinate vrhova trokuta su i
Slika točke s koordinatama rotirane za u negativnom smjeru oko ishodišta ima koordinate
Za kraj, možete „nacrtati“ nekoliko likova na geoploči koji su osnosimetrični, centralnosimetrični ili imaju rotacijsku simetriju te možete izraditi plakat ili prezentaciju u kojima ćete ih prikazati i detaljno opisati njihove simetrije.