Matematika 8 - 1.7 Razlika kvadrata

Razlika kvadrata

Izračunajmo sada umnožak zbroja i razlike dvaju racionalnih brojeva.

$(a + b) \cdot (a - b) = a^{2} + a b - b a - b^{2} = a^{2} - b^{2}$

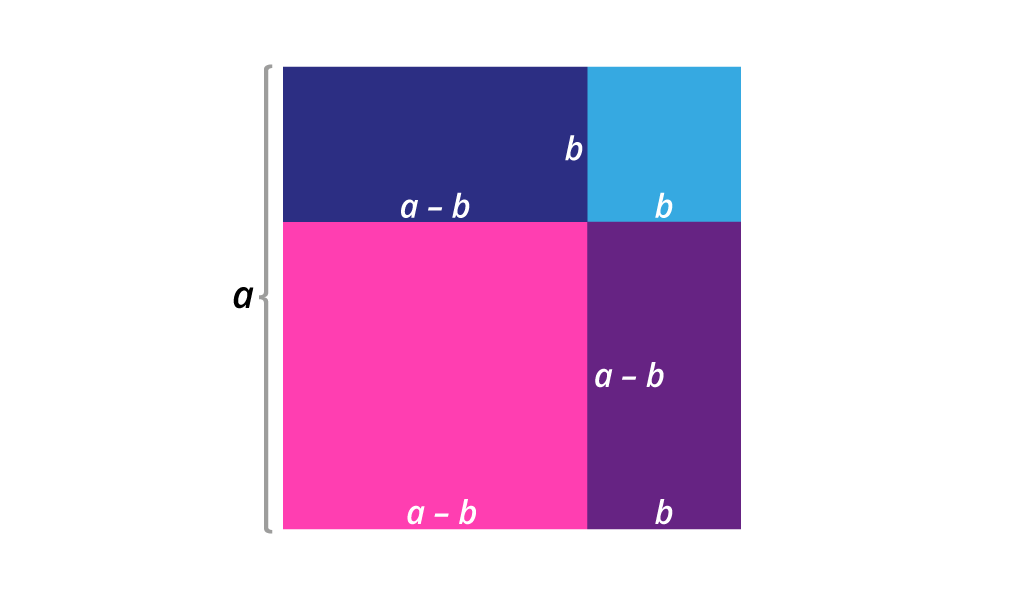
Ilustracija prikazuje tlocrt apartmana u obliku kvadrata. Kvadrat sa stranicom duljine a podijeljen je na dva kvadrata i dva pravokutnika.

Zbroj dvaju brojeva pomnožen njihovom razlikom daje razliku kvadrata tih brojeva pa možemo pisati:

$(a + b) \cdot (a - b) = a^{2} - b^{2}$

Dakle, razlika kvadrata dvaju racionalnih brojeva jednaka je umnošku zbroja i razlike tih brojeva. Ako razliku kvadrata dvaju brojeva $a^{2} - b^{2}$ napišemo u obliku umnoška $(a + b) \cdot (a - b),$ kažemo da smo razliku kvadrata rastavili na faktore. Pišemo:

$a^{2} - b^{2} = (a + b) \cdot (a - b)$

Tu formulu, radi lakšeg pamćenja, možemo izreći i ovako:

${prvi}^{2} - {drugi}^{2} = (prvi+drugi) \cdot (prvi - drugi)$

Primijenimo sada tu formulu na nekoliko primjera.

Formulu možemo upotrijebiti za množenje zbroja i razlike dvaju brojeva.

Primjer 1.

Na papir napišimo u obliku razlike kvadrata sljedeće umnoške.

$(a + 5) \cdot (a - 5)$

$(4 - 3 c) \cdot (4 + 3 c)$

$(0.2 x - 0.3 y) \cdot (0.2 x + 0.3 y)$

$(a + 5) \cdot (a - 5) = a^{2} - 5^{2} = a^{2} - 25$
$(4 - 3 c) \cdot (4 + 3 c) = 4^{2} - (3 c)^{2} = 16 - 9 c^{2}$
$(0.2 x - 0.3 y) \cdot (0.2 x + 0.3 y) = {(0.2 x)}^{2} - {(0.3 y)}^{2} = 0.04 x^{2} - 0.09 y^{2}$

… ili za rastavljanje razlike kvadrata dvaju brojeva na faktore.

Primjer 2.

Rastavimo razliku kvadrata na faktore.

$x^{2} - 36$

$\frac{9}{16} y^{2} - \frac{25}{36} z^{2}$

$x^{2} - 36 = x^{2} - 6^{2} = (x - 6) \cdot (x + 6)$
$\frac{9}{16} y^{2} - \frac{25}{36} z^{2} = (\frac{3}{4} y)^{2} - (\frac{5}{6} z)^{2} = (\frac{3}{4} y + \frac{5}{6} z) \cdot (\frac{3}{4} y - \frac{5}{6} z)$

Primjer 3.

Primijenimo formulu za razliku kvadrata i izračunajmo.

$75 \cdot 125$

$75 \cdot 125 = (100 - 25) (100 + 25) = 100^{2} - 25^{2} = 10 000 - 625 = 9 375$

Riješite zadatke koristeći se algebarskim pločicama.

Prisjetite se da crvene pločice možete dobiti pritiskom na bilo koju od postojećih pločica. Na isti način i vraćate polaznu boju pločice.

Kolekcija zadataka 1

Zadatak 1.

Napiši na papir umnoške u obliku razlike kvadrata.

$(3 a + b) (3 a - b)$
$(2 x - 3) (2 x + 3)$
$(1 + 6 y) (1 - 6 y)$
$(4 - 5 a) (4 + 5 a)$
$(\frac{1}{7} x + \frac{2}{9} y) (\frac{1}{7} x - \frac{2}{9} y)$
$(0.4 c - 0.6 d) (0.4 c + 0.6 d)$

$\begin{array}{l} (3 a + b) (3 a - b) = 9 a^{2} - b^{2} \end{array}$
$\begin{array}{l} (2 x - 3) (2 x + 3) = 4 x^{2} - 9 \end{array}$
$\begin{array}{l} (1 + 6 y) (1 - 6 y) = 1 - 36 y ² \end{array}$
$(4 - 5 a) (4 + 5 a) = 16 - 25 a^{2}$
$\begin{array}{l} (\frac{1}{7} x + \frac{2}{9} y) (\frac{1}{7} x - \frac{2}{9} y) = \frac{1}{49} x^{2} - \frac{4}{81} y^{2} \end{array}$
$\begin{array}{l} (0.4 c - 0.6 d) (0.4 c + 0.6 d) = 0.16 c^{2} - 0.36 d^{2} \end{array}$

Zadatak 2.

Rastavi razliku kvadrata na faktore.

$16 x^{2} - 25 y^{2}$
$\frac{1}{4} a^{2} - \frac{9}{49} b^{2}$
$0.25 x^{2} - 0.81 y^{2}$
$121 p^{2} - 144 r^{2}$

$16 x^{2} - 25 y^{2} = (4x - 5y) (4x + 5y)$
$\frac{1}{4} a^{2} - \frac{9}{49} b^{2} = (\frac{1}{2} a - \frac{3}{7} b) (\frac{1}{2} a + \frac{3}{7} b)$
$0.25 x^{2} - 0.81 y^{2}$ $= (0.5 x + 0.9 y) (0.5 x - 0.9 y)$
$121 p^{2} - 144 r^{2} = 11 p + 12 r 11 p - 12 r$

Zadatak 3.

Prepišite jednakosti na papir i dopuni te ih tako da jednakosti budu istinite.

$49 x^{2} - 100 y^{2} = (__-___) \cdot (7 x + 10 y)$
$___c^{2} - 16 d^{2} = (3 c - 4 d) \cdot (3 c +___)$
$0.0121 -____s^{2} = (_____+ 0.02 s) \cdot (______- 0.02 s)$

$49 x^{2} - 100 y^{2} = (7 x - 10 y) \cdot (7 x + 10 y)$
$9 c^{2} - 16 d^{2} = (3 c - 4 d) \cdot (3 c + 4 d)$
$0.0121 - 0.0004 s^{2} = (0.11 + 0.02 s) \cdot (0.11 - 0.02 s)$

Zatvori

Kolekcija zadataka 2

Zadatak 4.

Primijeni formulu za razliku kvadrata i izračunaj.

$95 \cdot 105$
$30.3 \cdot 9.7$
$891 \cdot 909$

$95 \cdot 105 = (100 - 5) (100 + 5) = 100^{2} - 5^{2} = 10 000 - 25 = 9 975$
$10.3 \cdot 9.7 = (10 + 0.3) (10 - 0.3) = 10^{2} - {0.3}^{2} = 100 - 0.09 = 99.91$
$891 \cdot 909 = (900 - 9) (900 + 9) = 900^{2} - 9^{2} = 8 100 - 81 = 8 019$

Zadatak 5.

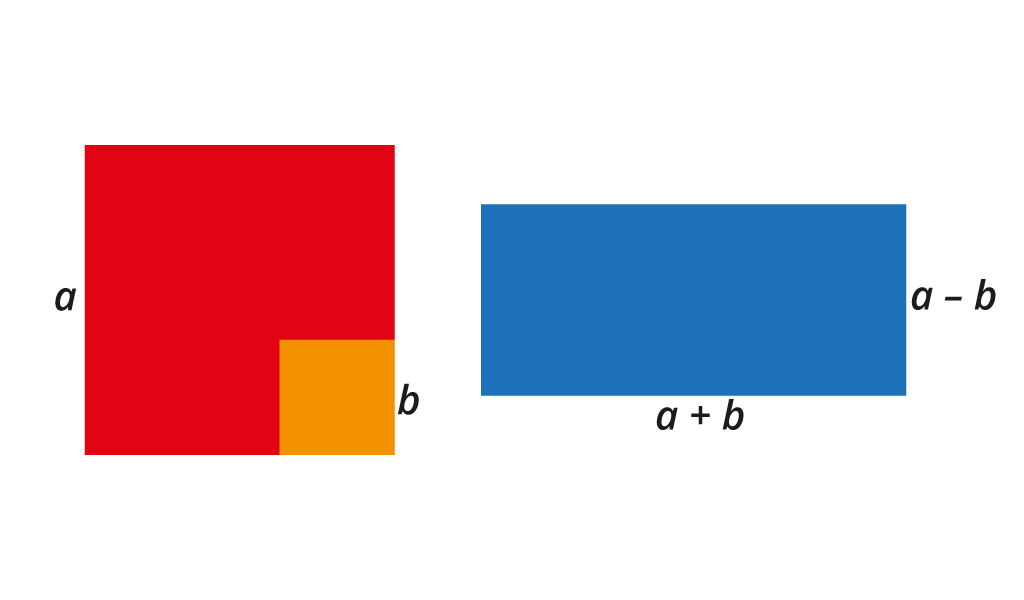
Na slici se nalaze kvadrat i pravokutnik. Kvadrat ima duljinu stranice a cm i unutar njega u donjem desnom kutu kvadrat duljine b cm. Potrebno je izračunati razliku površina tih dvaju kvadrata. Pravokutnik ima duljine stranica (a+b) cm i (a-b) cm.

Usporedi površine crvenoga i plavoga geometrijskog lika sa slike.

Procijeni koji od njih ima veću površinu?

Provjeri rješenje za $a = 5 cm$ i $b = 2 cm .$

Površina je većeg kvadrata jednaka $a^{2},$ a površina je manjeg kvadrata jednaka $b^{2} .$ Razlika površina tih dvaju kvadrata jednaka je površini crvenoga geometrijskog lika $a^{2} - b^{2} = (a + b) \cdot (a - b) .$

Površina je pravokutnika jednaka $(\begin{array}{l} a + b \end{array}) \cdot (\begin{array}{l} a - b \end{array}) = a^{2} - b^{2}$ .

Dakle, zadane su površine jednake.

Za $a = 5 cm$ i $b = 2 cm$ površina je većeg kvadrata jednaka $5^{2} = 25 {cm}^{2},$ a površina je manjeg kvadrata jednaka $2^{2} = 4 {cm}^{2} .$ Razlika je tih dviju površina $21 {cm}^{2} .$

Za $a = 5 cm$ i $b = 2 cm$ površina je pravokutnika jednaka $7 \cdot 3 = 21 {cm}^{2} .$

Zadatak 6.

Obitelji Mudrić ponuđena je radi izgradnje autoceste zamjena poljoprivrednog zemljišta. Za njihovo im je zemljište u obliku kvadrata ponuđeno zemljište u obliku pravokutnika. Jedna je stranica novog zemljišta $12 m$ dulja, a druga $12 m$ kraća od stranice njihova zemljišta. Isplati li se obitelji Mudrić zamjena zemljišta?

Objasnite odgovor.

Na slici je prikaz kvadratnog poljoprivrednog zemljišta sa stranicom duljine x m i slika pravokutnog poljoprivrednog zemljišta kojemu su duljine stranica x+12 m,x-12 m.

Površina zemljišta u obliku kvadrata sa stranicom duljine $x m$ jednaka je $x^{2} .$ Površina je zemljišta u obliku pravokutnika jednaka $(x + 12) (x - 12) = x^{2} - 144 .$ Obitelji Mudrić se ne isplati zamjena zemljišta jer je nova površina za $144 m^{2}$ manja od površine zemljišta koje imaju u vlasništvu.

Zatvori

Kolekcija zadataka 3

Zadatak 7.

Lucijin je suprug promijenio dimenzije gredice s jagodama u vrtu. Gredicu u obliku kvadrata duljine stranica $x$ skratio je za $3 m$ po širini i produljio za $3 m$ po dužini. Lucija je nezadovoljna novom veličinom gredice s jagodama. Zašto? Usporedi površine nove i stare gredice.

Površina kvadratne gredice sa stranicom duljine $x m$ jednaka je $x^{2} .$ Površina gredice u obliku pravokutnika jednaka je $(x + 3) (x - 3) = x^{2} - 9 .$ Lucija je s pravom nezadovoljna jer je površina nove gredice za $9 m^{2}$ manja od početne površine gredice.

Dovuci odgovarajuće algebarske izraze na njihove jednakosti.

$(\frac{1}{2} - c) (\frac{1}{2} + c)$	$\frac{1}{4} - c^{2}$
${(\frac{1}{2} - c)}^{2}$	$(\frac{1}{2} - c) (\frac{1}{2} - c)$
${(c + \frac{1}{2})}^{2}$	$(c + \frac{1}{2}) (c + \frac{1}{2})$
$(\frac{1}{2} + c) (c - \frac{1}{2})$	$c^{2} - \frac{1}{4}$

null

Dovuci odgovarajuće algebarske izraze na njihove jednakosti.

$0.04 - 49 x^{2}$	$(7 x + 0.2) (7 x + 0.2)$
$49 x^{2} + 2.8 x + 0.04$	$(0.2 - 7 x) (0.2 + 7 x)$
$49 x^{2} - 0.04$	$(0.2 + 7 x) (7 x - 0.2)$
$49 x^{2} - 2.8 x + 0.04$	$(7 x - 0.2) (7 x - 0.2)$

null

Dovuci izraze na odgovarajuća mjesta.
$(x + 7) \cdot (7 - x) =$

.
$(x - 7) \cdot (x + 7) =$

.
$(4 + a) \cdot (a - 4) =$

.
$(4 - a) \cdot (4 + a) =$

.

$49 - x^{2}$

$16 - a^{2}$

$x^{2} - 49$

$a^{2} - 16$

null

null

Zadatak 8.

Opsezi dvaju kvadrata razlikuju se za $16 cm$ , a njihove površine za $72 {cm}^{2} .$ Kolike su duljine stranica tih kvadrata?

$O_{2} - O_{1} = 16 cm$

$P_{2} - P_{1} = 72 {cm}^{2}$

$4 (a_{2} - a_{1}) = 16$ $/ : 4$ $→$ $a_{2} - a_{1} = 4$

$a_{2}^{2} - a_{1}^{2} = 72$ $a_{2}^{2} - a_{1}^{2}$ $= (a_{2} - a_{1}) (a_{2} + a_{1}) = 72$

$4 (a_{2} + a_{1}) = 72$ $/ : 4$ $\to$ $a_{2} + a_{1} = 18$

$a_{2} - a_{1} = 4,$ $a_{2} + a_{1} = 18$

Rješavanjem ovog sustava dviju linearnih jednadžbi s dvjema nepoznanicama dobivamo da je $a_{2} = 11 cm$ i $a_{1} = 7 cm .$ Duljine stranica tih kvadrata imaju duljine $11 cm$ i $7 cm .$

Zadatak 9.

Površinu pravokutnika možemo izraziti s pomoću formule $P = a \cdot b .$ Kolike mogu biti duljine stranica da bismo dobili površinu $36 a b ?$ Ispiši na papir sve mogućnosti uz uvjet da su $a$ i $b$ prirodni brojevi.

$a$	$1 a$	$2 a$	$3 a$	$4 a$	$6 a$	$9 a$	$12 a$	$18 a$	$36 a$
$b$	$36 b$	$18 b$	$12 b$	$9 b$	$6 b$	$4 b$	$3 b$	$2 b$	$1 b$
$P$	$36 a b$	$36 a b$	$36 a b$	$36 a b$	$36 a b$	$36 a b$	$36 a b$	$36 a b$	$36 a b$

Sve mogućnosti za rješenje zadatka dane su u tablici.

Zatvori

U sljedećem videu dokazat ćemo tvrdnju: Ako oduzmemo kvadrate dvaju uzastopnih prirodnih brojeva, dobit ćemo isti rezultat kao da smo zbrojili ta dva prirodna broja. Pogledajmo video!

1.7 Razlika kvadrata

Na početku...

Razlika kvadrata

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zadatak 3.

Kolekcija zadataka 2

Zadatak 4.

Zadatak 5.

Zadatak 6.

Kolekcija zadataka 3

Zadatak 7.

Zadatak 8.

Zadatak 9.

...i na kraju