Matematika 8 - 2.5 Zbrajanje i oduzimanje potencija s bazom 10

Zbrajanje i oduzimanje potencija s bazom $10$

Zanimljivost

Rhindov papirus jedan je od najstarijih sačuvanih matematičkih rukopisa. Zapisao ga je staroegipatski pisar Ahmes te se stoga često naziva i Ahmesov papirus.

Naziv Rhindov papirus dobio je po egiptologu Alexanderu Henryju Rhindu koji ga je kupio u Luxoru 1858. godine. Sadrži $87$ matematičkih problema i prikaz je matematičkog znanja starih Egipćana. Iz njega je vidljivo da su stari Egipćani znali dijeliti i množiti, računati s razlomcima te rješavati probleme iz geometrije, kao što su problemi vezani za površine i volumene. Zanimljivo je da je približna vrijednost broja $π$ u tome dokumentu $3.16 .$

Danas se Rhindov papirus čuva u Britanskom muzeju u Londonu.

Na fotografiji je prikaz Rhindova papirusa. — Rhindov papirus

Jedan od zadataka zapisanog u Rhindovu papirusu iz 1650. godine prije nove ere glasi: U svakoj je od sedam kuća sedam mačaka, svaka mačka uhvati po sedam miševa od kojih bi svaki pojeo po sedam klasova žita, iz svakog bi klasa niklo sedam mjerica zrnja. Cilj je zadatka odrediti koliko je ukupno toga opisano tekstom zadatka.

$7 + 7^{2} + 7^{3} + 7^{4} + 7^{5} = 7 + 49 + 343 + 2 401 + 16 807 = 19 607$

Zadatak 5.

Preoblikujmo zadatak u sljedeći: U svakoj je od deset kuća deset mačaka koje uhvate po deset miševa od kojih svaki jede deset zrna pšenice, a svako zrno daje deset mjerica žita. Koliko je ukupno životinja/stvari opisano u zadatku?

$10 + 10^{2} + 10^{3} + 10^{4} + 10^{5} = 10 + 100 + 1 000 + 10 000 + 100 000 = 111 110$

Kao što vidimo, ponekad je potrebno zbrojiti i/ili oduzeti potencije. No, moramo li uvijek brojeve zapisati u dekadskom zapisu pa ih onda zbrojiti? Istražimo.

Povezani sadržaji

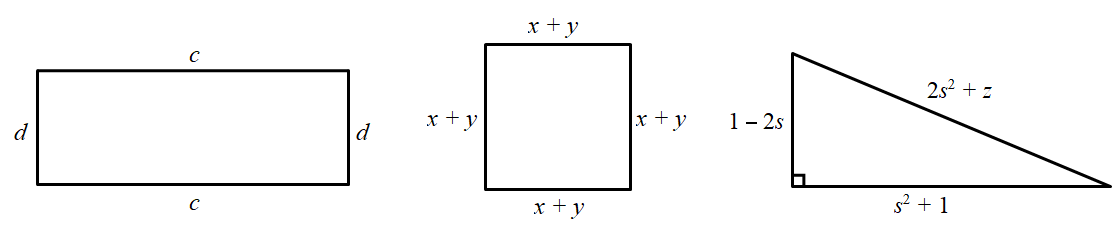
Napišite u bilježnicu formulu za opseg geometrijskog lika uz oznake na slici. Prisjetite se, opseg geometrijskog lika jednak je zbroju duljina svih stranica koje ga omeđuju.

Na slici su geometrijski likovi s istaknutim duljinama stranica.

$o_{1} = c + d + c + d = 2 c + 2 d$

$o_{2} = (x + y) + (x + y) + (x + y) + (x + y) = 4 x + 4 y$

$o_{3} = 1 - 2 s + s^{2} + 1 + 2 s^{2} + z = 3 s^{2} - 2 s + z + 2$

Povezani sadržaji

Željko kupuje poklone za svojih $10$ prijatelja. Odlučio je da će nekima kupiti CD, a nekima knjigu. Cijena knjiga koje želi kupiti iznosi $80 kn$ po komadu, a CD-a $75 kn$ po komadu. Napiši u bilježnicu izraz za ukupan iznos koji Željko treba potrošiti na poklone u ovisnosti o broju kupljenih knjiga. Odredite iznos koji treba platiti ako kupi $6$ knjiga.

Neka $n$ predstavlja broj kupljenih knjiga. Tada $10 - n$ predstavlja broj kupljenih CD-a.

S obzirom na to da je cijena knjige $80 kn$ po komadu, knjige će ukupno platiti $80 n$ kuna. Cijena CD-a po komadu iznosi $75$ kuna te će CD-e ukupno platiti $75 (10 - n) kn .$

Dakle, ukupno će platiti $80 n + 75 (10 - n)$ tj. $80 n + 750 - 75 n = 5 n + 750 kn .$

Ako kupi $6$ knjiga, ukupno će platiti $5 \cdot 6 + 750 = 780 kn .$

Uočite! Odgovarajući se članovi (istoimeni članovi npr. $3$ i $- 5$ ; $2 x$ i $7 x$ ; $4 y^{3} i - y^{3}$ ) uvijek mogu zbrojiti i oduzeti te se na taj način pojednostavljuje algebarski izraz.

Npr. $7 + 5 z + 11 z = 7 + (5 + 11) z = 7 + 16 z$

Kolekcija zadataka 2

Zadatak 6.

Spojite članove na njihove odgovarajuće (istoimene) članove.

$3 \cdot 2^{8}$	$- 8 a$
$- x y^{2}$	$5 d^{3}$
$6 a$	$- 2 \cdot 10^{7}$
$5 \cdot 10^{7}$	$3 y^{2} x$
$11 d^{3}$	$- 7 \cdot 2^{8}$

null

Zadatak 7.

Osmi razred neke škole za kraj školske godine naručuje razredne majice. Cijena bijele majice s tiskom iznosi $30 kn,$ a crvene $45 kn .$ Napišite u bilježnicu izraz za ukupan iznos koji razredni odjel od $24$ učenika treba platiti za majice u ovisnosti o broju bijelih majica.

Neka $b$ predstavlja broj bijelih majica. Tada broj crvenih majica iznosi $24 - b .$

Ukupan iznos koji treba platiti tada iznosi:

$30 b + 45 (24 - b) = 30 b + 1 080 - 45 b = 1 080 - 15 b .$

Zatvori

Baš kao što ste u prethodnim zadatcima zbrajali i/ili oduzimali samo odgovarajuće članove, tako ćemo pri radu s potencijama zbrajati i/ili oduzimati samo potencije koje imaju jednake baze i jednake eksponente. Baza naših potencija bit će broj $10 .$

Primjer 1.

Izlučimo zajednički faktor i izračunajmo.

$2 \cdot 10^{3} + 5 \cdot 10^{3}$

$5 \cdot 10^{4} - 6 \cdot 10^{4}$

$4 \cdot 10^{- 2} + 3 \cdot 10^{- 2}$

$2 \cdot 10^{3} + 5 \cdot 10^{3} = (2 + 5) \cdot 10^{3} = 7 \cdot 10^{3} .$

Rezultat provjerimo.

$2 \cdot 10^{3} + 5 \cdot 10^{3} = 2 000 + 5 000 = 7 000 = 7 \cdot 10^{3}$
$5 \cdot 10^{4} - 6 \cdot 10^{4} = (5 - 6) \cdot 10^{4} = - 1 \cdot 10^{4}$

Rezultat provjerimo.

$5 \cdot 10^{4} - 6 \cdot 10^{4} = 50 000 - 60 000 = - 10 000 = - 1 \cdot 10^{4}$
$4 \cdot 10^{- 2} + 3 \cdot 10^{- 2} = (4 + 3) \cdot 10^{- 2} = 7 \cdot 10^{- 2}$

Rezultat provjerimo.

$4 \cdot 10^{- 2} + 3 \cdot 10^{- 2} = 0.04 + 0.03 = 0.07 = 7 \cdot 10^{- 2}$

Zbrajati i oduzimati mogu se samo potencije koje imaju jednake baze i jednake eksponente. Potencije jednakih baza i jednakih eksponenata zbrajamo i oduzimamo tako da im zbrojimo/oduzmemo njihove koeficijente te rezultat pomnožimo zajedničkom potencijom.

$a \cdot 10^{n} + b \cdot 10^{n} = (a + b) \cdot 10^{n},$ za $n,$ $a,$ $b \in N$
$a \cdot 10^{n} - b \cdot 10^{n} = (a - b) \cdot 10^{n},$ za $n \in N,$ $a,$ $b \in Z$

Kolekcija zadataka 3

Zadatak 8.

Izlučite zajednički faktor pa izračunajte $2 \cdot 10^{5} + 3 \cdot 10^{5} + 4 \cdot 10^{5} .$

$2 \cdot 10^{5} + 3 \cdot 10^{5} + 4 \cdot 10^{5} = (2 + 3 + 4) \cdot 10^{5} = 9 \cdot 10^{5}$

Zadatak 9.

Izračunajte $- 3 \cdot 10^{8} + 2 \cdot 10^{8} .$

$- 3 \cdot 10^{8} + 2 \cdot 10^{8} = (- 3 + 2) \cdot 10^{8} = - 1 \cdot 10^{8} = - 10^{8}$

Prisjetite se.

$\begin{array}{l} 1 \cdot 10^{n} = 10^{n} \\ - 1 \cdot 10^{n} = - 10^{n} \end{array}$

Zadatak 10.

Izračunajte $10^{- 6} - 3 \cdot 10^{- 6} .$

$10^{- 6} - 3 \cdot 10^{- 6} = - 2 \cdot 10^{- 6}$

Zatvori

Kolekcija zadataka 4

Zadatak 11.

Dovucite zadatak na njegovo odgovarajuće rješenje.

$10^{4} + 10^{4}$	$10^{8}$
$9 \cdot 10^{7} + 10^{7}$	$- 2 \cdot 10^{- 2}$
$5 \cdot 10^{8} - 7 \cdot 10^{8}$	$10^{4}$
$- 10^{- 2} - 10^{- 2}$	$2 \cdot 10^{4}$
$7 \cdot 10^{3} + 3 \cdot 10^{3}$	$- 2 \cdot 10^{8}$

null

Zadatak 12.

Na slici se nalazi bilježnica s evidencijom neizvršavanja obaveza pranja posuđa za veljaču

Studenti Mateja, Tomica i Karlo zajednički iznajmljuju stan i dijele zaduženja oko pospremanja. No, ponekad svoje obveze ne izvršavaju kako treba. Najveći im problem predstavlja pranje posuđa. Stoga su odlučili da će na kraju mjeseca svaki od njih u zajedničku kasicu za kupnju namirnica ubaciti $10^{n}$ lipa gdje $n$ predstavlja broj dana u mjesecu kada netko od njih nije oprao posuđe na dan kada je bio njegov red.

Na kraju veljače pogledali su evidenciju neizvršenih obveza pranja posuđa. Koliko novca u kasicu treba ubaciti svaki od njih? Koliko su ukupno novca ubacili u kasicu?
Nakon koliko bi puta netko u kasicu trebao ubaciti $1 000 kn ?$
Koliko bi trebao platiti netko tko nije suđe oprao $10$ dana?
Nakon godine dana Mateja je pogledala zabilješke u bilježnici.
- Sedam je puta morala ubaciti novac u kasicu jer $2$ puta u istom mjesecu nije oprala posuđe.
- Četiri je puta morala ubaciti novac u kasicu jer jedanput u istom mjesecu nije oprala posuđe.
- Jedanput je morala u kasicu ubaciti novac jer $3$ puta u istom mjesecu nije oprala posuđe.
Koliko je ukupno te godine ubacila u kasicu?

Mateja je u kasicu ubacila $10^{3}$ lipa, Tomica $10^{2}$ lipa, a Karlo $10^{4}$ lipa, tj. Mateja je ubacila $1 000 lp = 10 kn,$ Tomica $100 lp,$ tj. $1 kn,$ a Karlo $10 000 lp,$ tj. $100 kn .$ Dakle, ukupno su u kasicu stavili $10 + 4 + 100 = 114 kn .$
$1 000 kn$ je $100 000 lp .$ $100 000 = 10^{5}$ tj. $n = 5 .$ Nakon što netko toga mjeseca $5$ puta ne izvrši svoje zaduženje pranja posuđa, morao bi u kasicu ubaciti $1 000 kn .$
Kad netko ne bi posuđe oprao $10$ dana trebao bi u kasicu ubaciti $10^{10} = 10 000 000 000 lp = 100 000 000 kn!$
Ukupno je u kasicu ubacila $7 \cdot 10^{2} + 4 \cdot 10^{1} + 10^{3} kn .$ U ovome su zadatku potencije broja $10$ različite te zadatak znamo riješiti isključivo pretvaranjem u dekadski zapis.

$7 \cdot 10^{2} + 4 \cdot 10^{1} + 10^{3} = 700 + 40 + 1 000 = 1 740 kn$

Mateja je tijekom godine u kasicu ubacila ukupno $1 740 kn .$

Zatvori

Kao što ste vidjeli u prethodnom zadatku, ponekad je potrebno zbrojiti/oduzeti brojeve zapisane potencijama broja $10$ koje nemaju iste eksponente. Takvi se brojevi uvijek mogu zapisati u svojim dekadskim ili decimalnim zapisima te onda zbrojiti/oduzeti, ali taj postupak nije uvijek brz i učinkovit.

Povezani sadržaji

U petome ste razredu u cjelini Prirodni brojevi proučavali mjesne vrijednosti. Promotrite kako su mjesne vrijednosti povezane s potencijama broja $10 .$

Na slici su prikazane mjesne vrijednosti broja.

$123 456.789 = 1 \cdot 10^{5} + 2 \cdot 10^{4} + 3 \cdot 10^{3} + 4 \cdot 10^{2} + 5 \cdot 10^{1} + 6 \cdot 10^{0} + 7 \cdot 10^{- 1} + 8 \cdot 10^{- 2} + 9 \cdot 10^{- 3}$

Primjer 2.

Izračunajmo $3 \cdot 10^{2} + 5 \cdot 10^{1} + 6 \cdot 10^{0} + 4 \cdot 10^{- 1}$

$3 \cdot 10^{2} + 5 \cdot 10^{1} + 6 \cdot 10^{0} + 4 \cdot 10^{- 1} = 300 + 50 + 6 + 0.4 = 356.4$

No ponekad je jednostavnije ne pretvarati brojeve u dekadski/decimalni zapis, već samo izlučiti zajedničku potenciju broja $10 .$

Primjer 3.

Izlučimo zajednički faktor pa izračunajmo:

$- 7 \cdot 10^{6} + 4 \cdot 10^{5}$

$9 \cdot 10^{7} - 7 \cdot 10^{5}$

$- 7 \cdot 10^{6} + 4 \cdot 10^{5} = - 7 \cdot 10 \cdot 10^{5} + 4 \cdot 10^{5} = (- 70 + 4) \cdot 10^{5} = - 66 \cdot 10^{5}$

Rezultat provjerimo pretvaranjem brojeva u dekadski zapis i zbrajanjem/oduzimanjem brojeva u dekadskom zapisu.

$- 7 \cdot 10^{6} + 4 \cdot 10^{5} = - 7 000 000 + 400 000 = - 6 600 000 = - 66 \cdot 10^{5}$
$9 \cdot 10^{7} - 7 \cdot 10^{5} = 9 \cdot 10^{2} \cdot 10^{5} - 7 \cdot 10^{5} = (900 - 7) \cdot 10^{5} = 893 \cdot 10^{5}$

Zadatak 13.

Izračunajte $3 \cdot 10^{2} + 5 \cdot 10^{4}$

Rješenje provjerite tako da brojeve zapišete, u bilježnicu, u dekadskom zapisu te zbrojite.

$3 \cdot 10^{2} + 5 \cdot 10^{4} = 3 \cdot 10^{2} + 5 \cdot 10^{2} \cdot 10^{2} = (3 + 500) \cdot 10^{2} = 503 \cdot 10^{2}$

Provjera:

$3 \cdot 10^{2} + 5 \cdot 10^{4} = 300 + 50 000 = 50 300 = 503 \cdot 10^{2}$

Brojeve zapisane pomoću potencija broja $10$ s različitim eksponentima zbrajamo/oduzimamo tako da ih izrazimo pomoću potencija s istim eksponentom, a zatim zbrojimo/oduzmemo njihove koeficijente.

$a \cdot 10^{n} + b \cdot 10^{m} = (a \cdot 10^{n - m} + b) \cdot 10^{m}$
$a \cdot 10^{n} - b \cdot 10^{m} = (a \cdot 10^{n - m} - b) \cdot 10^{m}$

$m, n \in N, a, b \in Z, n > m$

Kolekcija zadataka 5

Zadatak 14.

Zadatak zapišite u bilježnicu pomoću potencija broja $10$ s istim eksponentom, izlučite zajednički faktor pa izračunajte. Rješenje provjerite tako da brojeve zapišete u decimalnom zapisu te ih oduzmete.

$7 \cdot 10^{- 3} - 2 \cdot 10^{- 4}$

$7 \cdot 10^{- 3} - 2 \cdot 10^{- 4} = 70 \cdot 10^{- 4} - 2 \cdot 10^{- 4} = (70 - 2) \cdot 10^{- 4} = 68 \cdot 10^{- 4} = 6.8 \cdot 10^{- 3}$

Provjera:

$7 \cdot 10^{- 3} - 2 \cdot 10^{- 4} = 0.007 - 0.0002 = 0.0068 = 6.8 \cdot 10^{- 3}$

Zadatak 15.

Izračunajte: $4 \cdot 10^{9} - 2 \cdot (10^{8} - 6 \cdot 10^{8}) .$

$4 \cdot 10^{9} - 2 \cdot (10^{8} - 6 \cdot 10^{8}) = 4 \cdot 10^{9} - 2 \cdot 10^{8} + 12 \cdot 10^{8} = 4 \cdot 10^{9} + 10 \cdot 10^{8} = 4 \cdot 10^{9} + 10^{9} = 5 \cdot 10^{9}$

Zatvori

$6 \cdot 10^{7} + 7 \cdot 10^{7} - 5 \cdot 10^{7}$	$8 \cdot 10^{7}$
$(32 \cdot 10^{2}) : (8 \cdot 10^{- 4}) \cdot (2 \cdot 10^{12})$	$8 \cdot 10^{18}$
$(4 \cdot 10^{7})^{2}$	$16 \cdot 10^{14}$

2.5 Zbrajanje i oduzimanje potencija s bazom 10

Na početku...

Brojevi, brojevi, brojevi

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zadatak 3.

Zadatak 4.

Zbrajanje i oduzimanje potencija s bazom $10$

Zanimljivost

Zadatak 5.

Povezani sadržaji

Povezani sadržaji

Kolekcija zadataka 2

Zadatak 6.

Zadatak 7.

Kolekcija zadataka 3

Zadatak 8.

Zadatak 9.

Zadatak 10.

Kolekcija zadataka 4

Zadatak 11.

Zadatak 12.

Povezani sadržaji

Zadatak 13.

Kolekcija zadataka 5

Zadatak 14.

Zadatak 15.

...i na kraju

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

2.6 Znanstveni zapis broja