

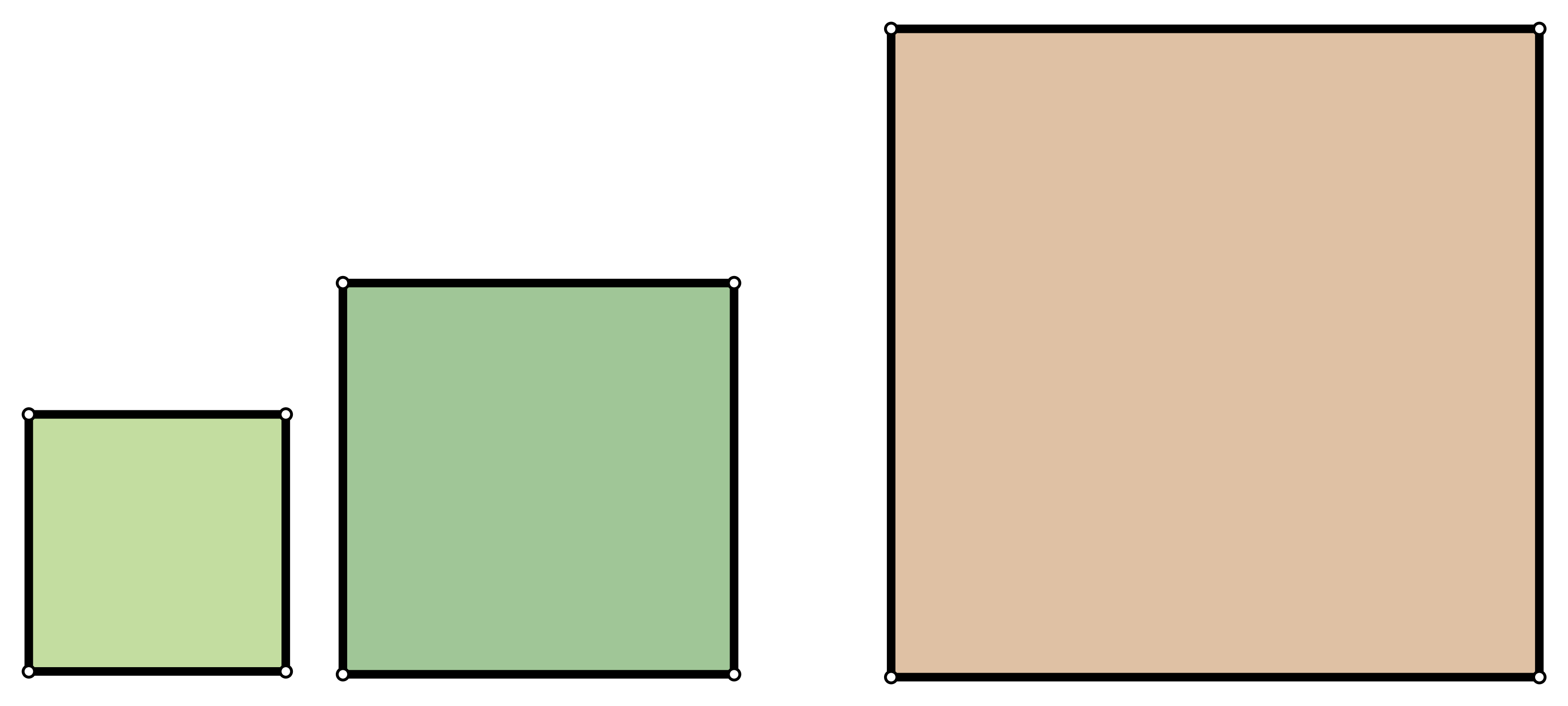
Susjed Stipe ima dva zemljišta u obliku kvadrata. Prvo zemljište ima opseg a drugo Stipe želi ta dva zemljišta zamijeniti za treće, koje je također u obliku kvadrata. Kolika treba biti duljina „zamjenskog” zemljišta ako Stipe želi da to zemljište ima:
Ukupan je opseg ovih dvaju zemljišta metara.
Označimo li s duljinu stranice „zamjenskog” kvadrata, njegov opseg računamo prema formuli Zato vrijedi jednadžba pa je odnosno Duljina bi „zamjenskog” zemljišta trebala biti metara.
Duljina je prvog zemljišta metra pa je njegova površina jednaka kvadratnih metara. Duljina je drugog zemljišta metra pa je njegova površina jednaka kvadratnih metara.
Ukupna je površina tih dvaju zemljišta kvadratnih metara.
Označimo li s duljinu stranice „zamjenskog” kvadrata, njegovu površinu računamo prema formuli Zato vrijedi jednadžba pa je tj. Duljina bi „zamjenskog” zemljišta trebala biti metara.
Četvorni hvat (znak čhv) zastarjela je mjerna jedinica za površinu, službeno napuštena uvođenjem Metarskog sustava. U austrijskom dijelu Austro-Ugarske podatci su u katastarskim knjigama pretvoreni u metarske jedinice još 1873. god. U ugarskome dijelu te promjene nisu učinjene pa se u hrvatskim zemljišnim knjigama četvorni hvat rabio još stotinjak godina poslije, većinom skraćeno nazivan samo hvat. Vrijednost četvornog hvata je kvadrat bečkog hvata (mjerna jedinica za duljinu od
), pa je
ili
Rješavajući uvodni zadatak, rješavali smo jednadžbe.
Jednadžba spada u skupinu dobro vam poznatih, linearnih jednadžbi.
Jednadžba izgleda drukčije. U njoj se javlja nepoznanica pomnožena sa samom sobom, dakle kvadrirana. Jednadžbu takvog oblika nazivamo kvadratnom jednadžbom.
Prisjetimo se!
Neka su , i racionalni brojevi, pri čemu je
Jednadžbu oblika nazvali smo linearnom jednadžbom s (jednom) nepoznanicom .
Rješenje je linearne jednadžbe oblika onaj racionalni broj koji, uvrštavanjem u jednadžbu, daje istinitu brojevnu jednakost.
Dvije su jednadžbe ekvivalentne ako imaju isto rješenje.
U svijetu oko nas brojne zakonitosti nisu povezane linearnom nego kvadratnom vezom. Takve su zakonitosti, primjerice, kinetička energija i slobodni pad (jednoliko ubrzano gibanje). Pri rješavanju takvih zadataka potrebno je rješavati jednadžbe oblika:
Neka su , i racionalni brojevi, pri čemu je Jednadžbu koju je moguće napisati u obliku nazvat ćemo kvadratnom jednadžbom s (jednom) nepoznanicom .
Rješenje kvadratne jednadžbe oblika
je onaj racionalni broj
koji uvrštavanjem u jednadžbu daje istinitu brojevnu jednakost.
Dvije su jednadžbe ekvivalentne ako imaju isto rješenje. Naprimjer, ekvivalentne su jednadžbe i
Najjednostavniji je oblik kvadratne jednadžbe jednadžba oblika
pri čemu je
Primjer 1.
Koje su od sljedećih jednadžbi linearne, a koje kvadratne?
Koje su od sljedećih jednadžbi linearne, a koje kvadratne?
Pomoć:
Zadane jednadžbe napiši u najjednostavnijem ekvivalentnom obliku.
Koje su od sljedećih jednadžbi kvadratne?
Pomoć:
Zadane jednadžbe napišite u najjednostavnijem ekvivalentnom obliku.
Riješiti kvadratnu jednadžbu oblika znači odrediti racionalni broj koji, uvrštavanjem u jednadžbu, daje istinitu brojevnu jednakost.
Primjer 2.
Koji racionalni broj zadovoljava uvjet
Uvjet (jednadžbu) možemo pisati u obliku pa bi netko (brzopleto) mogao zaključiti da je jedino rješenje postavljene jednadžbe.
Sjetimo se da su kvadrati međusobno suprotnih brojeva jednaki, tj. da vrijedi i zato ta kvadratna jednadžba ima dva rješenja i
Možemo razmišljati i na drugi način.
Zadanu jednadžbu možemo shvatiti kao razliku kvadrata i napisati je u obliku umnoška zbroja i razlike istih članova, tj. sjetiti se da vrijedi
Tada vrijedi
Umnožak dvaju članova jednak je ako je barem jedan od njih jednak tj. ako vrijedi ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Riješite kvadratne jednadžbe i provjerite točnost rješenja.
a.
a.
Umnožak je jednak ako je barem jedan od faktora jednak tj. ako vrijedi ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Provjera:
b.
b.
Umnožak je jednak ako je barem jedan od faktora jednak tj. ako vrijedi ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Drugi način:
Umnožak je jednak ako je barem jedan od faktora jednak tj. ako vrijedi ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Provjera:
c.
c.
Umnožak je jednak ako je barem jedan od faktora jednak tj. ako vrijedi ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Provjera:
d.
d.
Umnožak je jednak ako je barem jedan od faktora jednak tj. ako vrijedi ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Provjera:
e.
e. Postupimo li na isti način kao u prethodnim primjerima jednadžbu
možemo pisati u obliku umnoška
Umnožak je jednak
ako je barem jedan od faktora jednak
tj. ako vrijedi
ili
Rješenje linearne jednadžbe je
Rješenje linearne jednadžbe je
Dakle, ta jednadžba ima dva međusobno jednaka rješenja (često kažemo da ima jedno dvostruko rješenje).
f.
f.
Naučili ste da zbroj kvadrata nije moguće napisati u obliku umnoška dvaju linearnih izraza.
S druge strane vrijedi , što je zahtjev koji ne zadovoljava ni jedan racionalni broj . (Ne zaboravite da je kvadrat svakoga racionalnog broja nenegativni racionalni broj.)
Zadana jednadžba nema rješenja u skupu racionalnih brojeva.
Promotrimo najjednostavniju kvadratnu jednadžbu oblika
Ako je onda ta jednadžba ima točno dva rješenja, i
Ako je onda ta jednadžba ima jedno dvostruko rješenje,
Ako je onda ta jednadžba nema rješenja (u dosad poznatim vam skupovima brojeva) jer ne postoji broj koji pomnožen sa samim sobom daje negativan rezultat.
Zadane jednadžbe napišite na papir u obliku umnoška pa odredite sve racionalne brojeve za koje vrijedi zadana jednakost.
Ova jednadžba ima dva međusobno jednaka rješenja.
Zadanim jednadžbama pridružite njihova rješenja.
|
|
i |
|
|
i |
|
|
i |
|
|
i |
Pomoć:
Zadane jednadžbe napišite u obliku pa riješi dobivene linearne jednadžbe.
Uvježbajte rješavanje kvadratne jednadžbe oblika Nakon što riješite zadanu jednadžbu, s pomoću interaktivnog programa provjerite svoje rješenje te postupak rješavanja.
Riješite kvadratne jednadžbe.
Umožak je jednak ako je barem jedan od faktora jednak
Iako rješavanje složenijih kvadratnih jednadžbi prelazi granice osnovne škole, i u osnovnoj je školi moguće rješavati neke od njih.
Pogledajte videozapis s rješavanjem dvaju primjera malo složenijih kvadratnih jednadžbi.
Primjer 3.
Primjenjujući razliku kvadrata, napišimo jednadžbu u obliku umnoška. Riješimo kvadratnu jednadžbu i provjerimo točnost rješenja jednadžbe
Umnožak je jednak nuli ako je barem jedan od faktora jednak nuli, tj. ako vrijedi
odakle je ili
odakle je
Provjera:
Napišite na papiru u obliku umnoška i riješite kvadratne jednadžbe.
Kvadratne jednadžbe razvrstajte prema „vrsti” rješenja.
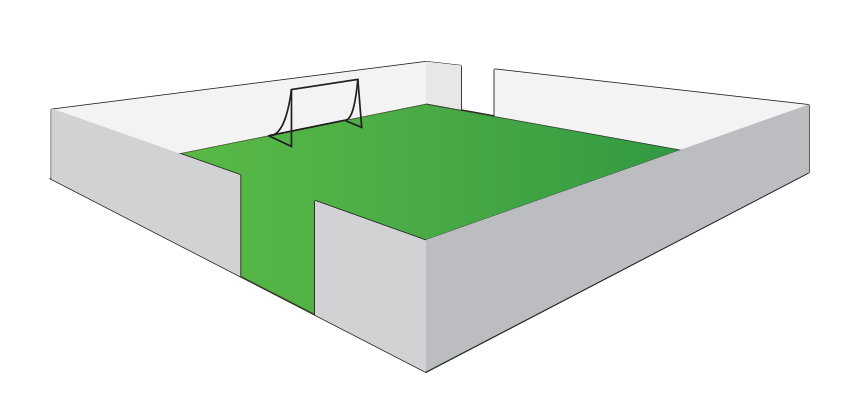
Igralište u oblika kvadrata ima površinu od kvadratnih metara. Oko igrališta treba postaviti ogradu, pri čemu na dva mjesta ostaju neograđeni dijelovi duljine metara za ulaz. Koliko metara ograde treba postaviti?
Ako je površina kvadrata sa stranicom dujine
jednaka
možemo pisati jednadžbu
Budući da je duljina stranice kvadrata pozitivan broj, rješavanjem te kvadratne jednadžbe dobivamo da je pozitivno rješenje te jednadžbe
Opseg tog kvadrata je
a ogradu je potrebno postaviti na
Ako neki predmet ispustimo iz ruke, brzina kojom tijelo pada stalno se povećava. Zanemarimo li otpor zraka, visina predmeta može se izračunati prema modelu:
pri čemu
predstavlja gravitacijsku konstantu s približnom vrijednošću
vertikalni položaj u metrima, a
vrijeme pada izraženo u sekundama. Koliko će vremena proći dok predmet ne padne na tlo ako je:
Uvrštavanjem podataka i u izraz dobivamo:
tj.
Budući da rješenje mora biti pozitivan broj, u obzir uzimamo samo pozitivno rješenje jednadžbe te zaključujemo da je sekunde.
Uvrštavanjem podataka i u izraz dobivamo:
tj.
Budući da rješenje mora biti pozitivan broj, u obzir uzimamo samo pozitivno rješenje jednadžbe te zaključujemo da je sekunda.
Energija koju ima tijelo u gibanju naziva se kinetička energija. Kinetičku energiju tijela računamo prema formuli pri čemu je masa tijela u kilogramima, a brzina tijela u metrima po sekundi. Mjerna jedinica za energiju je džul (oznaka ).
Tijelo mase kreće se i ima energiju od Kolikom se brzinom kreće to tijelo?
Uvrstimo li zadane podatke u formulu za kinetičku energiju, dobit ćemo:
Nakon sređivanja dobivamo redom:
Kvadratna jednadžba ili ima dva rješenja, no negativno rješenje nema smisla.
Tijelo se giba brzinom od metra u sekundi.
Tijelo mase
kreće se nepoznatom brzinom i ima energiju od
Kolikom se brzinom kreće?
Pomoć:
Kinetičku energiju tijela računamo prema formuli
Postupak:
Uvrštavanjem zadanih podataka u izraz
dobivamo
odnosno
Uvjet zadovoljavaju brojevi i no brzina je gibanja izražena pozitivnim brojem.
Kvadratne jednadžbe rješavali su još u starom Babilonu.
Starogrčki matematičari kvadratne su jednadžbe rješavali konstruktivno. Posebno su se isticali Euklid (3. st. pr. Krista) i Hiparh (2. st. pr. Krista). U računskom rješavanju povijest bilježi doprinos Diofanta i Herona.
Prvu opću formulu za rješavanje kvadratnih jednadžbi dao je Brahmagupta (Indija, 7. st.), dok Bombelli (16. st.) i Girard (17. st.) poznaju postupak rješavanja koji se i danas koristi.

Zlatni rez
Točka dijeli dužinu u omjeru zlatnog reza ako vrijedi
Označimo li
i
onda je
pa omjer zlatnog reza možemo zapisati kao
Taj se razmjer svodi na kvadratnu jednadžbu
Pogledajte interakciju u kojoj je prikazan postupak konstrukcije točke koja nactranu dužinu dijeli u omjeru zlatnog reza.
Na slici je prikazana zlatna spirala.
Pojam zlatnog reza (božanske proporcije) pripisuje se Pitagorejcima, a javlja se u prirodi, umjetnosti, arhitekturi...
Najpoznatija slika Leonarda da Vincija, Mona Lisa, primjer je primjene zlatnog reza u umjetnosti.U ovoj ste jedinici naučili:
Koristeći se stečenim znanje riješite zadatak.
Duljina je pravokutnika
veća od njegove širine. Površina je tog pravokutnika
Koliki je opseg tog pravokutnika?
Uputa: Pomoć u rješavanju možete pronaći u videoisječku u kojem je pokazano kako se rješava jednadžba
Zadatak je moguće rješavati na više načina. Jedan je način da postavimo i riješimo kvadratnu jednadžbu na način prikazan u videoisječku.
Prema uvjetu zadatka, ako s označimo širinu, onda je duljina označena s Vrijedi jednadžba
Lijevu stranu jednadžbe dopunimo na potpun kvadrat:
Dalje je:
Ova kvadratna jednadžba ima dva rješenja, ali negativno rješenje nema smisla.
Duljine su stranica tog pravokutnika i
Opseg je tog pravokutnika
Drugi način je mnogo jednostavniji i u rješavanju se koriste znanja prikazivanja složenog prirodnog broja u obliku umnoška (prirodnih brojeva). Konkretno, u zadatku je potrebno odrediti dva pozitivna (prirodna!) broja koji se razlikuju za
a koji pomnoženi daju
Jedini takvi brojevi su
i
pa zaključujemo da su duljine stranica tog pravokutnika
i
Jednadžbi pridruži njezin najjednostavniji ekvivalentni oblik.
|
|
|
|
|
|
|
|
|
|
|
Razvrstajte jednadžbe.
Pomoć:
Jednadžbe napišite u najjednostavnijem ekvivalentnom obliku.
Koji su od brojeva rješenje kvadratne jednadžbe
Pomoć:
Jednadžbu napišite u obliku razlike kvadrata, a zatim u obliku umnoška.
Postupak:
Kvadratnim jednadžbama pridružite rješenja.
|
|
|
|
|
|
|
|
|
|
|
|
Zbroj kvadrata triju uzastopnih neparnih prirodnih brojeva iznosi
Najmanji je od tih brojeva broj
Pomoć:
Ako je srednji od traženih brojeva, najmanji je a najveći
Uvjet zadatka možemo pisati u obliku jednadžbe
Postupak:
ili
Budući da tražimo prirodne brojeve, negativno rješenje odbacujemo i zaključujemo da je srednji broj Najmanji je a najveći
Provjerite da je.