

Utvrdite svoja znanja o potencijama broja i proširite ih na potencije drugih brojeva.
Neki od zadataka i aktivnosti koje slijede nešto su zahtjevniji i možda će vam biti potrebna mala pomoć u rješavanju. Nakon što riješite zadatak, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili ih zamolite da vam pomognu ako vam je neki zadatak i dalje nejasan
Primjenjujući stečena znanja o računanju s potencijama s bazom
riješite sljedećih devet zadataka.
Redne brojeve zadataka zamijenite pridruženim slovima i dobit ćete ime poznatog grčkog matematičara i njegovu još poznatiju izreku.
Riješite sve zadatke.
Odaberite odgovor koji smatrate točnim i obojit će se odgovarajući dio slike.
Flota Dunavskog Lloyda sastoji se od plovila različite nosivosti. Nosivost je plovila PZ17402 , a nosivost je plovila PO8506 . Za koliko je nosivost plovila PO8506 manja od nosivosti plovila PZ17402?
Atom ugljika sadrži protona, neutrona i elektrona. Jezgra atoma ugljika sadrži protona i neutrona. Masa je šest protona masa šest neutrona a masa šest elektrona
Masa je atoma ugljika
Potencija je broja umnožak broja sa samim sobom.
Ako je neki prirodni broj, onda je .
Potenciju broja
dovucite na odgovarajuće mjesto kako bi odgovarala vrijednost jednakosti.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
-ta potencija broja
je umnožak
faktora jednakih broju
Potenciju broja
dovucite na odgovarajuće mjesto kako bi odgovarala vrijednost jednakosti.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uočavate li neku pravilnost?
Kojom znamenkom završavaju brojevi
Prema kojemu se pravilu određuje posljednja znamenka potencije broja
Potencije broja završavaju znamenkom ili
Znamenke se ciklički ponavljaju ( , , , , , , , ...), tj. brojevi završavaju znamenkom . Znamenkom završavaju i ostale potencije broja čiji eksponent pri dijeljenju brojem daje ostatak
završavaju znamenkom . Znamenkom završavaju i ostale potencije broja čiji eksponent pri dijeljenju brojem daje ostatak .
završavaju znamenkom . Znamenkom završavaju i ostale potencije broja čiji eksponent pri dijeljenju brojem daje ostatak
završavaju znamenkom . Znamenkom završavaju i ostale potencije broja čiji je eksponent djeljiv brojem .
Broj završava znamenkom , a znamenkom .
Budući da broj pri dijeljenju s daje ostatak , broj završava znamenkom .
Budući da broj pri dijeljenju s daje ostatak , broj završava znamenkom .
Budući da broj pri dijeljenju s daje ostatak broj završava znamenkom
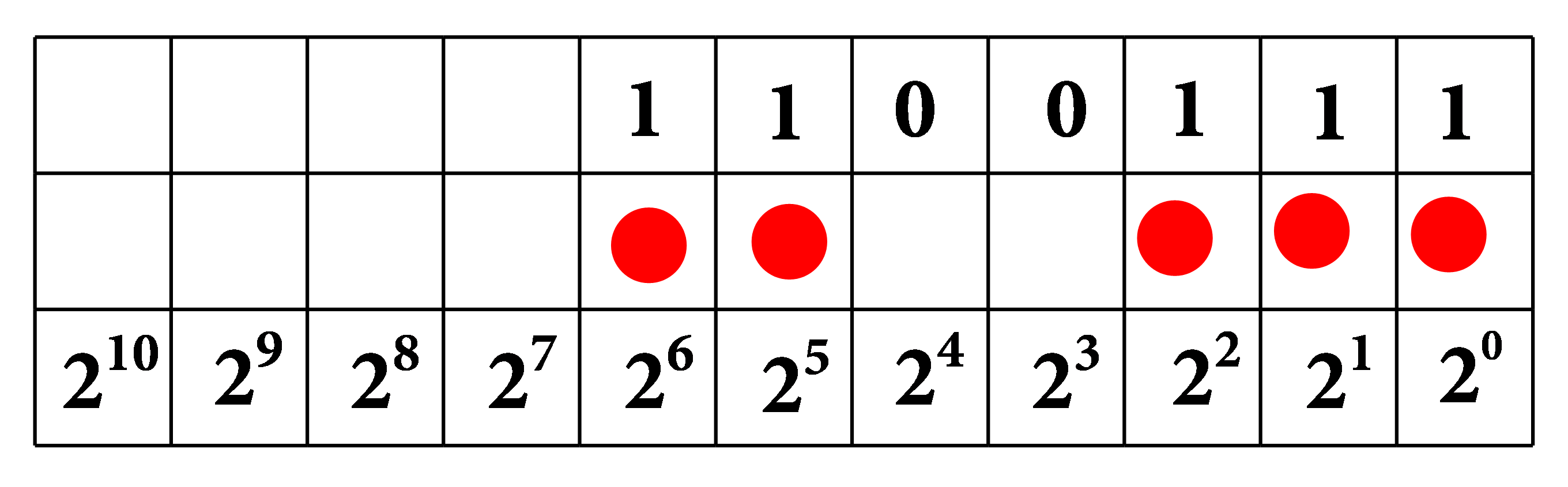
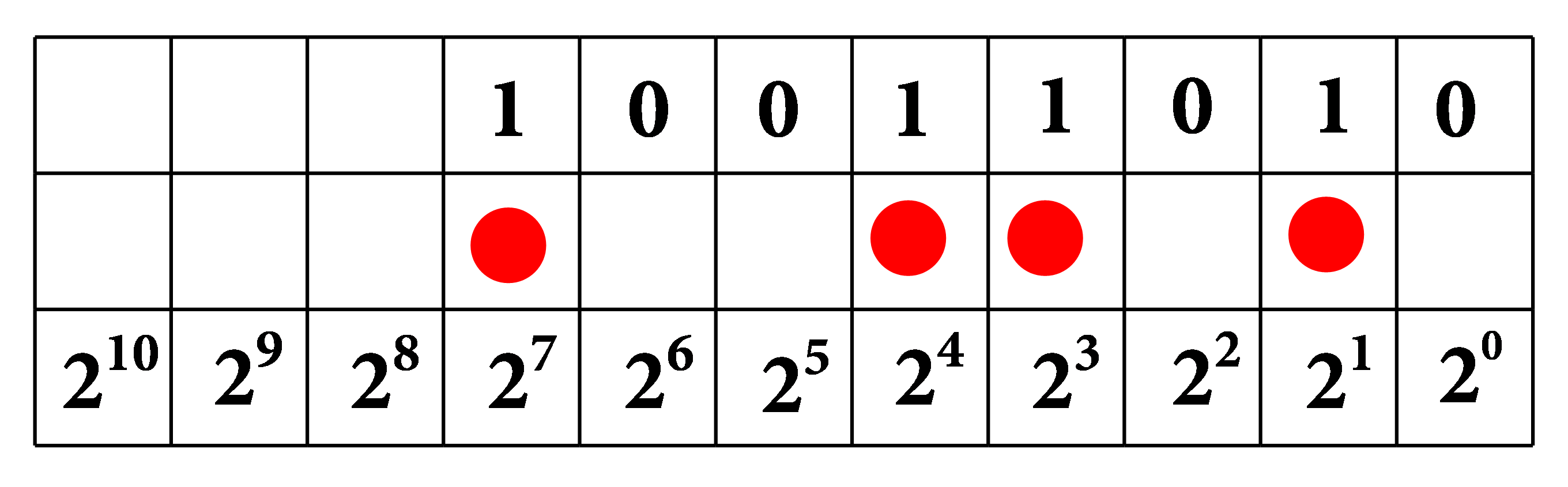
U informatici se koristi tzv. binarni brojevni sustav (sustav s bazom ), pri čemu se brojevi pišu kao nizovi nula i jedinica. Primjerice,
broj u binarnom sustavu predstavlja zapis broja
a broj
u binarnom sustavu predstavlja zapis broja
Obratan postupak - prevođenje broja između i iz dekadskog u binarni zapis možete proučiti uz pomoć interakcije.
Općenito, ako je i onda broj nazivamo -ta potencija broja
Pritom vrijedi:
Prikaz broja
Prikaz broja

Prikaz broja
Uz pomoć džepnog računala izračunajte i na crte upišite odgovarajuće vrijednosti.
Svi su rezultati objedinjeni u tablici koja slijedi:
| Potencija broja | Vrijednost potencije broja |
|---|---|
Primjećujete li neku pravilnost vezanu uz posljednju znamenku potencija broja
Potencije broja
(ciklički) završavaju redom znamenkama
Pravilo za određivanje posljednje znamenke potencije broja analogno je pravilu za određivanje posljednje znamenke broja Pokušajte ga izreći.
Koristeći džepno računalo, istražite postoji li pravilnost za određivanje posljednje znamenke -te potencije brojeva i
Svaka potencija broja jednaka je
Svaka potencija broja jednaka je
Potencije broja naizmjenično završavaju znamenkom (za neparne eksponente) ili znamenkom (za parne eksponente).
Svaka potencija broja završava znamenkom
Svaka potencija broja završava znamenkom
Potencije broja ciklički završavaju znamenkama ili
Potencije broja ciklički završavaju znamenkama ili
Potencije broja
naizmjenično završavaju znamenkom
ili znamenkom
Primjer 1.
Promotrimo niz potencija brojeva i
Uočavate li neku pravilnost vezanu za predznak rezultata?
Opišite uočenu pravilnost i provjerite vrijedi li i za potencije broja
s negativnim eksponentom.
Ako je eksponent potencije s negativnom bazom parni broj, potencija je pozitivna.
Ako je eksponent potencije s negativnom bazom neparni broj, potencija je negativna.
Uočena pravilnost vrijedi i za potencije broja s negativnim eksponentom.
U tablici su navedene dimenzije papira za formate od B0 do B10.
| Format | Dimenzije u mm |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Označite početnu duljinu papira formata s te širinu s Formulom izrazite duljinu i širinu papira formata u ovisnosti o broju Rezultat izrazite i zapišite na papir koristeći potencije.
Ako je parni broj ( , ), onda je i
Ako je neparni broj ( , ), onda je i
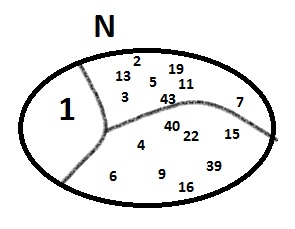
Prirodne brojeve možemo podijeliti u skupine prema djeljivosti na proste, složene i broj 1 koji nije ni prost ni složen.
Prosti brojevi imaju točno dva djelitelja, broj
i samog sebe.
Složeni brojevi imaju barem tri djelitelja.
Svaki složeni broj možemo na jedinstven način rastaviti na proste faktore.
Primjer 2.
Rastavimo broj na proste faktore.
Znamo da uzastopni umnožak istih faktora možemo zapisati potencijom.
Odredimo sve djelitelje broja i prebrojimo koliko ih ima.
Djelitelji su broja Ima ih osam.
Proučimo zapis rastava na proste faktore broja
:
U zapisu se pojavljuju eksponenti i
Uvećajmo svaki od njih za jedan i pomnožimo ih:
Primjer 3.
Odredimo koliko djelitelja ima broj
Samo je jedan eksponent u zapisu rastava,
Broj ima djelitelja.
Ispišimo ih:
Ako želimo odrediti broj djelitelja nekog broja, rastavimo ga na proste faktore i rastav zapišemo u obliku potencije. Svaki eksponent uvećamo za jedan i rezultate pomnožimo. Rezultat odgovara broju djelitelja.
Odredite broj djelitelja za zadane prirodne brojeve. Pokušajte ispisati sve djelitelje.
Postupak:
Postupak:
Postupak:
Primjer 4.
Poštanski su sandučići u jednom naselju zaštićeni troznamenkastim PIN-om. Koliko najviše sandučića može biti postavljeno ako svaki od njih mora imati drukčiji PIN?
Znamenke su:
Takvih PIN-ova ima
U tom naselju može biti najviše poštanskih sandučića.

Lokot sa zaporkom za bicikl ima četiri niza koluta s brojevima od do
Samo jedan niz daje kombinaciju koja otvara lokot.
Kolika je vjerojatnost pogađanja šifre iz prvog pokušaja?
Na raspolaganju imamo osam brojeva, od do
Broj svih mogućnosti je
Samo je jedna zaporka ona koja otvara lokot.
Neka je:
A - događaj otvaranja lokota
P(A) je vjerojatnost da će se lokot od prve otvoriti.
Vjerojatnost pogađanja šifre iz prvog pokušaja iznosi
To znači da bi se trebalo izvršiti različitih pokušaja kako bi jedan bio dobitni.
Izračunajte i upišite rješenje.
Postupak:
Pomoć:
Postupak:
Postupak:
Naučeno o potencijama možete dodatno uvježbati igricama Potencije - Memory i Znanstveni - Memory.
Članak Ivice Gusića objavljen u časopisu Matka, broj
(lipanj 1994.) sadrži zanimljive zadatke za vas.
Zabavite se!
Iz Rhindova papirusa
(Egipat, prije više od 3500 godina)
Jedan zadatak iz Rhindova papirusa može se shvatiti na ovaj način:
Na imanju je bilo sedam kuća. U svakoj je kući bilo sedam mačaka. Svaka mačka pojede po sedam miševa. Svaki bi miš pojeo po sedam klasova ječma.
Iz svakog bi klasa ječma izniklo po sedam pregršti ječma. Koliko su ječma mačke spasile?
U mnogih je naroda taj zadatak poprimio oblik pjesmice.
Navodimo dva takva primjera.
ENGLESKA DJEČJA BROJALICA (18. st.)
As I was going to St. Ives
I met a man with seven wives.
Every wife had seven sacks,
Every sack had seven cats,
Every cat had seven kits.
Kits, cats, sacks, wives,
How many were going to St. Ives?
BRANJE BRINJA
Kad sam išao brinje brati,
Kraj mene prođoše čudni svati.
Mladoženja se žalosno klimao,
Sedam je žena, jadnik imao.
Svaka je bila od njega veća,
Svaka je nosila po sedam vreća.
Vreće su bile od kozje dlake,
Sedam je mačaka mijaukalo iz svake.
I nijedna mačka nije ispala,
A svaka je po sedam mačića imala.
Mačići, mačke, vreće i žene!
Koliko nogu je prošlo kraj mene?