


Promotrite niz zaokruženih brojeva.
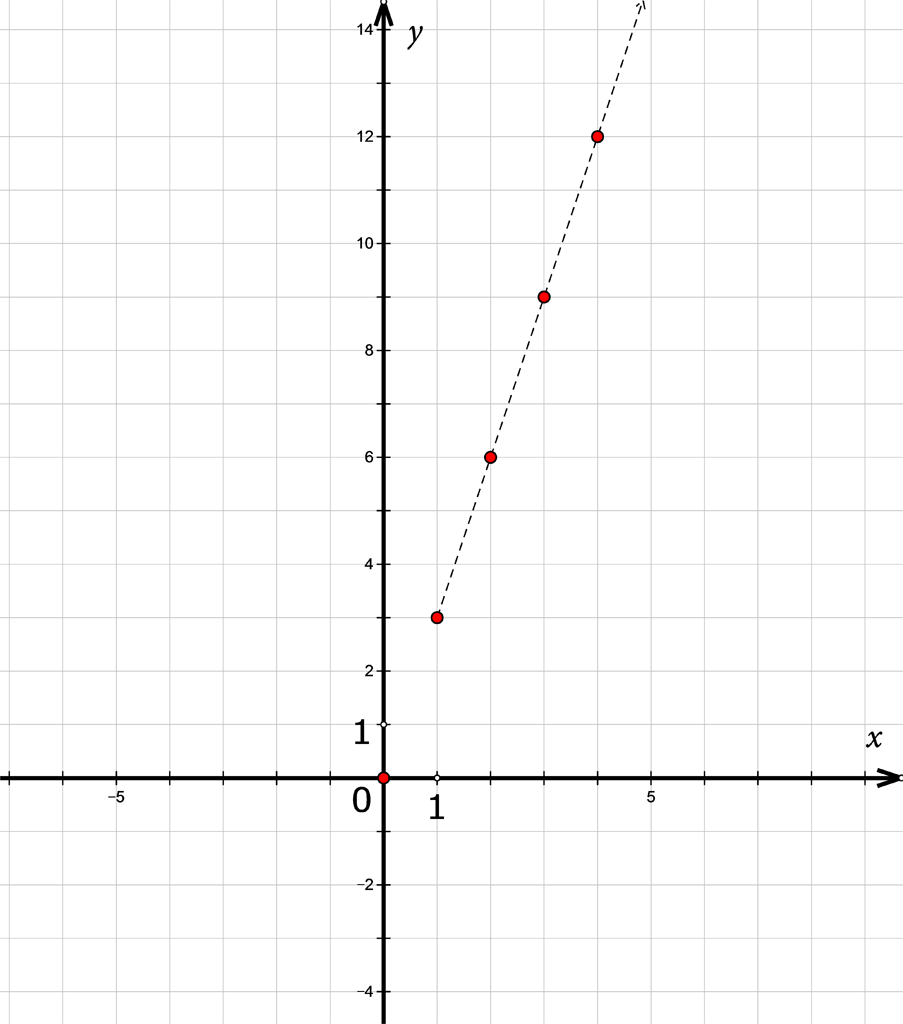
Funkcija u ovom kontekstu ima smisla za prirodne brojeve.
Početni zadatak opisuje linearnu ovisnost između rednog broja člana niza i njegove vrijednosti. Takve ovisnosti proučavane su u sedmom razredu.
Pod pojmom funkcija mislimo na način (pravilo) prema kojemu se svakom elementu jednog skupa pridružuje točno jedan, odgovarajući, element drugog skupa.
Ako su
realni brojevi
, pri čemu je
onda funkciju zadanu pravilom pridruživanja (formulom)
nazivamo linearnom funkcijom (na skupu
Graf je linearne funkcije
zadane pravilom pridruživanja
pravac s jednadžbom
Tom pravcu pripadaju sve točke pridružene uređenim parovima oblika
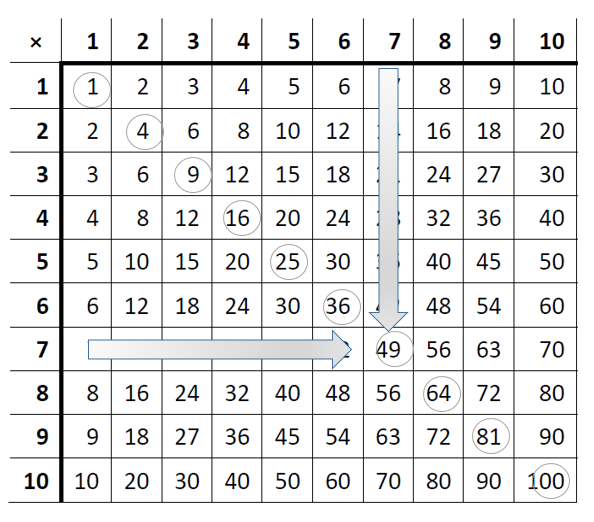
Promotrite niz zaokruženih brojeva.
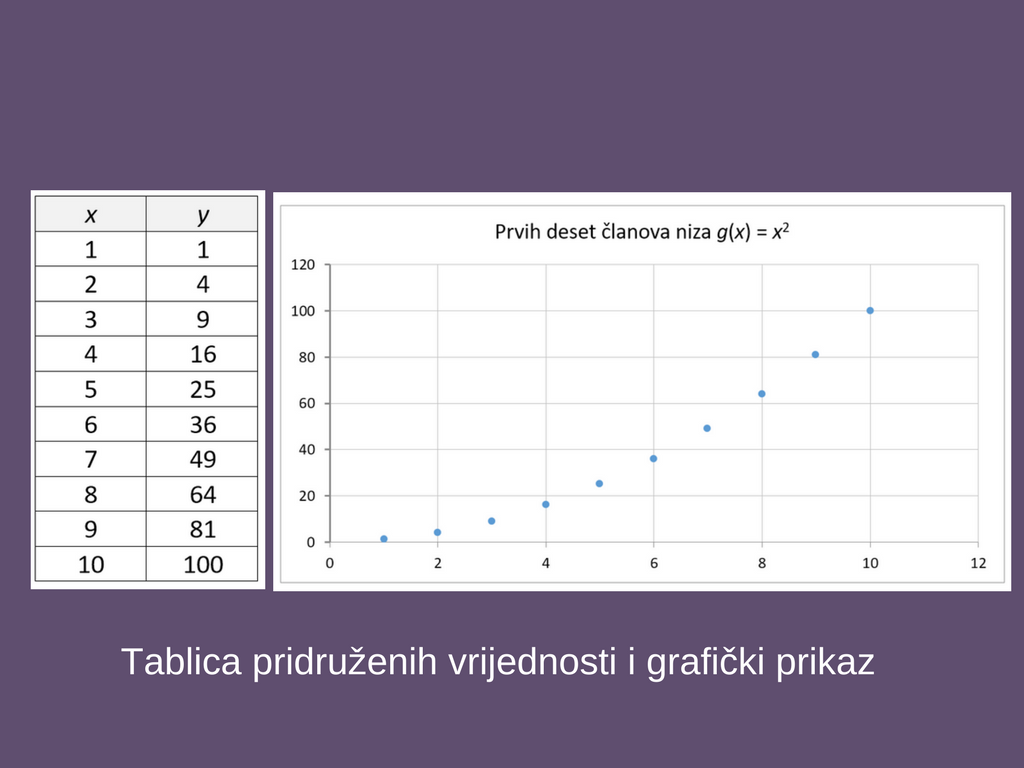
Kako bi izgledao graf funkcije koja svakom realnom broju pridružuje njegov kvadrat?
Na papir (u bilježnici) nacrtajte i popunite tablicu pridruženih vrijednosti te nacrtajte graf funkcije
|
|
|
|
||||||
Tablica:
|
|
|
|
||||||
Graf funkcije možete crtati i s pomoću online aplikacije na sljedećoj poveznici. Ako rabite online aplikaciju za crtanje, trebate u polje za upis unijeti uređene parove brojeva, jedan po jedan.
Graf:
Ako su
realni brojevi, pri čemu je
onda funkciju zadanu pravilom pridruživanja (formulom)
nazivamo (općom) kvadratnom funkcijom (na skupu
). Broj
naziva se argument funkcije, dok je
vrijednost funkcije za argument
Brojeve
nazivamo koeficijentima kvadratne funkcije.
Graf je kvadratne funkcije parabola s jednadžbom
Primjer 1.
Pomicanjem klizača poigrajte se grafičkim prikazom opće kvadratne funkcije.
U sljedećim videosadržajima pogledajte primjere parabola u svijetu koji nas okružuje te u videoigrici Super Mario. A svakako pogledajte i vodenu parabolu u Splitu.
U nastavku ćemo proučavati samo posebne slučajeve kvadratne funkcije, one zadane pravilom pridruživanja oblika pri čemu su realni brojevi,
Kvadratna funkcija
zadana je pravilom pridruživanja
Izračunajte vrijednost funkcije
za vrijednost argumenta.
Za kvadratnu funkciju zadanu pravilom pridruživanja nacrtajte na papiru i popunite tablicu pridruženih vrijednosti.
|
|
|
|
|
|
Graf je funkcije koja svakom realnom broju pridružuje točno jedan realan broj zadane pravilom pridruživanja krivulja koja se naziva parabola.
Činjenicu da funkcija svakom realnom broju pridružuje točno jedan realan broj kraće zapisujemo simbolički kao
Primjer 2.
- Napišimo na papir pravilo pridruživanja funkcije koja duljini polumjera kruga pridružuje površinu tog kruga.
- Nacrtajmo graf te funkcije ako je
- Za koje vrijednosti argumenta funkcija ima smisla?
- Kojem skupu brojeva pripadaju vrijednosti te funkcije?
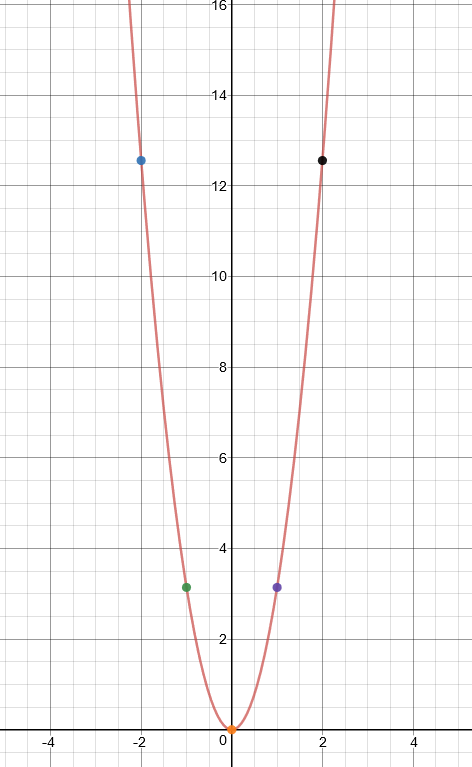
Vrijednosti funkcije pripadaju skupu nenegativnih realnih brojeva.
Primjer 3.
U istom pravokutnom koordinatnom sustavu u ravnini nacrtajmo grafove funkcija zadanih pravilima pridruživanja i Što možemo zamijetiti?
Uređene parove odnosno uputno je prije crtanja upisati u tablicu pridruženih vrijednosti.
Graf:
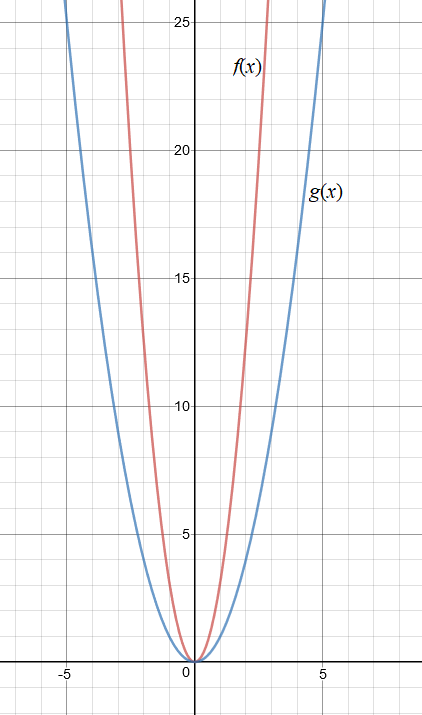
Grafovi su obiju funkcija parabole, pri čemu je graf funkcije „uži” od grafa funkcije
Što mislite, gdje će se u odnosu prema grafovima dviju funkcija iz prethodnog zadatka nalaziti graf funkcije zadane pravilom pridruživanja a gdje graf funkcije zadane pravilom pridruživanja Nacrtajte na papir grafove svih četiriju funkcija u istome pravokutnome koordinatnom sustavu u ravnini. Što zamjećujete?
Tablica:
Prije crtanja grafova dopunimo tablicu pridruženih vrijednosti za kvadratne funkcije zadane pravilima pridruživanja i
Graf:
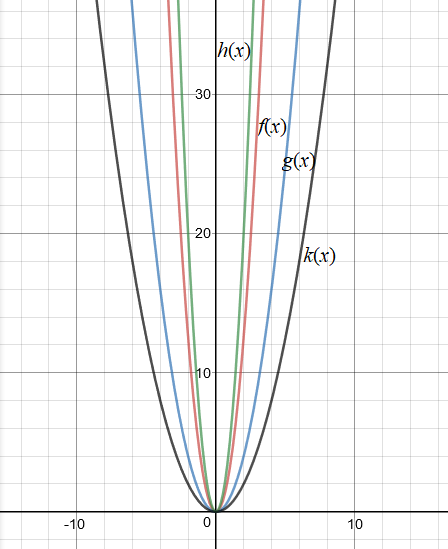
Provjerite navedene tvrdnje s pomoću GeoGebrine interakcije.
Mijenjajte vrijednost parametra . Istražite ovisnost vrijednosti funkcije , odnosno izgleda grafa te funkcije o vrijednosti parametra ( ).
Primjer 4.
Kako bi izgledao graf kvadratne funkcije zadane pravilom pridruživanja koju dobijemo množenjem broja proizvoljnim koeficijentom
U istome koordinatnom sustavu u ravnini prikažimo:
Što možemo zamijetiti?
Prije crtanja, popunit ćemo tablicu pridruženih vrijednosti.
Graf:
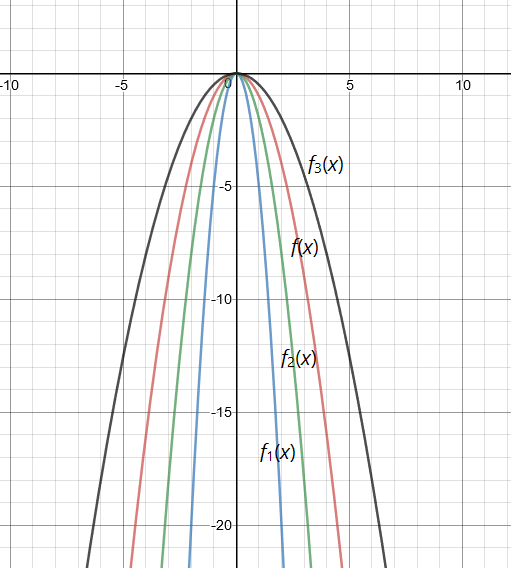
Na temelju nacrtanih grafova zaključujemo:
Provjerite navedene tvrdnje s pomoću GeoGebrine interakcije.
Mijenjajte vrijednost parametra Istražite ovisnost vrijednosti funkcije , odnosno izgleda grafa te funkcije o vrijednosti parametra ( ).
Provjerimo razumijevanje.
Ako je vijednost parametra
kvadratne funkcije oblika
pozitivna, onda će parabola biti okrenuta prema gore.
Što je apsolutna vrijednost parametra
kvadratne funkcije oblika
veća, to je graf te funkcije „uži”.
Grafički je prikaz linearne funkcije parabola.
Grafovi kvadratne funkcije oblika
simetrični su s obzirom na os
Postupak crtanja parabola možete još jedanput proučiti i s pomoću GeoGebrine interakcije.
Pripada li točka s koordinatama (
) grafu funkcije
zadane pravilom pridruživanja
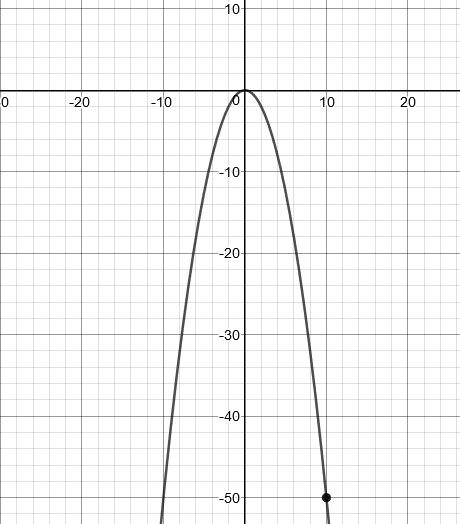
Prvi je način rješavanja algebarski.
Drugi je način grafički. Nacrtajmo graf funkcije te provjerimo pripada li zadana točka paraboli.
U oba slučaja vidimo da točka s koordinatama ( ) pripada grafu funkcije zadane pravilom pridruživanja
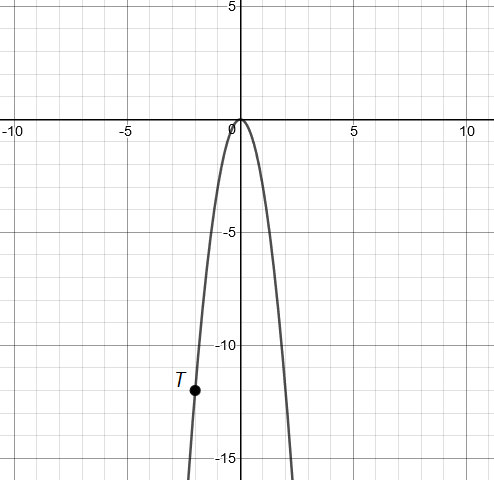
Očitajte koordinate točke koja pripada grafu neke kvadratne funkcije Kakvog je predznaka parametar ?
Budući da je parabola okrenuta prema dolje, parametar je negativan.
U nastavku ćemo se pozabaviti složenijim oblicima kvadratne funkcije. Za početak to je...
Kvadratna funkcija zadana je pravilom pridruživanja Odredite vrijednost funkcije za vrijednost argumenta:
Uvrštavanjem dobivamo:
Primjer 5.
U istom koordinatnom sustavu nacrtajmo grafove kvadratnih funkcija , i zadanih pravilima pridruživanja
Za svaku funkciju prvo treba popuniti tablicu pridruženih vrijednosti, na temelju tablice formirati uređene parove, i na kraju uređene parove ucrtati u pravokutni koordinatni sustav.
Graf:
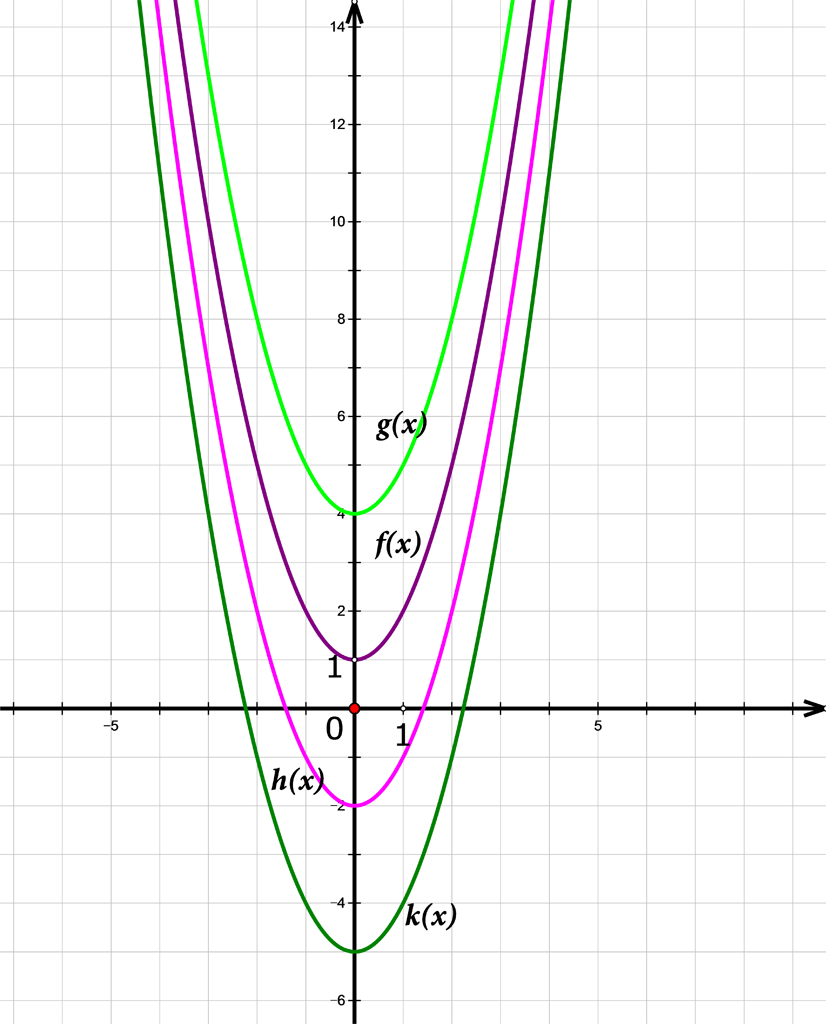
Uočite:
Graf kvadratne funkcije zadane pravilom pridruživanja dobivamo pomakom grafa osnovne kvadratne funkcije zadane pravilom pridruživanja duž osi za vrijednost parametra .
Pomicanjem klizača istražite što se događa s grafom kvadratne funkcije zadane pravilom pridruživanja u odnosu prema grafu kvadratne funkcije zadane sa
Kvadratna funkcija zadana je pravilom pridruživanja
Odredite vrijednost funkcije
za vrijednost argumenta:
Uvrštavanjem dobivamo:
Primjer 6.
U istome koordinatnom sustavu nacrtajmo grafove kvadratnih funkcija i zadanih pravilima pridruživanja i
Za svaku funkciju prvo treba popuniti tablicu pridruženih vrijednosti, na temelju tablice formirati uređene parove i na kraju uređene parove ucrtati u pravokutni koordinatni sustav.
Graf:
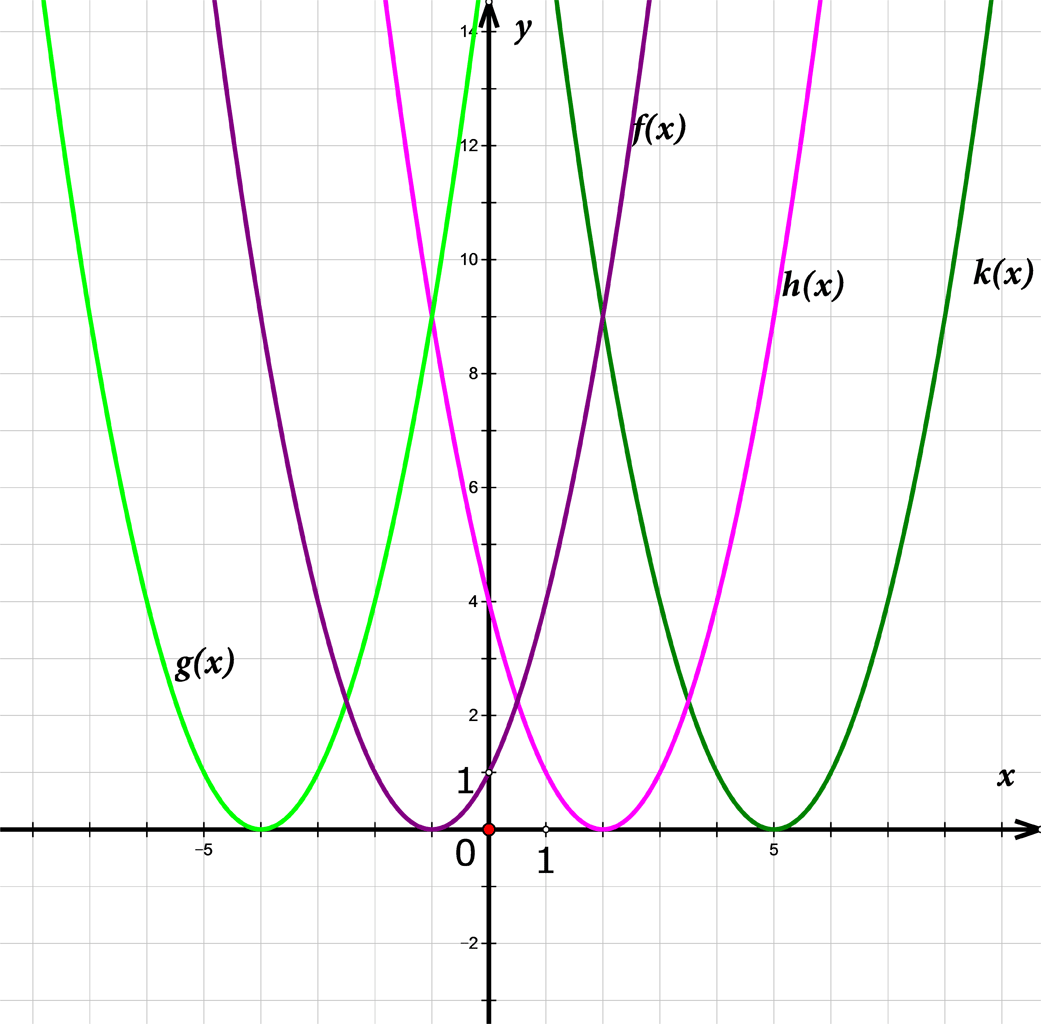
Uočite da vrijede svojstva:
Graf kvadratne funkcije zadane pravilom pridruživanja dobivamo pomakom grafa osnovne kvadratne funkcije zadane pravilom pridruživanja duž osi za suprotnu vrijednost parametra
Pomicanjem klizača istražite što se događa s grafom kvadratne funkcije zadane pravilom pridruživanja u odnosu prema grafu kvadratne funkcije zadane sa
Odredite ordinatu točke s apscisom koja pripada grafu funkcije zadane pravilom pridruživanja
Tražena točka je pridružena uređenom paru oblika ( ), pri čemu je
Odredite apscisu točke s ordinatom koja pripada grafu funkcije zadane pravilom pridruživanja
Tražena je točka pridružena uređenom paru oblika (
), pri čemu je
Iz
slijedi da je
ili
Kolika je vrijednost koeficijenta
funkcije
zadane pravilom pridruživanja
ako točka
pripada grafu te funkcije?
Uvjete zadatka možemo zapisati u obliku
tj.
odakle je
Kolika je vrijednost koeficijenta
kvadratne funkcije
zadane pravilom pridruživanja
ako točka
pripada grafu te funkcije?
Uvjete zadatka možemo zapisati u obliku odakle je redom
i konačno
Koja je najmanja moguća vrijednost funkcije zadane pravilom pridruživanja Nacrtajtena papiru graf te funkcije te objasnite svoj odgovor.
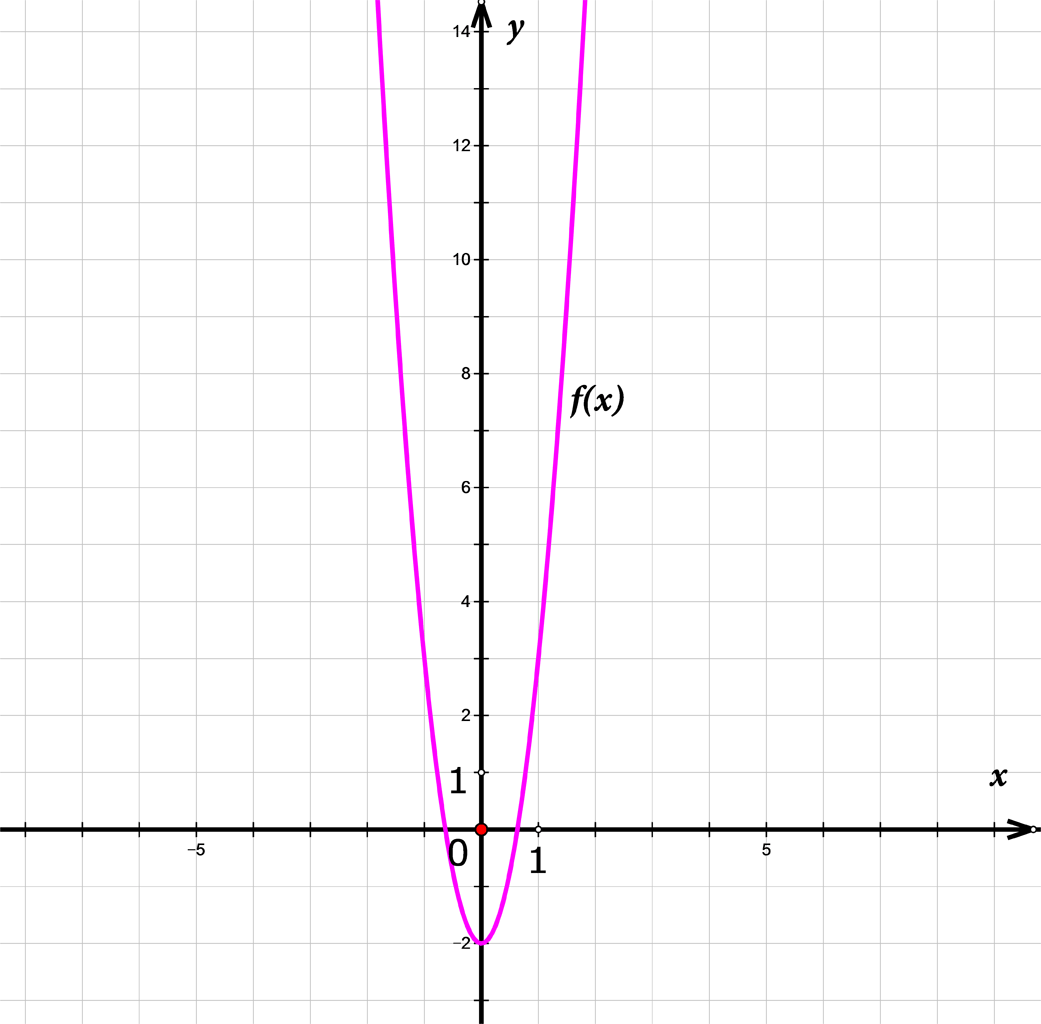
Najniža je točka grafa ove funkcije
Zaključujemo da je najmanja moguća vrijednost zadane funkcije jednaka
a tu vrijednost funkcija poprima za

Naučili ste iskazati ovisnost dviju veličina riječima i tablicom pridruženih vrijednosti, nacrtati graf funkcije
ispitati pripadnost točke grafu funkcije
te očitati koordinatu točke koja pripada grafu kvadratne funkcije. Koristeći se stečenim znanjem, riješite zadatak.
Na slici je graf kvadratne funkcije zadane pravilom pridruživanja Koristeći se nacrtanim grafom, odredite ordinate točaka i apscise točaka i
Odredite pravilo pridruživanja funkcije pa računski provjerite pripada li točka grafu nacrtane funkcije.
što znači da točka s koordinatama ne pripada grafu te funkcije.
Za kraj, možete procijeniti svoje znanje.
Ako želite, možete istražiti što se događa s grafom kvadratne funkcije zadane pravilom pridruživanja
te istražiti kosi hitac.
S pomoću sljedeće animacije istražite kosi hitac te odgovorite na pitanje. Pod kojim kutom projektil treba biti izbačen kako bi postigao najveću udaljenost?
Kvadratna funkcija zadana je pravilom pridruživanja:
Zadani broj kvadriraj pa od rezultata oduzmi
Prema tom pravilu, broju
pridružen je broj
Pomoć:
Pravilo pridruživanja možemo napisati u obliku
Postupak:
Kvadratna funkcija zadana je pravilom pridruživanja Koje od točaka pripadaju grafu ove funkcije?
Kvadratna funkcija zadana je pravilom pridruživanja
Zadanim vrijednostima argumenta pridružite odgovarajuće vrijednosti funkcije
.
Kvadratne funkcije
i
zadane su pravilima pridruživanja
i
Kvadratne funkcije , i zadane su pravilima pridruživanja i Poredajte po veličini, počevši od najmanje, vrijednosti ovih funkcija za vrijednost argumenta